Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 10 SBT bài 1 chương 4

Bất đẳng thức

Toán 10 - Bất đẳng thức

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT bài 1 chương 4, tài liệu gồm 14 bài tập trang 106 kèm theo lời giải chi tiết sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán lớp 10 một cách hiệu quả hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT bài 1 chương 3

Giải bài tập Toán 10 SBT bài 2 chương 3

Giải bài tập Toán 10 SBT bài 3 chương 3

Giải bài tập Toán 10 SBT ôn tập chương 3

Giải bài tập Toán 10 SBT bài 1

Bài 1 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${x^4} + {y^4} \ge {x^3}y + x{y^3}$ ${x^4} + {y^4} \ge {x^3}y + x{y^3}$

Gợi ý làm bài

${x^4} + {y^4} \ge {x^3}y + x{y^3} \Leftrightarrow {x^4} + {y^4} - {x^3}y - x{y^3} \ge 0$ ${x^4} + {y^4} \ge {x^3}y + x{y^3} \Leftrightarrow {x^4} + {y^4} - {x^3}y - x{y^3} \ge 0$

$\Leftrightarrow {x^3}(x - y) + {y^3}(y - x) \ge 0 \Leftrightarrow (x - y)({x^3} - {y^3}) \ge 0$ $\Leftrightarrow {x^3}(x - y) + {y^3}(y - x) \ge 0 \Leftrightarrow (x - y)({x^3} - {y^3}) \ge 0$

$\Leftrightarrow {(x - y)^2}({x^2} + {y^2} + xy) \ge 0 \Leftrightarrow {(x - y)^2}({(x + {y \over 2})^2} + {{3{y^2}} \over 4}) \ge 0$ $\Leftrightarrow {(x - y)^2}({x^2} + {y^2} + xy) \ge 0 \Leftrightarrow {(x - y)^2}({(x + {y \over 2})^2} + {{3{y^2}} \over 4}) \ge 0$ (đúng)

Bài 2 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${x^2} + 4{y^2} + 3{z^2} + 14 > 2x + 12y + 6z$ ${x^2} + 4{y^2} + 3{z^2} + 14 > 2x + 12y + 6z$

Gợi ý làm bài

${x^2} + 4{y^2} + 3{z^2} + 14 > 2x + 12y + 6z$ ${x^2} + 4{y^2} + 3{z^2} + 14 > 2x + 12y + 6z$

$\Leftrightarrow {x^2} - 2x + 4{y^2} - 12y + 3({z^2} - 2z) + 14 > 0$ $\Leftrightarrow {x^2} - 2x + 4{y^2} - 12y + 3({z^2} - 2z) + 14 > 0$

$\Leftrightarrow {(x - 1)^2}{(2y - 3)^2} + 3{(z - 1)^2} + 1 > 0$ $\Leftrightarrow {(x - 1)^2}{(2y - 3)^2} + 3{(z - 1)^2} + 1 > 0$ (đúng)

Bài 3 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${a \over {\sqrt b }} + {b \over {\sqrt a }} \ge \sqrt a + \sqrt b$ ${a \over {\sqrt b }} + {b \over {\sqrt a }} \ge \sqrt a + \sqrt b$

Gợi ý làm bài

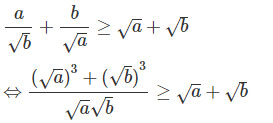
Giải bài tập Toán 10 SBT bài 1 chương 4

$\Leftrightarrow (\sqrt a + \sqrt b )(a + b - \sqrt {ab} ) \ge (\sqrt a + \sqrt b )\sqrt {ab}$ $\Leftrightarrow (\sqrt a + \sqrt b )(a + b - \sqrt {ab} ) \ge (\sqrt a + \sqrt b )\sqrt {ab}$

$\Leftrightarrow (\sqrt a + \sqrt b )(a + b - 2\sqrt {ab} ) \ge 0$ $\Leftrightarrow (\sqrt a + \sqrt b )(a + b - 2\sqrt {ab} ) \ge 0$

$\Leftrightarrow (\sqrt a + \sqrt b ){(\sqrt a - \sqrt b )^2} \ge 0$ $\Leftrightarrow (\sqrt a + \sqrt b ){(\sqrt a - \sqrt b )^2} \ge 0$ (đúng)

Bài 4 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${1 \over a} + {1 \over b} \ge {4 \over {a + b}}$ ${1 \over a} + {1 \over b} \ge {4 \over {a + b}}$

Gợi ý làm bài

Từ ${1 \over a} + {1 \over b} \ge 2\sqrt {{1 \over {ab}}}$ ${1 \over a} + {1 \over b} \ge 2\sqrt {{1 \over {ab}}}$ và $a + b \ge 2\sqrt {ab}$ $a + b \ge 2\sqrt {ab}$ suy ra

$(a + b)({1 \over a} + {1 \over b}) \ge 4$ $(a + b)({1 \over a} + {1 \over b}) \ge 4$ hay ${1 \over a} + {1 \over b} \ge {4 \over {a + b}}$ ${1 \over a} + {1 \over b} \ge {4 \over {a + b}}$

Bài 5 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${{a + b + c + d} \over 4}$ ${{a + b + c + d} \over 4}$ ≥ $\sqrt[4]{abcd}$ $\sqrt[4]{abcd}$

Gợi ý làm bài

Từ $a + b \ge 2\sqrt {ab}$ $a + b \ge 2\sqrt {ab}$ và $c + d \ge 2\sqrt {cd}$ $c + d \ge 2\sqrt {cd}$ suy ra

$a + b + c + d \ge 2(\sqrt {ab} + \sqrt {cd} )$ $a + b + c + d \ge 2(\sqrt {ab} + \sqrt {cd} )$

$= > 2.2\sqrt {\sqrt {ab} .\sqrt {cd} }$ $= > 2.2\sqrt {\sqrt {ab} .\sqrt {cd} }$

$=> {{a + b + c + d} \over 4}$ $=> {{a + b + c + d} \over 4}$ ≥ $\sqrt[4]{abcd}$ $\sqrt[4]{abcd}$

$=> a + b + c + d \ge 2.2\sqrt {\sqrt {ab} .\sqrt {cd} }$ $=> a + b + c + d \ge 2.2\sqrt {\sqrt {ab} .\sqrt {cd} }$

$=> {{a + b + c + d} \over 4}$ $=> {{a + b + c + d} \over 4}$ ≥ $\sqrt[4]{abcd}$ $\sqrt[4]{abcd}$

Bài 6 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge {{16} \over {a + b + c + d}}$ ${1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge {{16} \over {a + b + c + d}}$

Gợi ý làm bài

Từ $a + b + c + d \ge$ $a + b + c + d \ge$ $\sqrt[4]{abcd}$ $\sqrt[4]{abcd}$

${1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge$ ${1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge$ $4\sqrt[4]{\frac{1}{abcd}}$ $4\sqrt[4]{\frac{1}{abcd}}$

Suy ra $(a + b + c + d)({1 \over a} + {1 \over b} + {1 \over c} + {1 \over d}) \ge 16$ $(a + b + c + d)({1 \over a} + {1 \over b} + {1 \over c} + {1 \over d}) \ge 16$

Hay ${1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge {{16} \over {a + b + c + d}}$ ${1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge {{16} \over {a + b + c + d}}$

Bài 7 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${a^2}b + {1 \over b} \ge 2a$ ${a^2}b + {1 \over b} \ge 2a$

Gợi ý làm bài

${a^2}b + {1 \over b} \ge 2\sqrt {{a^2}b.{1 \over b}} = 2a$ ${a^2}b + {1 \over b} \ge 2\sqrt {{a^2}b.{1 \over b}} = 2a$

Bài 8 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$(a + b)(b + c)(c + a) \ge 8abc$ $(a + b)(b + c)(c + a) \ge 8abc$

Gợi ý làm bài

Từ $a + b \ge 2\sqrt {ab} ,b + c \ge 2\sqrt {bc} ,c + a \ge 2\sqrt {ca}$ $a + b \ge 2\sqrt {ab} ,b + c \ge 2\sqrt {bc} ,c + a \ge 2\sqrt {ca}$

Suy ra: $(a + b)(b + c)(c + a) \ge 8abc$ $(a + b)(b + c)(c + a) \ge 8abc$

Bài 9 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${(\sqrt a + \sqrt b )^2} \ge 2\sqrt {2(a + b)\sqrt {ab} }$ ${(\sqrt a + \sqrt b )^2} \ge 2\sqrt {2(a + b)\sqrt {ab} }$

Gợi ý làm bài

${(\sqrt a + \sqrt b )^2} = a + b + 2\sqrt {ab} \ge 2\sqrt {(a + b).2\sqrt {ab} }$ ${(\sqrt a + \sqrt b )^2} = a + b + 2\sqrt {ab} \ge 2\sqrt {(a + b).2\sqrt {ab} }$

Bài 10 trang 106 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${1 \over a} + {1 \over b} + {1 \over c} \ge {9 \over {a + b + c}}$ ${1 \over a} + {1 \over b} + {1 \over c} \ge {9 \over {a + b + c}}$

Gợi ý làm bài

$(a + b + c)({1 \over a} + {1 \over b} + {1 \over c}) = 1 + 1 + 1 + ({a \over b} + {b \over a}) + ({a \over c} + {c \over a}) + ({b \over c} + {c \over b})$ $(a + b + c)({1 \over a} + {1 \over b} + {1 \over c}) = 1 + 1 + 1 + ({a \over b} + {b \over a}) + ({a \over c} + {c \over a}) + ({b \over c} + {c \over b})$

$\ge 3 + 2 + 2 + 2 = 9 = > {1 \over a} + {1 \over b} + {1 \over c} \ge {9 \over {a + b + c}}$ $\ge 3 + 2 + 2 + 2 = 9 = > {1 \over a} + {1 \over b} + {1 \over c} \ge {9 \over {a + b + c}}$

Bài 11 trang 106 Sách bài tập (SBT) Toán Đại số 10

Tìm giá trị nhỏ nhất của hàm số

$y = {4 \over x} + {9 \over {1 - x}}$ $y = {4 \over x} + {9 \over {1 - x}}$ với 0 < x < 1.

Gợi ý làm bài

$y = {{4(x + 1 - x)} \over x} + {{9(x + 1 - x)} \over {1 - x}}$ $y = {{4(x + 1 - x)} \over x} + {{9(x + 1 - x)} \over {1 - x}}$

$=4 + 9 + {{4(1 - x)} \over x} + 9.{x \over {1 - x}} \ge 13 + 2\sqrt {4.{{(1 - x)} \over x}.9.{x \over {1 - x}}} = 25$ $=4 + 9 + {{4(1 - x)} \over x} + 9.{x \over {1 - x}} \ge 13 + 2\sqrt {4.{{(1 - x)} \over x}.9.{x \over {1 - x}}} = 25$

$=> y \ge 25,\forall x \in (0;1)$ $=> y \ge 25,\forall x \in (0;1)$

Đẳng thức y = 25 xảy ra khi và chỉ khi

$\left\{ \matrix{{{4(1 - x)} \over x} = {{9x} \over {1 - x}} = 6 \hfill \cr x \in (0;1) \hfill \cr} \right.$ $\left\{ \matrix{{{4(1 - x)} \over x} = {{9x} \over {1 - x}} = 6 \hfill \cr x \in (0;1) \hfill \cr} \right.$

hay $x = {2 \over 5}$ $x = {2 \over 5}$

Vậy giá trị nhỏ nhất của hàm số đã cho bằng 25 đạt tại $x = {2 \over 5}$ $x = {2 \over 5}$

Bài 12 trang 106 Sách bài tập (SBT) Toán Đại số 10

Tìm giá trị lớn nhất của hàm số

$y = 4{x^3} - {x^4}$ $y = 4{x^3} - {x^4}$ với $0 \le x \le 4$ $0 \le x \le 4$

Gợi ý làm bài

$y = 4{x^3} - {x^4} = {x^3}(4 - x)$ $y = 4{x^3} - {x^4} = {x^3}(4 - x)$

$=> 3y = x.x.x(12 - 3x) \le {({{x + x} \over 2})^2}{({{x + 12 - 3x} \over 2})^2}$ $=> 3y = x.x.x(12 - 3x) \le {({{x + x} \over 2})^2}{({{x + 12 - 3x} \over 2})^2}$

$= > 48 \le {{\rm{[}}2x(12 - 2x){\rm{]}}^2} \le {({{2x + 12 - 2x} \over 2})^4} = {6^4}$ $= > 48 \le {{\rm{[}}2x(12 - 2x){\rm{]}}^2} \le {({{2x + 12 - 2x} \over 2})^4} = {6^4}$

$= > y \le {{{6^4}} \over {48}} = 27,\forall x \in {\rm{[}}0;4]$ $= > y \le {{{6^4}} \over {48}} = 27,\forall x \in {\rm{[}}0;4]$

$y = 27 \Leftrightarrow \left\{ \matrix{x = x \hfill \cr x = 12 - 3x \hfill \cr 2x = 12 - x \hfill \cr x \in {\rm{[}}0;4] \hfill \cr} \right. \Leftrightarrow x = 3$ $y = 27 \Leftrightarrow \left\{ \matrix{x = x \hfill \cr x = 12 - 3x \hfill \cr 2x = 12 - x \hfill \cr x \in {\rm{[}}0;4] \hfill \cr} \right. \Leftrightarrow x = 3$

Vậy giá trị lớn nhất của hàm số đã cho bằng 27 đạt được khi x = 3.

Bài 13 trang 106 Sách bài tập (SBT) Toán Đại số 10

Tìm giá trị lớn nhất, nhỏ nhất của hàm số sau trên tập xác định của nó

$y = \sqrt {x - 1} + \sqrt {5 - x}$ $y = \sqrt {x - 1} + \sqrt {5 - x}$

Gợi ý làm bài

Vế phải có nghĩa khi $1 \le x \le 5$ $1 \le x \le 5$

Ta có: ${y^2} = {(\sqrt {x - 1} + \sqrt {5 - x} )^2} = 4 + 2\sqrt {(x - 1)(5 - x)}$ ${y^2} = {(\sqrt {x - 1} + \sqrt {5 - x} )^2} = 4 + 2\sqrt {(x - 1)(5 - x)}$

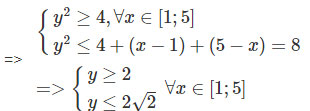
Giải bài tập Toán 10 SBT bài 1 chương 4

Hơn nữa $y = 2 \Leftrightarrow (x - 1)(5 - x) = 0 \Leftrightarrow \left[ \matrix{x = 1 \hfill \cr x = 5 \hfill \cr} \right.$$ $y = 2 \Leftrightarrow (x - 1)(5 - x) = 0 \Leftrightarrow \left[ \matrix{x = 1 \hfill \cr x = 5 \hfill \cr} \right.$$

$y = 2\sqrt 2 \Leftrightarrow x - 1 = 5 - x \Leftrightarrow x = 3$ $y = 2\sqrt 2 \Leftrightarrow x - 1 = 5 - x \Leftrightarrow x = 3$

Vậy giá trị lớn nhất của hàm số đã cho bằng $2\sqrt 2$ $2\sqrt 2$ khi x = 3, giá trị nhỏ nhất của hàm số đã cho bằng 2 khi x = 1 hoặc x = 5.

Bài 14 trang 106 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng:

$\left| {x - z} \right| \le \left| {x - y} \right| + \left| {y - z} \right|,\forall x,y,z$ $\left| {x - z} \right| \le \left| {x - y} \right| + \left| {y - z} \right|,\forall x,y,z$

Gợi ý làm bài

$\left| {x - z} \right| = \left| {(x - y) + (y - z)} \right| \le \left| {x - y} \right| + \left| {y - z} \right|$ $\left| {x - z} \right| = \left| {(x - y) + (y - z)} \right| \le \left| {x - y} \right| + \left| {y - z} \right|$

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

351