Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số bậc hai

Toán 10 - Hàm số bậc hai

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT bài 3 chương 2, tài liệu gồm 6 bài tập trang 40 kèm theo đáp án sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán 10 một cách hiệu quả hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT bài 5 chương 1

Giải bài tập Toán 10 SBT ôn tập chương 1

Giải bài tập Toán 10 SBT bài 1 chương 2

Giải bài tập Toán 10 SBT bài 2 chương 2

Giải bài tập Toán 10 SBT bài 3

Bài 14 trang 40 Sách bài tập (SBT) Toán Đại số 10

Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.

a) y=2x²−x−2

b) y=−2x²−x+2

c) $y = - {1 \over 2}{x^2} + 2x - 1$ $y = - {1 \over 2}{x^2} + 2x - 1$

d) $y = - {1 \over 2}{x^2} + 2x - 1$ $y = - {1 \over 2}{x^2} + 2x - 1$

Gợi ý làm bài

a) Ở đây $a = 2;b = - 2;c = - 2$. Ta có $\Delta = {( - 1)^2} - 4.2.( - 2) = 17$ $\Delta = {( - 1)^2} - 4.2.( - 2) = 17$

Trục đối xứng là đường thẳng $x = {1 \over 4}$ $x = {1 \over 4}$ ; đỉnh $I({1 \over 4}; - {{17} \over 8})$ $I({1 \over 4}; - {{17} \over 8})$ giao với trục tung tại điểm (0;-2).

Để tìm giao điểm với trục hoành ta giải phương trình

$2{x^2} - x - 2 = 0 \Leftrightarrow {x_{1,2}} = {{1 \pm \sqrt {17} } \over 4}$ $2{x^2} - x - 2 = 0 \Leftrightarrow {x_{1,2}} = {{1 \pm \sqrt {17} } \over 4}$

Vậy các giao điểm với trục hoành là $({{1 + \sqrt {17} } \over 4};0 )$ $({{1 + \sqrt {17} } \over 4};0 )$ và $({{1 - \sqrt {17} } \over 4};0 )$ $({{1 - \sqrt {17} } \over 4};0 )$

b) Trục đối xứng $x = - {1 \over 4}$ $x = - {1 \over 4}$ ; đỉnh $I( - {1 \over 4}; - {{17} \over 8})$ $I( - {1 \over 4}; - {{17} \over 8})$ giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm $( - {{1 + \sqrt {17} } \over 4};0)$ $( - {{1 + \sqrt {17} } \over 4};0)$ và $({{\sqrt {17} - 1} \over 4};0)$ $({{\sqrt {17} - 1} \over 4};0)$

c) Trục đối xứng x = 2; đỉnh I(2;1); giao với trục tung tại điểm (0;-1) giao với trục hoành tại các điểm $(1 + \sqrt 2 ;0)$ $(1 + \sqrt 2 ;0)$ và $(2 - \sqrt 2 ;0)$ $(2 - \sqrt 2 ;0)$

d) Trục đối xứng x = 5; đỉnh I(5;1); giao với trục tung tại điểm (0;6). Parabol không cắt trục hoành $(\Delta = - {4 \over 5} < 0)$ $(\Delta = - {4 \over 5} < 0)$

Bài 15 trang 40 Sách bài tập (SBT) Toán 10

Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai

a) $y = 2{x^2} + 4x - 6$ $y = 2{x^2} + 4x - 6$

b) $y = - 3{x^2} - 6x + 4$ $y = - 3{x^2} - 6x + 4$

c) $y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2$ $y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2$

d) $y = - 2({x^2} + 1)$ $y = - 2({x^2} + 1)$

Gợi ý làm bài

a) Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;

Vậy $- {b \over {2a}} = - 1;\Delta = {b^2} - 4ac = 64; - {\Delta \over {4a}} = - 8$ $- {b \over {2a}} = - 1;\Delta = {b^2} - 4ac = 64; - {\Delta \over {4a}} = - 8$

Vì a > 0, ta có bảng biến thiên

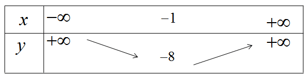
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số nghịch biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$ đồng biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$

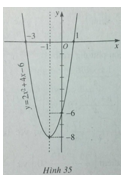
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).

Đồ thị của hàm số $y = 2{x^2} + 4x - 6$ $y = 2{x^2} + 4x - 6$ được vẽ trên hình 35.

Giải bài tập Toán 10 SBT bài 3 chương 2

b) Bảng biến thiên

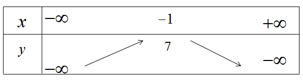
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số đồng biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$ và nghịch biến trên khoảng $( - 1; + \infty )$ $( - 1; + \infty )$

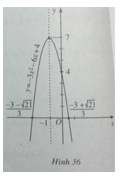
Đỉnh parabol I(-1;7). Đồ thị của hàm số $y = - 3{x^2} - 6x + 4$ $y = - 3{x^2} - 6x + 4$ được vẽ trên hình 36.

Giải bài tập Toán 10 SBT bài 3 chương 2

c) Bảng biến thiên

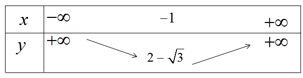
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số nghịch biến trên khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$ và đồng biến trên khoảng $( - 1; + \infty )$ $( - 1; + \infty )$

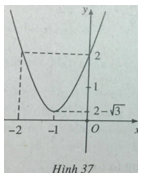
Đỉnh parabol $( - 1;2 - \sqrt 3 )$ $( - 1;2 - \sqrt 3 )$

Đồ thị hàm số được vẽ trên hình 37.

Giải bài tập Toán 10 SBT bài 3 chương 2

d) $y = - 2{x^2} - 2$ $y = - 2{x^2} - 2$

Bảng biến thiên

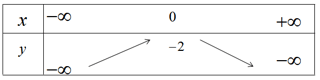
Giải bài tập Toán 10 SBT bài 3 chương 2

Hàm số đồng biến trên khoảng $( - \infty ;0)$ $( - \infty ;0)$ và nghịch biến trên khoảng $(0; + \infty )$ $(0; + \infty )$, hàm số là chẵn.

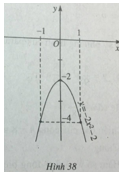
Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4).

Đồ thị hàm số $y = - 2({x^2} + 1)$ $y = - 2({x^2} + 1)$ được vẽ trên hình 38.

Giải bài tập Toán 10 SBT bài 3 chương 2

Bài 16 trang 40 Sách bài tập (SBT) Toán Đại số 10

Xác định hàm số bậc hai y=ax²−4x+c, biết rằng đồ thị của nó

a) Đi qua hai điểm A(1;-2) và B(2;3);

b) Có đỉnh là I(-2 ;-1) ;

c) Có hoành độ đỉnh là -3 và đi qua điểm P(-2 ;1) ;

d) Có trục đối xứng là đường thẳng x = 2 và cắt trục hoành tại điểm M(3 ;0).

Gợi ý làm bài

Các hàm số bậc hai cần xác định đều có b = -4.

a) Ta có

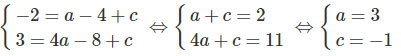
Giải bài tập Toán 10 SBT bài 3 chương 2

Vậy hàm số cần tìm là $y = 3{x^2} - 4x - 1$ $y = 3{x^2} - 4x - 1$

b) $y = - {x^2} - 4x - 5$ $y = - {x^2} - 4x - 5$

c) $y = - {2 \over 3}{x^2} - 4x - {{13} \over 3}$ $y = - {2 \over 3}{x^2} - 4x - {{13} \over 3}$

d) $y = {x^2} - 4x + 3$ $y = {x^2} - 4x + 3$

Bài 17 trang 40 Sách bài tập (SBT) Toán Đại số 10

Viết phương trình của parabol $y = a{x^2} + bx + c$ $y = a{x^2} + bx + c$ ứng với mỗi đồ thị dưới đây

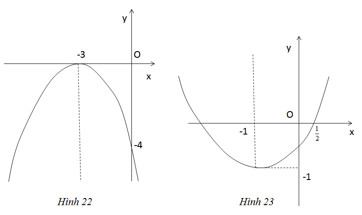
Giải bài tập Toán 10 SBT bài 3 chương 2

Gợi ý làm bài

a) Dựa trên đồ thị (h.22) ta thấy parabol có đỉnh I(-3 ;0) và đi qua điểm (0 ;-4). Như vậy

$c = - 4; - {b \over {2a}} = - 3 \Leftrightarrow b = 6a$ $c = - 4; - {b \over {2a}} = - 3 \Leftrightarrow b = 6a$ Thay c = -4 và b = 6a vào biểu thức

$\Delta = {b^2} - 4ac = 0 = > 36{a^2} + 16a = 0 = > a = - {4 \over 9}$ $\Delta = {b^2} - 4ac = 0 = > 36{a^2} + 16a = 0 = > a = - {4 \over 9}$ vì a ≠ 0 và $b = - {8 \over 3}$ $b = - {8 \over 3}$

Vậy phương trình của parabol là $y = - {4 \over 9}{x^2} - {8 \over 3}x - 4$ $y = - {4 \over 9}{x^2} - {8 \over 3}x - 4$

b) $y = {4 \over 9}{x^2} + {8 \over 9}x - {5 \over 9}$ $y = {4 \over 9}{x^2} + {8 \over 9}x - {5 \over 9}$

Bài 18 trang 40 Sách bài tập (SBT) Toán Đại số 10

Một chiếc ăng – ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4 m. Ở mặt cắt qua trục ta được một parabol dạng y=ax² (h.24). Hãy xác định hệ số a.

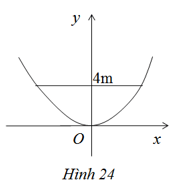
Giải bài tập Toán 10 SBT bài 3 chương 2

Gợi ý làm bài

Ta có thiết diện mặt cắt qua trục của chiếc ăng-ten là:

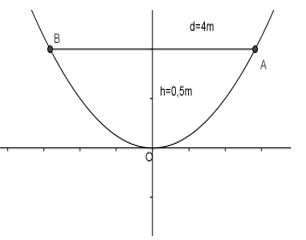
Giải bài tập Toán 10 SBT bài 3 chương 2

Vậy ta có: $A\left( {2;{1 \over 2}} \right)$ $A\left( {2;{1 \over 2}} \right)$ mà $A \in prapol: y = ax_{}^2 \Rightarrow {1 \over 2} = a.2_{}^2 \Leftrightarrow a = {1 \over 8}$ $A \in prapol: y = ax_{}^2 \Rightarrow {1 \over 2} = a.2_{}^2 \Leftrightarrow a = {1 \over 8}$

Bài 19 trang 40 Sách bài tập Toán 10

Một chiếc cổng hình parabol dạng $y = - {1 \over 2}{x^2}$ $y = - {1 \over 2}{x^2}$có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).

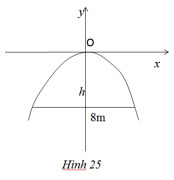
Giải bài tập Toán 10 SBT bài 3 chương 2

Gợi ý làm bài

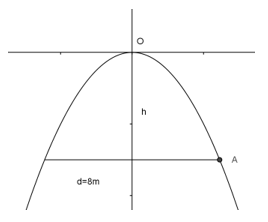
Giải bài tập Toán 10 SBT bài 3 chương 2

Ta có: $A\left( {4; - h} \right)$ $A\left( {4; - h} \right)$ mà $A \in parabol y = - {1 \over 2}x_{}^2 \Rightarrow h = \left| { - {1 \over 2}.4_{}^2} \right| \Rightarrow h = 8$ $A \in parabol y = - {1 \over 2}x_{}^2 \Rightarrow h = \left| { - {1 \over 2}.4_{}^2} \right| \Rightarrow h = 8$

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

603