Giải bài tập Toán 10 SBT bài 2 chương 2

Toán 10 - Hàm số y = ax + b

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT bài 2 chương 2, tài liệu gồm 7 bài tập trang 34, 35 kèm theo đáp án sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán 10 một cách hiệu quả hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT bài 2

Bài 7 trang 34 Sách bài tập (SBT) Toán 10

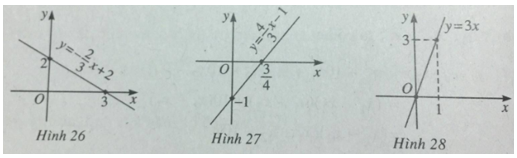
Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng

a) \(y = - {2 \over 3}x + 2\)

b) \(y = {4 \over 3}x - 1\)

c) \(y = 3x\)

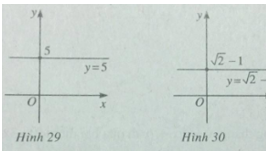
d) y = 5

e) \(y = \sqrt 2 - 1\)

Gợi ý làm bài

a) Đồ thị là hình 26. Hàm số không là hàm số chẵn, không là hàm số lẻ.

b) Đồ thị là hình 27. Hàm số không là hàm số chẵn, không là hàm số lẻ.

c) Đồ thị là hình 28. Hàm số là hàm số lẻ.

d) Đồ thị là hình 29. Hàm số là hàm số chẵn.

e) Đồ thị là hình 30. Hàm số là hàm số chẵn.

Bài 8 trang 34 Sách bài tập (SBT) Toán Đại số 10

Vẽ đồ thị hàm số

\(y = \left\{ \matrix{ 2x - 1,x \ge - 1 \hfill \cr {1 \over 2}x + 1,x < 1 \hfill \cr} \right.\)

Gợi ý làm bài

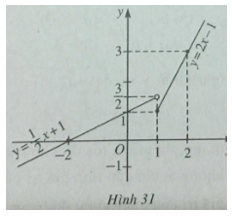
Đồ thị hàm số được vẽ trên hình 31. Điểm (1 ;1) thuộc đồ thị, điểm \((1;{3 \over 2})\) không thuộc đồ thị.

Bài 9 trang 34 Sách bài tập (SBT) Toán Đại số 10

Viết phương trình đường thẳng song song với đường thẳng y = 3x - 2 và đi qua điểm

a) M (2 ;3);

b) N (-1 ;2).

Gợi ý làm bài

Các đường thẳng đều có phương trình dạng y = ax+b. Các đường thẳng song song với nhau đều có cùng một hệ số a. Do đó các phương trình của các đường thẳng song song với đường thẳng y = 3x - 2 đều có hệ số a = 3

a) Phương tình cần tìm có dạng y = 3x + b.

Vì đường thẳng đi qua điểm M(2;3), nên ta có 3=3.2+b⇔b=−3

Vậy phương trình của đường thẳng đó là y = 3x - 3

b) y = 3x + 5

Bài 10 trang 34 Sách bài tập (SBT) Toán Đại số 10

Xác định các hệ số a và b để đồ thị của hàm số y = ax + b đi qua các điểm sau

a) \(A({2 \over 3}; - 2)\)và B(0 ;1);

b) M(−1;−2) và N(99;−2)

c) P(4 ;2) và Q(1 ;1).

Gợi ý làm bài

Để xác định các hệ số a và b ta dựa vào tọa độ các điểm mà đồ thị đi qua, lập hệ phương trình có hai ẩn a và b.

a) Vì đồ thị đi qua \(A({2 \over 3}; - 2)\) nên ta có phương trình \(a.{2 \over 3} + b = - 2\)

Tương tự, dựa vào tọa độ của B(0 ;1) ta có 0 + b =1.

Vậy, ta có hệ phương trình.

\(\left\{ \matrix{ {{2a} \over 3} + b = - 2 \hfill \cr b = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = - {9 \over 2} \hfill \cr b = 1 \hfill \cr} \right.\)

b) \(a = 0;b = - 2\)

c) \(a = {1 \over 3};b = {2 \over 3}\)

Bài 11 trang 34 Sách bài tập (SBT) Toán Đại số 10

Viết phương trình đường thẳng y = ax + b ứng với hình sau

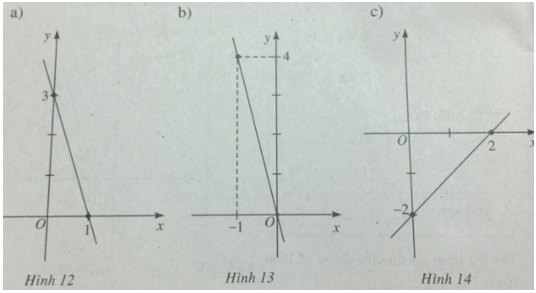
Gợi ý làm bài

a) Ta thấy đường thẳng y = ax + b đi qua hai điểm (0; 3) và (1; 0). Vậy ta có:

\(\left\{ \matrix{ 3 = b \hfill \cr 0 = a + b \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = - 3 \hfill \cr b = 3 \hfill \cr} \right.\)

Đường thẳng có phương trình là y = -3x + 3

b) y = -4x

c) y = x - 2

Bài 12 trang 35 Sách bài tập (SBT) Toán Đại số 10

Cho hàm số \(y = | - x - 3| + |2x + 1| + |x + 1|\). Xét xem điểm nào trong các điểm sau đây thuộc đồ thị của nó.

a) A(-1; 3);

b) B(0; 6);

c) C(5; -2;

d) D(1; 10).

Gợi ý làm bài

Để xét xem một điểm với tọa độ cho trước có thuộc đồ thị của hàm số y = f(x) hay không ta chỉ cần tính giá trị của hàm số tại hoành độ của điểm đã cho. Nếu giá trị của hàm số tại đó bằng tung độ của điểm đang xét thì điểm đó thuộc đồ thị, còn nếu ngược lại thì điểm đang xét không thuộc đồ thị.

a) Với điểm A(-1 ; 3). Ta có

\(| - ( - 1) - 3| + |2.( - 1) + 1| + | - 1 + 1| = 2 + 1 + 0 = 3\), bằng tung độ của điểm A do đó điểm A thuộc đồ thị;

b) Điểm B không thuộc đồ thị;

c) Điểm C không thuộc đồ thị;

d) Điểm D không thuộc đồ thị.

Bài 13 trang 35 Sách bài tập (SBT) Toán Đại số 10

Lập bảng biến thiên và vẽ đồ thị của mỗi hàm số

a) \(y = |2x - 3|\)

b) \(y = | - {3 \over 4}x + 1|\)

c) \(y = x + |x|\)

Gợi ý làm bài

a) Ta có thể viết

\(y = \left\{ \matrix{ 2x - 3,x \ge {3 \over 2} \hfill \cr - 2x + 3,x < {3 \over 2} \hfill \cr} \right.\)

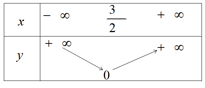
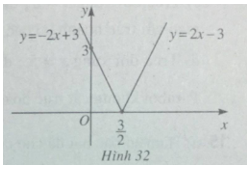
Từ đó có bảng biến thiên và đồ thị của hàm số \($$y = |2x - 3|$$\) (h.32)

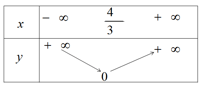
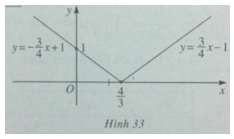
b) Bảng biến thiên và đồ thị của hàm số \(y = | - {3 \over 4}x + 1|\) (h.33)

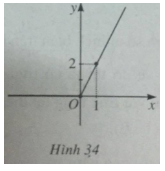
c) Ta có thể viết

\(y = \left\{ \matrix{0,x < 0 \hfill \cr 2x,x \ge 0 \hfill \cr} \right.\)

và đồ thị của hàm số \(y = x + |x|\) được vẽ trên hình 34.

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.