Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 10 SBT ôn tập chương 2

Hàm số bậc nhất và bậc hai

Toán 10 - Hàm số bậc nhất và bậc hai

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT ôn tập chương 2, tài liệu gồm 6 bài tập trang 41, 42 kèm theo lời giải chi tiết sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán lớp 10 một cách đơn giản hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT ôn tập chương 1

Giải bài tập Toán 10 SBT bài 1 chương 2

Giải bài tập Toán 10 SBT bài 2 chương 2

Giải bài tập Toán 10 SBT bài 3 chương 2

Giải bài tập Toán 10 SBT ôn tập chương 2

Bài 20 trang 41 Sách bài tập (SBT) Toán 10

Hai hàm số y = x + 4 và $y = {{{x^2} - 16} \over {x - 4}}$ $y = {{{x^2} - 16} \over {x - 4}}$ có chung một tập xác định hay không?

Gợi ý làm bài

Đáp án: Không.

Vì Hàm số y = x + 4 TXĐ: D = R

Hàm số TXĐ: $y = {{{x^2} - 16} \over {x - 4}}$ $y = {{{x^2} - 16} \over {x - 4}}$ D = R\{4}

Bài 21 trang 41 Sách bài tập (SBT) Toán Đại số 10

Cho hàm số y = f(x) nghịch biến trên khoảng (a;b), khi đó hàm số y =-f(x) có chiều biến thiên như thế nào trên khoảng (a ; b)?

Gợi ý làm bài

Do hàm số y=f(x) nghịch biến trên khoảng (a;b) nên

∀x₁<x₂∈(a;b):f(x₁)>f(x₂)

⇔−f(x₁)<−f(x₂)

Vậy hàm số $y = - f(x)$ đồng biến trên khoảng (a;b).

Bài 22 trang 42 Sách bài tập (SBT) Toán 10

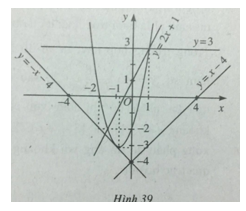
Tìm giao điểm của parabol y=2x²+3x−2 với các đường thẳng

a) y = 2x + 1;

b) y = x – 4;

c) y = -x – 4;

d) y = 3.

Hướng dẫn. Để xác định hoành độ giao điểm của hai đồ thị có phương trình tương ứng là và ta phải giải phương trình f(x)=g(x)

Gợi ý làm bài

a) Xét phương trình:

$2{x^2} + 3x - 2 = 2x + 1 \Leftrightarrow 2{x^2} + x - 3 = 0 \Leftrightarrow \left[ \matrix{ {x_1} = 1 \hfill \cr {x_2} = - {3 \over 2} \hfill \cr} \right.$ $2{x^2} + 3x - 2 = 2x + 1 \Leftrightarrow 2{x^2} + x - 3 = 0 \Leftrightarrow \left[ \matrix{ {x_1} = 1 \hfill \cr {x_2} = - {3 \over 2} \hfill \cr} \right.$

Vậy parabol đã cho và đường thẳng y = 2x + 1 có hai giao điểm là (1;3) và $( - {3 \over 2}; - 2)$ $( - {3 \over 2}; - 2)$

b) Xét phương trình $2{x^2} + 3x - 2 = x - 4$ $2{x^2} + 3x - 2 = x - 4$

⇔2x²+2x+2=0

⇔x²+x+1=0(∗)

Phương trình (*) có biệt thức $\Delta = 1 - 4 = - 3 < 0$ $\Delta = 1 - 4 = - 3 < 0$, do đó phương trình vô nghiệm.

Vậy parabol đã cho và đường thẳng y = x – 4 không có giao điểm.

c) Xét phương trình

$2{x^2} + 3x - 2 = - x - 4 \Leftrightarrow 2{x^2} + 4x + 2 = 0$ $2{x^2} + 3x - 2 = - x - 4 \Leftrightarrow 2{x^2} + 4x + 2 = 0$

${x^2} + 2x + 1 = 0 = > x = - 1$ ${x^2} + 2x + 1 = 0 = > x = - 1$

Vậy parabol đã cho và đường thẳng y = -x – 4 tiếp xúc nhau tại điểm có tọa độ (-1;-3).

Đồ thị được vẽ trên hình 39

Giải bài tập Toán 10 SBT ôn tập chương 2

d) Xét phương trình

$2{x^2} + 3x - 2 = 3 \Leftrightarrow 2{x^2} + 3x - 5 = 0 \Leftrightarrow \left[ \matrix{ {x_1} = 1 \hfill \cr {x_2} = - {5 \over 2} \hfill \cr} \right.$ $2{x^2} + 3x - 2 = 3 \Leftrightarrow 2{x^2} + 3x - 5 = 0 \Leftrightarrow \left[ \matrix{ {x_1} = 1 \hfill \cr {x_2} = - {5 \over 2} \hfill \cr} \right.$

Vậy có hai giao điểm là (1;3) và $( - {5 \over 2};3)$ $( - {5 \over 2};3)$

Bài 23 trang 42 Sách bài tập (SBT) Toán Đại số 10

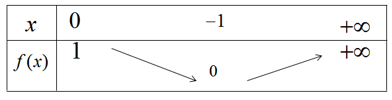
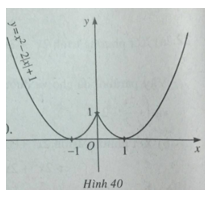
Lập bảng biến thiên và vẽ đồ thị hàm số y=x²−2|x|+1

Gợi ý làm bài

Tập xác định của hàm số là D = R. Ngoài ra f(−x)=(−x)²−2|−x|+1=x²−2|x|+1=f(x)

Hàm số là hàm số chẵn. Đồ thị của nó nhận trục tung làm trục đối xứng. Để xét chiều biến thiên và vẽ đồ thị của nó chỉ cần xét chiều biến thiên và vẽ đồ thị của nó trên nửa khoảng [0;+∞)[0;+∞), rồi lấy đối xứng qua Oy. Với x≥0 có f(x)=x²−2x+1

Bảng biến thiên

Đồ thị của hàm số đã cho được vẽ ở hình 40.

Giải bài tập Toán 10 SBT ôn tập chương 2

Bài 24 trang 42 Sách bài tập (SBT) Toán Đại số 10

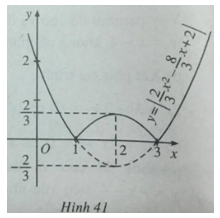
Vẽ đồ thị của hàm số $y = \left| {{2 \over 3}{x^2} - {8 \over 3}x + 2} \right|$ $y = \left| {{2 \over 3}{x^2} - {8 \over 3}x + 2} \right|$

Gợi ý làm bài

Vì $\left| {f(x)} \right| = \left\{ \matrix{f(x),f(x) \ge 0 \hfill \cr - f(x),f(x) < 0 \hfill \cr} \right.$ $\left| {f(x)} \right| = \left\{ \matrix{f(x),f(x) \ge 0 \hfill \cr - f(x),f(x) < 0 \hfill \cr} \right.$

Nên để vẽ đồ thị của hàm số y = |f(x)| ta vẽ đồ thị của hàm số y =f(x), sau đó giữ nguyên phần đồ thị ở phía trên trục hoành và lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.

Trong trường hợp này, ta vẽ đồ thị của hàm số $y = {2 \over 3}{x^2} - {8 \over 3}x + 2$ $y = {2 \over 3}{x^2} - {8 \over 3}x + 2$, sau đó giữ nguyên phần đồ thị ứng với các nửa khoảng $( - \infty ;1]$ $( - \infty ;1]$ và ${\rm{[}}3; + \infty )$ ${\rm{[}}3; + \infty )$. Lấy đối xứng phần đồ thị ứng với khoảng (1;3) qua trục hoành.

Đồ thị của hàm số $y = \left| {{2 \over 3}{x^2} - {8 \over 3}x + 2} \right|$ $y = \left| {{2 \over 3}{x^2} - {8 \over 3}x + 2} \right|$ được vẽ trên hình 41 (đường nét liền)

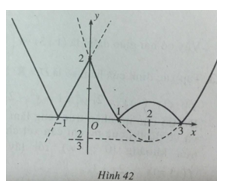
Giải bài tập Toán 10 SBT ôn tập chương 2

Bài 25 trang 42 Sách bài tập (SBT) Toán Đại số 10

Cho hàm số

$y = f(x) = \left\{ \matrix{ {2 \over 3}{x^2} - {8 \over 3}x + 2,x > 0 \hfill \cr 2x + 2,x \le 0 \hfill \cr} \right.$ $y = f(x) = \left\{ \matrix{ {2 \over 3}{x^2} - {8 \over 3}x + 2,x > 0 \hfill \cr 2x + 2,x \le 0 \hfill \cr} \right.$

Vẽ đồ thị của hàm số $y = \left| {f(x)} \right|$ $y = \left| {f(x)} \right|$

Gợi ý làm bài

Với x >0 ta có đồ thị của y = |f(x)| như hình 41 (bỏ phần ứng với $x \le 0$ $x \le 0$)

Với $x \le 0$ $x \le 0$, trước hết vẽ đồ thị hàm số y = 2x + 2. Giữ yên phần đồ thị đoạn [-1;0], bỏ đi phần đồ thị ứng với khoảng $( - \infty ; - 1)$ $( - \infty ; - 1)$, thay vào đó là phần đối xứng với phần bỏ đi qua trục hoành. Đồ thị hàm số y = f|(x)| được vẽ trên hình 42 (đường nét liền).

Giải bài tập Toán 10 SBT ôn tập chương 2