VnDoc.com

Giải bài tập Toán 10 SBT bài 2 chương 6

Giá trị lượng giác của một cung

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Giải bài tập

Loại File: PDF

Phân loại: Tài liệu Tính phí

Toán 10 - Giá trị lượng giác của một cung

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT bài 2 chương 6, tài liệu gồm 9 bài tập trang 189, 190 kèm theo đáp án sẽ là nguồn thông tin hữu ích để giúp các bạn học sinh học tập môn Toán được tốt hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT bài 3 chương 5

Giải bài tập Toán 10 SBT bài 4 chương 5

Giải bài tập Toán 10 SBT ôn tập chương 5

Giải bài tập Toán 10 SBT bài 1 chương 6

Giải bài tập Toán 10 SBT bài 2

Bài 7 trang 189 Sách bài tập (SBT) Toán Đại số 10

Cho $\pi < \alpha < {{3\pi } \over 2}$ $\pi < \alpha < {{3\pi } \over 2}$. Xác định dấu của các giá trị lượng giác sau

a) $\cos (\alpha - {\pi \over 2});$ $\cos (\alpha - {\pi \over 2});$

b) $\sin ({\pi \over 2} + \alpha );$ $\sin ({\pi \over 2} + \alpha );$

c) $\tan ({{3\pi } \over 2} - \alpha );$ $\tan ({{3\pi } \over 2} - \alpha );$

d) $\cot (\alpha + \pi )$ $\cot (\alpha + \pi )$

Gợi ý làm bài

a) Với $\pi < \alpha < {{3\pi } \over 2}$ $\pi < \alpha < {{3\pi } \over 2}$ thì ${\pi \over 2} < \alpha - {\pi \over 2} < \pi$ ${\pi \over 2} < \alpha - {\pi \over 2} < \pi$, do đó $\cos (\alpha - {\pi \over 2}) < 0.$ $\cos (\alpha - {\pi \over 2}) < 0.$

b) ${{3\pi } \over 2} < {\pi \over 2} + \alpha < 2\pi$ ${{3\pi } \over 2} < {\pi \over 2} + \alpha < 2\pi$ nên $\sin ({\pi \over 2} + \alpha ) < 0$ $\sin ({\pi \over 2} + \alpha ) < 0$

c) $0 < {{3\pi } \over 2} - \alpha < {\pi \over 2}$ $0 < {{3\pi } \over 2} - \alpha < {\pi \over 2}$ nên $\tan ({{3\pi } \over 2} - \alpha ) > 0$ $\tan ({{3\pi } \over 2} - \alpha ) > 0$

d) $\pi < \alpha + \pi < {{5\pi } \over 2}$ $\pi < \alpha + \pi < {{5\pi } \over 2}$ nên $\cot (\alpha + \pi ) > 0$ $\cot (\alpha + \pi ) > 0$

Bài 8 trang 189 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng với mọi $\alpha$ $\alpha$, ta luôn có

a) $\sin (\alpha + {\pi \over 2}) = \cos \alpha;$ $\sin (\alpha + {\pi \over 2}) = \cos \alpha;$

b) ${\rm{cos}}(\alpha + {\pi \over 2}) = - \sin \alpha ;$ ${\rm{cos}}(\alpha + {\pi \over 2}) = - \sin \alpha ;$

c) $\tan (\alpha + {\pi \over 2}) = - \cot \alpha;$ $\tan (\alpha + {\pi \over 2}) = - \cot \alpha;$

d) $\cot (\alpha + {\pi \over 2}) = - \tan \alpha.$ $\cot (\alpha + {\pi \over 2}) = - \tan \alpha.$

Gợi ý làm bài

a) $\sin (\alpha + {\pi \over 2}) = \sin ({\pi \over 2} - ( - \alpha )) = c{\rm{os( - }}\alpha {\rm{) = cos}}\alpha$ $\sin (\alpha + {\pi \over 2}) = \sin ({\pi \over 2} - ( - \alpha )) = c{\rm{os( - }}\alpha {\rm{) = cos}}\alpha$

b) ${\rm{cos}}(\alpha + {\pi \over 2}) = c{\rm{os(}}{\pi \over 2} - ( - \alpha ) = \sin ( - \alpha ) = - \sin \alpha$ ${\rm{cos}}(\alpha + {\pi \over 2}) = c{\rm{os(}}{\pi \over 2} - ( - \alpha ) = \sin ( - \alpha ) = - \sin \alpha$

c) $\tan (\alpha + {\pi \over 2}) = {{\sin (\alpha + {\pi \over 2})} \over {\cos (\alpha + {\pi \over 2})}} = {{\cos \alpha } \over { - \sin \alpha }} = - \cot \alpha$ $\tan (\alpha + {\pi \over 2}) = {{\sin (\alpha + {\pi \over 2})} \over {\cos (\alpha + {\pi \over 2})}} = {{\cos \alpha } \over { - \sin \alpha }} = - \cot \alpha$

d) $\cot (\alpha + {\pi \over 2}) = {{\cos (\alpha + {\pi \over 2})} \over {\sin (\alpha + {\pi \over 2})}} = {{ - \sin \alpha } \over {\cos \alpha }} = - \tan \alpha$ $\cot (\alpha + {\pi \over 2}) = {{\cos (\alpha + {\pi \over 2})} \over {\sin (\alpha + {\pi \over 2})}} = {{ - \sin \alpha } \over {\cos \alpha }} = - \tan \alpha$

Bài 9 trang 189 Sách bài tập (SBT) Toán Đại số 10

Tính các giá trị lượng giác của góc $\alpha$ $\alpha$, nếu

a) ${\rm{cos}}\alpha = - {1 \over 4},\pi < \alpha < {{3\pi } \over 2}$ ${\rm{cos}}\alpha = - {1 \over 4},\pi < \alpha < {{3\pi } \over 2}$

b) ${\rm{sin}}\alpha = {2 \over 3},{\pi \over 2} < \alpha < \pi$ ${\rm{sin}}\alpha = {2 \over 3},{\pi \over 2} < \alpha < \pi$

c) ${\rm{tan}}\alpha = {7 \over 3},0 < \alpha < {\pi \over 2}$ ${\rm{tan}}\alpha = {7 \over 3},0 < \alpha < {\pi \over 2}$

d) ${\rm{cot}}\alpha = - {{14} \over 9},{{3\pi } \over 2} < \alpha < 2\pi$ ${\rm{cot}}\alpha = - {{14} \over 9},{{3\pi } \over 2} < \alpha < 2\pi$

Gợi ý làm bài

a) $\pi < \alpha < {{3\pi } \over 2} = > \sin \alpha < 0$ $\pi < \alpha < {{3\pi } \over 2} = > \sin \alpha < 0$

Vậy $\sin \alpha = - \sqrt {1 - {{\cos }^2}\alpha } = - \sqrt {1 - {1 \over {16}}} = - {{\sqrt {15} } \over 4}$ $\sin \alpha = - \sqrt {1 - {{\cos }^2}\alpha } = - \sqrt {1 - {1 \over {16}}} = - {{\sqrt {15} } \over 4}$

$\tan \alpha = {{\sin \alpha } \over {{\rm{cos}}\alpha }} = \sqrt {15} ,\cot \alpha = {1 \over {\sqrt {15} }}$ $\tan \alpha = {{\sin \alpha } \over {{\rm{cos}}\alpha }} = \sqrt {15} ,\cot \alpha = {1 \over {\sqrt {15} }}$

b) ${\pi \over 2} < \alpha < \pi = > c{\rm{os}}\alpha {\rm{ < 0}}$ ${\pi \over 2} < \alpha < \pi = > c{\rm{os}}\alpha {\rm{ < 0}}$

Vậy $\cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - {4 \over 9}} = {{ - \sqrt 5 } \over 3}$ $\cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - {4 \over 9}} = {{ - \sqrt 5 } \over 3}$

$\tan \alpha = {{\sin \alpha } \over {c{\rm{os}}\alpha }}{\rm{ = - }}{2 \over {\sqrt 5 }}{\rm{,cot}}\alpha {\rm{ = - }}{{\sqrt 5 } \over 2}$ $\tan \alpha = {{\sin \alpha } \over {c{\rm{os}}\alpha }}{\rm{ = - }}{2 \over {\sqrt 5 }}{\rm{,cot}}\alpha {\rm{ = - }}{{\sqrt 5 } \over 2}$

c) $0 < \alpha < {\pi \over 2} = \cos \alpha > 0,co{s^2}\alpha = {1 \over {1 + {{\tan }^2}\alpha }}$ $0 < \alpha < {\pi \over 2} = \cos \alpha > 0,co{s^2}\alpha = {1 \over {1 + {{\tan }^2}\alpha }}$

Vậy $\cos \alpha = {1 \over {\sqrt {1 + {{49} \over 9}} }} = {3 \over {\sqrt {58} }}$ $\cos \alpha = {1 \over {\sqrt {1 + {{49} \over 9}} }} = {3 \over {\sqrt {58} }}$

$\sin \alpha = \cos \alpha \tan \alpha = {7 \over {\sqrt {58} }},\cot \alpha = {3 \over 7}$ $\sin \alpha = \cos \alpha \tan \alpha = {7 \over {\sqrt {58} }},\cot \alpha = {3 \over 7}$

d) ${{3\pi } \over 2} < \alpha < 2\pi = > \sin \alpha < 0,{\sin ^2}\alpha = {1 \over {1 + {{\cot }^2}\alpha }}$ ${{3\pi } \over 2} < \alpha < 2\pi = > \sin \alpha < 0,{\sin ^2}\alpha = {1 \over {1 + {{\cot }^2}\alpha }}$

Vậy $\sin \alpha = - {1 \over {\sqrt {1 + {{196} \over {81}}} }} = - {9 \over {\sqrt {277} }}$ $\sin \alpha = - {1 \over {\sqrt {1 + {{196} \over {81}}} }} = - {9 \over {\sqrt {277} }}$

${\rm{cos}}\alpha {\rm{ = sin}}\alpha {\rm{cot}}\alpha {\rm{ = }}{{14} \over {\sqrt {277} }},\tan \alpha = {1 \over {\cot \alpha }} = - {9 \over {14}}$ ${\rm{cos}}\alpha {\rm{ = sin}}\alpha {\rm{cot}}\alpha {\rm{ = }}{{14} \over {\sqrt {277} }},\tan \alpha = {1 \over {\cot \alpha }} = - {9 \over {14}}$

Bài 10 trang 189 Sách bài tập (SBT) Toán Đại số 10

Biết $\sin \alpha = {3 \over 4}$ $\sin \alpha = {3 \over 4}$ và ${\pi \over 2} < \alpha < \pi$ ${\pi \over 2} < \alpha < \pi$. Tính

a) $A = {{2\tan \alpha - 3\cot \alpha } \over {\cos \alpha + tan\alpha }}$ $A = {{2\tan \alpha - 3\cot \alpha } \over {\cos \alpha + tan\alpha }}$

b) $B = {{{\rm{co}}{{\rm{s}}^2}\alpha + {{\cot }^2}\alpha } \over {\tan \alpha - \cot \alpha }}$ $B = {{{\rm{co}}{{\rm{s}}^2}\alpha + {{\cot }^2}\alpha } \over {\tan \alpha - \cot \alpha }}$

Gợi ý làm bài

a) ${\pi \over 2} < \alpha < \pi = > \cos \alpha < 0$ ${\pi \over 2} < \alpha < \pi = > \cos \alpha < 0$

Ta có: $\cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - {9 \over {16}}} = - {{\sqrt 7 } \over 4}$ $\cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - {9 \over {16}}} = - {{\sqrt 7 } \over 4}$

$\tan \alpha = {{\sin \alpha } \over {\cos \alpha }} = - {3 \over {\sqrt 7 }},\cot \alpha = - {{\sqrt 7 } \over 3}$ $\tan \alpha = {{\sin \alpha } \over {\cos \alpha }} = - {3 \over {\sqrt 7 }},\cot \alpha = - {{\sqrt 7 } \over 3}$

Vậy $A = {{ - {6 \over {\sqrt 7 }} + \sqrt 7 } \over { - {{\sqrt 7 } \over 4} - {3 \over {\sqrt 7 }}}} = - {4 \over {19}}$ $A = {{ - {6 \over {\sqrt 7 }} + \sqrt 7 } \over { - {{\sqrt 7 } \over 4} - {3 \over {\sqrt 7 }}}} = - {4 \over {19}}$

b) $B = {{{7 \over {16}} + {7 \over 9}} \over { - {3 \over {\sqrt 7 }} + {{\sqrt 7 } \over {\sqrt 7 }}}} = {{{{7 \times 25} \over {144}}} \over { - {2 \over {3\sqrt 7 }}}} = - {{175\sqrt 7 } \over {96}}$ $B = {{{7 \over {16}} + {7 \over 9}} \over { - {3 \over {\sqrt 7 }} + {{\sqrt 7 } \over {\sqrt 7 }}}} = {{{{7 \times 25} \over {144}}} \over { - {2 \over {3\sqrt 7 }}}} = - {{175\sqrt 7 } \over {96}}$

Bài 11 trang 189 Sách bài tập (SBT) Toán Đại số 10

Cho $\tan \alpha - 3\cot \alpha = 6$ $\tan \alpha - 3\cot \alpha = 6$ và $\pi < \alpha < {{3\pi } \over 2}$ $\pi < \alpha < {{3\pi } \over 2}$. Tính

a) $\sin \alpha + \cos \alpha$ $\sin \alpha + \cos \alpha$

b) ${{2\sin \alpha - \tan \alpha } \over {{\rm{cos}}\alpha {\rm{ + cot}}\alpha }}$ ${{2\sin \alpha - \tan \alpha } \over {{\rm{cos}}\alpha {\rm{ + cot}}\alpha }}$

Gợi ý làm bài

Vì $\pi < \alpha < {{3\pi } \over 2}$ $\pi < \alpha < {{3\pi } \over 2}$

Nên $\cos \alpha < 0,\sin \alpha < 0$ $\cos \alpha < 0,\sin \alpha < 0$ và $\tan \alpha > 0$ $\tan \alpha > 0$

Ta có: $\tan \alpha - 3\cot \alpha = 6 \Leftrightarrow \tan \alpha - {3 \over {\tan \alpha }} - 6 = 0$ $\tan \alpha - 3\cot \alpha = 6 \Leftrightarrow \tan \alpha - {3 \over {\tan \alpha }} - 6 = 0$

$\Leftrightarrow {\tan ^2}\alpha - 6\tan \alpha - 3 = 0$ $\Leftrightarrow {\tan ^2}\alpha - 6\tan \alpha - 3 = 0$

Vì $\tan \alpha > 0$ $\tan \alpha > 0$ nên $\tan \alpha = 3 + 2\sqrt 3$ $\tan \alpha = 3 + 2\sqrt 3$

a) ${\rm{co}}{{\rm{s}}^2}\alpha = {1 \over {1 + {{\tan }^2}\alpha }} = {1 \over {22 + 12\sqrt 3 }}$ ${\rm{co}}{{\rm{s}}^2}\alpha = {1 \over {1 + {{\tan }^2}\alpha }} = {1 \over {22 + 12\sqrt 3 }}$

Suy ra ${\rm{cos}}\alpha {\rm{ = - }}{1 \over {\sqrt {22 + 12\sqrt 3 } }},\sin \alpha = - {{3 + 2\sqrt 3 } \over {\sqrt {22 + 12\sqrt 3 } }}$ ${\rm{cos}}\alpha {\rm{ = - }}{1 \over {\sqrt {22 + 12\sqrt 3 } }},\sin \alpha = - {{3 + 2\sqrt 3 } \over {\sqrt {22 + 12\sqrt 3 } }}$

$\sin \alpha + c{\rm{os}}\alpha {\rm{ = - }}{{4 + 2\sqrt 3 } \over {\sqrt {22 + 12\sqrt 3 } }}$ $\sin \alpha + c{\rm{os}}\alpha {\rm{ = - }}{{4 + 2\sqrt 3 } \over {\sqrt {22 + 12\sqrt 3 } }}$

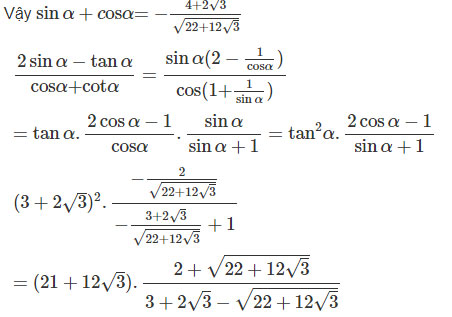
Giải bài tập Toán 10 SBT bài 2 chương 6

Bài 12 trang 189 Sách bài tập (SBT) Toán Đại số 10

Chứng minh các đẳng thức

a) ${{\tan \alpha - \tan \beta } \over {{\rm{cot}}\beta {\rm{ - cot}}\alpha }} = \tan \alpha \tan \beta$ ${{\tan \alpha - \tan \beta } \over {{\rm{cot}}\beta {\rm{ - cot}}\alpha }} = \tan \alpha \tan \beta$

b) $\tan {100^0} + {{\sin {{530}^0}} \over {1 + \sin {{640}^0}}} = {1 \over {\sin {{10}^0}}}$ $\tan {100^0} + {{\sin {{530}^0}} \over {1 + \sin {{640}^0}}} = {1 \over {\sin {{10}^0}}}$

c) $2({\sin ^6}\alpha + c{\rm{o}}{{\rm{s}}^6}\alpha ) + 1 = 3({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha )$ $2({\sin ^6}\alpha + c{\rm{o}}{{\rm{s}}^6}\alpha ) + 1 = 3({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha )$

Gợi ý làm bài

a)

Giải bài tập Toán 10 SBT bài 2 chương 6

Bài 13 trang 190 Sách bài tập (SBT) Toán Đại số 10

Cho $\tan \alpha + \cos \alpha = m$ $\tan \alpha + \cos \alpha = m$, hãy tính theo m

a) ${\tan ^2}\alpha + {\cot ^2}\alpha$ ${\tan ^2}\alpha + {\cot ^2}\alpha$

b) ${\tan ^3}\alpha + {\cot ^3}\alpha$ ${\tan ^3}\alpha + {\cot ^3}\alpha$

Gợi ý làm bài

a)

tan²α+cot²α

=(tanα+cotα)²−2tanαcotα=m²−2

b)

tan³α+cot³α

=(tanα+cotα)(tan²α−tanαcotα+cot²α)

=m(m²−3)

Bài 14 trang 190 Sách bài tập (SBT) Toán Đại số 10

Không dùng bảng số và máy tính, rút gọn các biểu thức

a) $A = \tan {18^0}\tan {288^0} + \sin {32^0}\sin {148^0} - \sin {302^0}\sin {122^0}$ $A = \tan {18^0}\tan {288^0} + \sin {32^0}\sin {148^0} - \sin {302^0}\sin {122^0}$

b) $B = {{1 + {{\sin }^4}\alpha - c{\rm{o}}{{\rm{s}}^4}\alpha } \over {1 - {{\sin }^6}\alpha - c{\rm{o}}{{\rm{s}}^6}\alpha }}$ $B = {{1 + {{\sin }^4}\alpha - c{\rm{o}}{{\rm{s}}^4}\alpha } \over {1 - {{\sin }^6}\alpha - c{\rm{o}}{{\rm{s}}^6}\alpha }}$

Gợi ý làm bài

a)

$A = \tan ({90^0} - {72^0})\tan ({360^0} - {72^0}) + \sin {32^0}\sin ({180^0} - {32^0}) - \sin ({360^0} - {58^0})\sin ({180^0} - {58^0})$ $A = \tan ({90^0} - {72^0})\tan ({360^0} - {72^0}) + \sin {32^0}\sin ({180^0} - {32^0}) - \sin ({360^0} - {58^0})\sin ({180^0} - {58^0})$

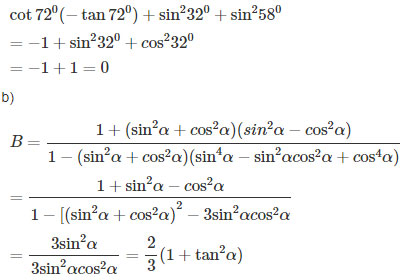
Giải bài tập Toán 10 SBT bài 2 chương 6

Bài 15 trang 190 Sách bài tập (SBT) Toán 10

Chứng minh rằng với mọi $\alpha$ $\alpha$ làm cho biểu thức ${{\sin \alpha + \tan \alpha } \over {{\rm{cos}}\alpha {\rm{ + cot}}\alpha }}$ ${{\sin \alpha + \tan \alpha } \over {{\rm{cos}}\alpha {\rm{ + cot}}\alpha }}$ có nghĩa, biểu thức đó không thể là một số âm.

Gợi ý làm bài

Ta có:

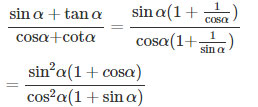
Giải bài tập Toán 10 SBT bài 2 chương 6

Vì $1 + c{\rm{os}}\alpha \ge {\rm{0}}$ $1 + c{\rm{os}}\alpha \ge {\rm{0}}$ và $1 + \sin \alpha \ge {\rm{0}}$ $1 + \sin \alpha \ge {\rm{0}}$ cho nên biểu thức đã cho không thể có giá trị là một số âm.

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Tải về

Chọn file muốn tải về:

Giải bài tập Toán 10 SBT bài 2 chương 6

350,3 KB

Giải bài tập Toán 10 SBT bài 2 chương 6 .DOC
474 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Phan Thị Hoàn

1

172

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!