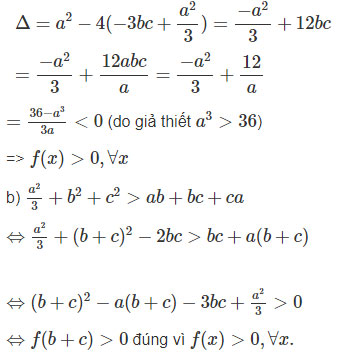Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 10 SBT ôn tập chương 4

Bất đẳng thức. Bất phương trình

Toán 10 - Bất đẳng thức. Bất phương trình

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT ôn tập chương 4, tài liệu kèm theo đáp án sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán lớp 10 một cách chính xác nhất. Mời các bạn học sinh và thầy cô cùng tham khảo.

Giải bài tập Toán 10 SBT bài 2 chương 4

Giải bài tập Toán 10 SBT bài 3 chương 4

Giải bài tập Toán 10 SBT bài 4 chương 4

Giải bài tập Toán 10 SBT bài 5 chương 4

Giải bài tập Toán 10 SBT

Bài 59 trang 124 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng:

${({x^2} - {y^2})^2} \ge 4xy{(x - y)^2},\forall x,y.$ ${({x^2} - {y^2})^2} \ge 4xy{(x - y)^2},\forall x,y.$

Gợi ý làm bài

${({x^2} - {y^2})^2} - 4xy{(x - y)^2} = {(x - y)^2}{\rm{[(x + y}}{{\rm{)}}^2}{\rm{ - 4xy]}}$ ${({x^2} - {y^2})^2} - 4xy{(x - y)^2} = {(x - y)^2}{\rm{[(x + y}}{{\rm{)}}^2}{\rm{ - 4xy]}}$

$= {(x - y)^2}{(x - y)^2} \ge 0 = > {({x^2} - {y^2})^2} \ge 4xy{(x - y)^2},\forall x,y$ $= {(x - y)^2}{(x - y)^2} \ge 0 = > {({x^2} - {y^2})^2} \ge 4xy{(x - y)^2},\forall x,y$

Bài 60 trang 124 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng:

${x^2} + 2{y^2} + 2xy + y + 1 > 0,\forall x,y.$ ${x^2} + 2{y^2} + 2xy + y + 1 > 0,\forall x,y.$

Gợi ý làm bài

${x^2} + 2{y^2} + 2xy + y + 1 = {(x + y)^2} + {(y + {1 \over 2})^2} + {3 \over 4}\forall x,y$ ${x^2} + 2{y^2} + 2xy + y + 1 = {(x + y)^2} + {(y + {1 \over 2})^2} + {3 \over 4}\forall x,y$

Bài 61 trang 124 Sách bài tập (SBT) Toán Đai số 10

Chứng minh rằng:

$(a + 1)(b + 1)(a + c)(b + c) \ge 16abc$ $(a + 1)(b + 1)(a + c)(b + c) \ge 16abc$, với a, b, c là những số dương tùy ý.

Gợi ý làm bài

$(a + 1)(b + 1)(a + c)(b + c) \ge 2\sqrt a .2\sqrt b .2\sqrt {ac} .2\sqrt {bc}$ $(a + 1)(b + 1)(a + c)(b + c) \ge 2\sqrt a .2\sqrt b .2\sqrt {ac} .2\sqrt {bc}$

$2\sqrt a .2\sqrt b .2\sqrt {ac} .2\sqrt {bc} = 16abc.$ $2\sqrt a .2\sqrt b .2\sqrt {ac} .2\sqrt {bc} = 16abc.$

$=> (a + 1)(b + 1)(a + c)(b + c) \ge 16abc$ $=> (a + 1)(b + 1)(a + c)(b + c) \ge 16abc$

Bài 62 trang 124 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng:

$a + b + b \le {1 \over 2}({a^2}b + {b^2}c + {c^2}a + {1 \over a} + {1 \over b} + {1 \over c})$ $a + b + b \le {1 \over 2}({a^2}b + {b^2}c + {c^2}a + {1 \over a} + {1 \over b} + {1 \over c})$

Với a, b, c là những số dương tùy ý.

Gợi ý làm bài

Theo bài 7 ta có:

${a^2}b + {1 \over b} \ge 2a$ ${a^2}b + {1 \over b} \ge 2a$, do đó

$a \le {1 \over 2}({a^2}b + {1 \over b})$ $a \le {1 \over 2}({a^2}b + {1 \over b})$

Tương tự: $b \le {1 \over 2}({b^2}c + {1 \over c})$ $b \le {1 \over 2}({b^2}c + {1 \over c})$

$c \le {1 \over 2}({c^2}a + {1 \over a})$ $c \le {1 \over 2}({c^2}a + {1 \over a})$

Bài 63 trang 124 Sách bài tập (SBT) Toán Đại số 10

Cho a, b, c là ba số thực thỏa mãn điều kiện ${a^3} > 36$ ${a^3} > 36$ và abc = 1

Xét tam thức bậc hai $f(x) = {x^2} - {\rm{a}}x - 3ac + {{{a^2}} \over 3}$ $f(x) = {x^2} - {\rm{a}}x - 3ac + {{{a^2}} \over 3}$

a) Chứng minh rằng $f(x) > 0,\forall x;$ $f(x) > 0,\forall x;$

b) Từ câu a) suy ra ${{{a^2}} \over 3} + {b^2} + {c^2} > ab + bc + ca$ ${{{a^2}} \over 3} + {b^2} + {c^2} > ab + bc + ca$

Gợi ý làm bài

a) f(x) có

Bài 64 trang 124 Sách bài tập (SBT) Toán Đại số 10

Giải và biện luận bất phương trình sau theo tham số m.

$(m - 1).\sqrt x \le 0$ $(m - 1).\sqrt x \le 0$

Gợi ý làm bài

Điều kiện của bất phương trình là $x \ge 0$ $x \ge 0$

Nếu $m \le 1$ $m \le 1$ $m - 1 \le 0$ $m - 1 \le 0$, bất phương trình đã cho nghiệm đúng với mọi $x \ge 0$ $x \ge 0$

Nếu m > 1 thì m – 1 > 0, bất phương trình đã cho tương đương với

$\sqrt x \le 0 \Leftrightarrow x = 0$ $\sqrt x \le 0 \Leftrightarrow x = 0$

Trả lời: Nếu m≤1 thì tập nghiệm của bất phương trình là [0;+∞)

Nếu m > 1 thì tập nghiệm của bất phương trình là {0}

Bài 65 trang 125 Sách bài tập (SBT) Toán Đại số 10

Tìm a và b để bất phương trình

$(x - 2a + b - 1)(x + a - 2b + 1) \le 0$ $(x - 2a + b - 1)(x + a - 2b + 1) \le 0$

Có tập nghiệm là đoạn [0;2].

Gợi ý làm bài

Tập nghiệm của bất phương trình đã cho là đoạn ${\rm{[}}2a - b + 1; - a + 2b - 1]$ ${\rm{[}}2a - b + 1; - a + 2b - 1]$ (nếu $2a - b + 1 \le - a + 2b - 1$ $2a - b + 1 \le - a + 2b - 1$) hoặc là đoạn ${\rm{[}} - a + 2b - 1;2a - b + 1]$ ${\rm{[}} - a + 2b - 1;2a - b + 1]$ (nếu $- a + 2b - 1 \le 2a - b - 1$ $- a + 2b - 1 \le 2a - b - 1$)

Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:

$(1)\,\left\{ \matrix{2a - b + 1 = 2 \hfill \cr - a + 2b - 1 = 0 \hfill \cr} \right.$ $(1)\,\left\{ \matrix{2a - b + 1 = 2 \hfill \cr - a + 2b - 1 = 0 \hfill \cr} \right.$

hoặc

$(2)\,\left\{ \matrix{2a - b + 1 = 0 \hfill \cr - a + 2b - 1 = 2. \hfill \cr} \right.$ $(2)\,\left\{ \matrix{2a - b + 1 = 0 \hfill \cr - a + 2b - 1 = 2. \hfill \cr} \right.$

Giải (1) ta được a = b = 1. Giải hệ (2) ta được $a = {1 \over 3},b = {5 \over 3}$ $a = {1 \over 3},b = {5 \over 3}$

Đáp số: a = b = 1 hoặc $a = {1 \over 3},b = {5 \over 3}$ $a = {1 \over 3},b = {5 \over 3}$

Bài 66 trang 125 Sách bài tập (SBT) Toán Đại số 10

Tìm a và b (b > -1) để hai bất phương trình sau tương đương

$(x - a + b)(x + 2a - b - 1) \le 0 (1)$ $(x - a + b)(x + 2a - b - 1) \le 0 (1)$

Và $\left| {x + a - 2} \right| \le b + 1.$ $\left| {x + a - 2} \right| \le b + 1.$ (2)

Gợi ý làm bài

(1) $\Leftrightarrow x \in {\rm{[}}\alpha ;\beta {\rm{]}}$ $\Leftrightarrow x \in {\rm{[}}\alpha ;\beta {\rm{]}}$, trong đó

$\left\{ \matrix{\alpha = a - b \hfill \cr \beta = - 2a + b + 1 \hfill \cr} \right.$ $\left\{ \matrix{\alpha = a - b \hfill \cr \beta = - 2a + b + 1 \hfill \cr} \right.$

hoặc

$\left\{ \matrix{\alpha = - 2a + b + 1 \hfill \cr \beta = a - b. \hfill \cr} \right.$ $\left\{ \matrix{\alpha = - 2a + b + 1 \hfill \cr \beta = a - b. \hfill \cr} \right.$

(2) $\Leftrightarrow - (b + 1) \le x + a - 2 \le b + 1$ $\Leftrightarrow - (b + 1) \le x + a - 2 \le b + 1$

$\Leftrightarrow - b - a + 1 \le x \le - a + b + 3$ $\Leftrightarrow - b - a + 1 \le x \le - a + b + 3$

$\Leftrightarrow x \in {\rm{[}} - b - a + 1; - a + b + 3]$ $\Leftrightarrow x \in {\rm{[}} - b - a + 1; - a + b + 3]$

(1) và (2) tương đương khi và chỉ khi ${\rm{[}}\alpha ;\beta {\rm{]}} = {\rm{[}} - b - a + 1; - a + b + 3]$ ${\rm{[}}\alpha ;\beta {\rm{]}} = {\rm{[}} - b - a + 1; - a + b + 3]$, tức là:

$\left\{ \matrix{\alpha = - b - a + 1 \hfill \cr \beta = - a + b + 3 \hfill \cr} \right.$ $\left\{ \matrix{\alpha = - b - a + 1 \hfill \cr \beta = - a + b + 3 \hfill \cr} \right.$

$\Leftrightarrow (3)\left\{ \matrix{a - b = - b - a + 1 \hfill \cr - 2a + b + 1 = - a + b + 3 \hfill \cr} \right.$ $\Leftrightarrow (3)\left\{ \matrix{a - b = - b - a + 1 \hfill \cr - 2a + b + 1 = - a + b + 3 \hfill \cr} \right.$

hoặc

$\left\{ \matrix{- 2a + b + 1 = - b - a + 1 \hfill \cr a - b = - a + b + 3 \hfill \cr} \right.$ $\left\{ \matrix{- 2a + b + 1 = - b - a + 1 \hfill \cr a - b = - a + b + 3 \hfill \cr} \right.$

Hệ phương trình (3) vô nghiệm. Hệ phương trình (4) có nghiệm duy nhất $a = 3,b = {3 \over 2}$ $a = 3,b = {3 \over 2}$

Đáp số: $a = 3,b = {3 \over 2}$ $a = 3,b = {3 \over 2}$

Bài 67 trang 125 Sách bài tập (SBT) Toán Đại số 10

a) Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau

$y = f(x) = \left| {x + 3} \right| - 1;$ $y = f(x) = \left| {x + 3} \right| - 1;$

$y = g(x) = \left| {2x - m} \right|$ $y = g(x) = \left| {2x - m} \right|$; trong đó m là tham số

Xác định hoành độ các giao điểm của mỗi đồ thị với trục hoành.

b) Tìm các giá trị của tham số m để bất phương trình sau nghiệm đúng với mọi giá trị của x

$\left| {2x - m} \right| > \left| {x + 3} \right| - 1$ $\left| {2x - m} \right| > \left| {x + 3} \right| - 1$

Gợi ý làm bài

a) Đồ thị hàm số y = f(x) là đường gấp khúc u’Eu, cắt Ox tại A(-4; 0) và B(-2;0).

Đồ thị hàm số y = g(x) là đường gấp khúc v’Cv, cắt Ox tại $C({m \over 2};0)$ $C({m \over 2};0)$

Khi m thay đổi, điểm C chạy trên Ox; tia Cv luông song song với đường thẳng y = 2x; tia Cv’ luôn song song với đường thẳng y = -2x.

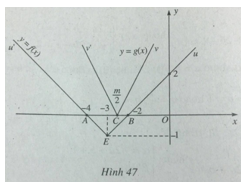
Giải bài tập Toán 10 SBT ôn tập chương 4

b) Bất phương trình đã cho đúng với mọi x khi và chỉ khi đồ thị của hàm số y = g(x) nằm hoàn toàn phía trên đồ thị của hàm số y = f(x) hay C nằm giữa A và B nghĩa là $- 4 < {m \over 2} < - 2 \Leftrightarrow - 8 < m < - 4$ $- 4 < {m \over 2} < - 2 \Leftrightarrow - 8 < m < - 4$

Đáp số: $- 8 < m < - 4$

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

128