Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 10 SBT ôn tập chương 6

Cung và góc lượng giác. Công thức lượng giác

Tải về

Toán 10 - Cung và góc lượng giác. Công thức lượng giác

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT ôn tập chương 6, tài liệu kèm theo đáp án sẽ là nguồn thông tin hữu ích để giúp các bạn học sinh học tập môn Toán 10 một cách hiệu quả hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT ôn tập chương 5

Giải bài tập Toán 10 SBT bài 1 chương 6

Giải bài tập Toán 10 SBT bài 2 chương 6

Giải bài tập Toán 10 SBT bài 3 chương 6

Giải bài tập Toán 10 SBT

Bài 23 trang 195 Sách bài tập (SBT) Toán Đại số 10

Trong các đẳng thức sau, đẳng thức nào đúng, đẳng thức nào sai?

a) $\sin (x + {\pi \over 2}) = \cos x$ $\sin (x + {\pi \over 2}) = \cos x$

b) $cos(x + {\pi \over 2}) = sinx$ $cos(x + {\pi \over 2}) = sinx$

c) $\sin (x - \pi ) = sinx$ $\sin (x - \pi ) = sinx$

d) $cos(x - \pi ) = \cos x$ $cos(x - \pi ) = \cos x$

Gợi ý làm bài

Đáp số:

a) Đúng;

b) Sai;

c) Sai;

d) Sai.

Bài 24 trang 195 Sách bài tập (SBT) Toán Đại số 10

Tồn tại hay không góc α sao cho

a) sinα=−1

b) cosα=0

c) sinα=−0,9

d) cosα=−1,2

e) sinα=1,3

g) sinα=−2?

Gợi ý làm bài

Đáp số:

a) Có;

b) Có;

c) Có;

d) Không, vì -1,2 <-1.

e) Không, vì 1,3 > 1;

Bài 25 trang 195 Sách bài tập (SBT) Toán Đại số 10

Không dùng bảng số và máy tính, hãy xác định dấu của $\sin \alpha$ $\sin \alpha$ và $cos\alpha$ $cos\alpha$ với

a) $\alpha = {135^0}$ $\alpha = {135^0}$

b) $\alpha = {210^0}$ $\alpha = {210^0}$

c) $\alpha = {334^0}$ $\alpha = {334^0}$

d) $\alpha = {1280^0}$ $\alpha = {1280^0}$

e) $\alpha = - {235^0}$ $\alpha = - {235^0}$

g) $\alpha = - {1876^0}$ $\alpha = - {1876^0}$

Gợi ý làm bài

a) $\sin {135^0} > 0,cos{135^0} < 0$ $\sin {135^0} > 0,cos{135^0} < 0$

b) $\sin {210^0} < 0,cos{210^0} < 0$ $\sin {210^0} < 0,cos{210^0} < 0$

c) $\sin {334^0} < 0,cos{334^0} > 0$ $\sin {334^0} < 0,cos{334^0} > 0$

d) sin1280⁰=sin(3.360⁰+120⁰)=sin200⁰<0,

cos1280⁰=cos200⁰<0

e) sin(−235⁰)=sin(−180⁰0−55⁰)=−sin(−55⁰)

=sin55⁰>0,cos(−235⁰)<0

g) sin(−1876⁰)=sin(−1800⁰−76⁰)=sin(−760)=−sin76⁰<0,

cos(−1876⁰)=cos(−76)⁰=cos76⁰>0

Bài 26 trang 195 Sách bài tập (SBT) Toán Đại số 10

Hãy viết theo thứ tự tăng dần các giá trị sau (không dùng bảng số và máy tính)

a) $\sin {40^0},\sin {90^0},\sin {220^0},\sin {10^0}$ $\sin {40^0},\sin {90^0},\sin {220^0},\sin {10^0}$

b) ${\rm{cos}}{15^0},{\rm{cos}}{0^0},{\rm{cos}}{90^0},{\rm{cos}}{138^0}$ ${\rm{cos}}{15^0},{\rm{cos}}{0^0},{\rm{cos}}{90^0},{\rm{cos}}{138^0}$

Gợi ý làm bài

a) $\sin {220^0} < \sin {10^0} < \sin {40^0} < \sin {90^0}$ $\sin {220^0} < \sin {10^0} < \sin {40^0} < \sin {90^0}$

Bài 27 trang 195 Sách bài tập (SBT) Toán Đại số 10

Hãy xác định dấu của các tích (không dùng bảng số và máy tính)

a) $\sin {110^0}cos{130^0}tan{30^0}\cot {320^0}$ $\sin {110^0}cos{130^0}tan{30^0}\cot {320^0}$

b) $\sin ( - {50^0})\tan {170^0}{\rm{cos}}( - {91^0})\sin {530^0}$ $\sin ( - {50^0})\tan {170^0}{\rm{cos}}( - {91^0})\sin {530^0}$

Gợi ý làm bài

a) Ta có: $\sin {110^0} > 0;cos{130^0} < 0;tan{30^0} > 0;\cot {320^0} < 0$ $\sin {110^0} > 0;cos{130^0} < 0;tan{30^0} > 0;\cot {320^0} < 0$, do đó tích của chúng dương.

b) $\sin ( - {50^0}) < 0;\tan {170^0}{\rm{ < 0;cos}}( - {91^0}) < 0;\sin {530^0} > 0$ $\sin ( - {50^0}) < 0;\tan {170^0}{\rm{ < 0;cos}}( - {91^0}) < 0;\sin {530^0} > 0$, do đó tích của chúng âm

Bài 28 trang 195 Sách bài tập (SBT) Toán Đại số 10

Cho tam giác ABC. Hỏi tổng $\sin A + \sin B + \sin C$ $\sin A + \sin B + \sin C$ âm hay dương?

Gợi ý làm bài

Vì các góc $\widehat A,\widehat B,\widehat C$ $\widehat A,\widehat B,\widehat C$là góc trong tam giác ABC nên sinA > 0, sinB >0, sinC >0.

Do đó sinA + sinB + sinC > 0.

Bài 29 trang 195 Sách bài tập (SBT) Toán Đại số 10

Tính các giá trị lượng giác của cung $\alpha$ $\alpha$ biết

a) $\sin \alpha = 0,6$ $\sin \alpha = 0,6$ khi $0 < \alpha < {\pi \over 2}$ $0 < \alpha < {\pi \over 2}$

b) ${\rm{cos}}\alpha = - 0,7$ ${\rm{cos}}\alpha = - 0,7$ khi ${\pi \over 2} < \alpha < \pi$ ${\pi \over 2} < \alpha < \pi$

c) $\tan \alpha = 2$ $\tan \alpha = 2$ khi $\pi < \alpha < {{3\pi } \over 2}$ $\pi < \alpha < {{3\pi } \over 2}$

d) $\cot \alpha = - 3$ $\cot \alpha = - 3$ khi ${{3\pi } \over 2} < \alpha < 2\pi$ ${{3\pi } \over 2} < \alpha < 2\pi$

Gợi ý làm bài

a) $0 < \alpha < {\pi \over 2} = > \cos \alpha > 0$ $0 < \alpha < {\pi \over 2} = > \cos \alpha > 0$, do đó

$\cos \alpha = \sqrt {1 - si{n^2}\alpha } = \sqrt {1 - 0,36} = \sqrt {0,64} = 0,8$ $\cos \alpha = \sqrt {1 - si{n^2}\alpha } = \sqrt {1 - 0,36} = \sqrt {0,64} = 0,8$

$=> \tan \alpha = {3 \over 4},\cot \alpha = {4 \over 3}$ $=> \tan \alpha = {3 \over 4},\cot \alpha = {4 \over 3}$

b) ${\pi \over 2} < \alpha < \pi = > \sin \alpha > 0$ ${\pi \over 2} < \alpha < \pi = > \sin \alpha > 0$, do đó

$\sin \alpha = \sqrt {1 - {{\cos }^2}\alpha } = \sqrt {1 - 0,49} = \sqrt {0,51} \approx 0,71$ $\sin \alpha = \sqrt {1 - {{\cos }^2}\alpha } = \sqrt {1 - 0,49} = \sqrt {0,51} \approx 0,71$

Suy ra: $\tan \alpha = - {{0,7} \over {0,71}} \approx - 0,98,\cot \alpha \approx - 1,01$ $\tan \alpha = - {{0,7} \over {0,71}} \approx - 0,98,\cot \alpha \approx - 1,01$

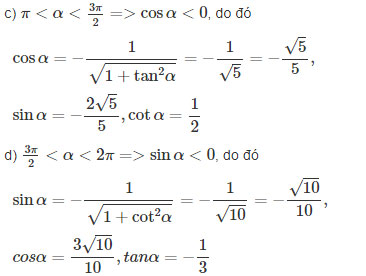
Giải bài tập Toán 10 SBT ôn tập chương 6

Bài 30 trang 196 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng

a) $\sin ({270^0} - \alpha ) = - c{\rm{os}}\alpha$ $\sin ({270^0} - \alpha ) = - c{\rm{os}}\alpha$

b) ${\rm{cos}}({270^0} - \alpha ) = - \sin \alpha$ ${\rm{cos}}({270^0} - \alpha ) = - \sin \alpha$

c) $\sin ({270^0} + \alpha ) = - c{\rm{os}}\alpha$ $\sin ({270^0} + \alpha ) = - c{\rm{os}}\alpha$

d) ${\rm{cos}}({270^0} + \alpha ) = \sin \alpha$ ${\rm{cos}}({270^0} + \alpha ) = \sin \alpha$

Gợi ý làm bài

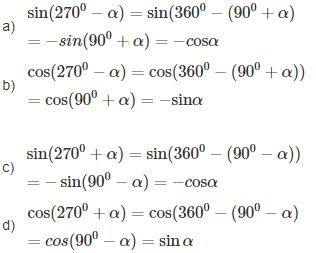
Giải bài tập Toán 10 SBT ôn tập chương 6

Bài 31 trang 196 Sách bài tập (SBT) Toán Đại số 10

Rút gọn các biểu thức (không dùng bảng số và máy tính)

a) ${\sin ^2}({180^0} - \alpha ) + ta{n^2}({180^0} - \alpha ){\tan ^2}({270^0} - \alpha ) + \sin ({90^0} + \alpha )cos(\alpha - {360^0})$ ${\sin ^2}({180^0} - \alpha ) + ta{n^2}({180^0} - \alpha ){\tan ^2}({270^0} - \alpha ) + \sin ({90^0} + \alpha )cos(\alpha - {360^0})$

b) ${{\cos (\alpha - {{90}^0})} \over {\sin ({{180}^0} - \alpha )}} + {{\tan (\alpha - {{180}^0})c{\rm{os(18}}{{\rm{0}}^0} + \alpha )\sin ({{270}^0} + \alpha )} \over {\tan ({{270}^0} + \alpha )}}$ ${{\cos (\alpha - {{90}^0})} \over {\sin ({{180}^0} - \alpha )}} + {{\tan (\alpha - {{180}^0})c{\rm{os(18}}{{\rm{0}}^0} + \alpha )\sin ({{270}^0} + \alpha )} \over {\tan ({{270}^0} + \alpha )}}$

c) ${{\cos ( - {{288}^0})cot{{72}^0}} \over {tan( - {{162}^0})\sin {{108}^0}}} + \tan {18^0}$ ${{\cos ( - {{288}^0})cot{{72}^0}} \over {tan( - {{162}^0})\sin {{108}^0}}} + \tan {18^0}$

d) ${{\sin {{20}^0}\sin {\rm{3}}{{\rm{0}}^0}\sin {{40}^0}\sin {{50}^0}\sin {{60}^0}\sin {{70}^0}} \over {cos{{10}^0}{\rm{cos5}}{{\rm{0}}^0}}}$ ${{\sin {{20}^0}\sin {\rm{3}}{{\rm{0}}^0}\sin {{40}^0}\sin {{50}^0}\sin {{60}^0}\sin {{70}^0}} \over {cos{{10}^0}{\rm{cos5}}{{\rm{0}}^0}}}$

Gợi ý làm bài

$= {\sin ^2}\alpha + {\tan ^2}\alpha {\cot ^2}\alpha + {\cos ^2}\alpha = 2$ $= {\sin ^2}\alpha + {\tan ^2}\alpha {\cot ^2}\alpha + {\cos ^2}\alpha = 2$

$= {{\sin \alpha } \over {\cos \alpha }} + {{\tan \alpha ( - \cos \alpha )( - \cos \alpha )} \over { - \cot \alpha }} = 1 - {\sin ^2}\alpha = {\cos ^2}\alpha$ $= {{\sin \alpha } \over {\cos \alpha }} + {{\tan \alpha ( - \cos \alpha )( - \cos \alpha )} \over { - \cot \alpha }} = 1 - {\sin ^2}\alpha = {\cos ^2}\alpha$

c) ${{\cos ( - {{288}^0})cot{{72}^0}} \over {tan( - {{162}^0})\sin {{108}^0}}} + \tan {18^0}$ ${{\cos ( - {{288}^0})cot{{72}^0}} \over {tan( - {{162}^0})\sin {{108}^0}}} + \tan {18^0}$

$= {{\cos ({{72}^0} - {{360}^0})\cot {{72}^0}} \over {\tan ({{18}^0} - {{180}^0})\sin ({{180}^0} - {{72}^0})}} - \tan {18^0}$ $= {{\cos ({{72}^0} - {{360}^0})\cot {{72}^0}} \over {\tan ({{18}^0} - {{180}^0})\sin ({{180}^0} - {{72}^0})}} - \tan {18^0}$

$= {{{\rm{cos7}}{{\rm{2}}^0}\cot {{72}^0}} \over {\tan {{18}^0}\sin {{72}^0}}} - \tan {18^0}$ $= {{{\rm{cos7}}{{\rm{2}}^0}\cot {{72}^0}} \over {\tan {{18}^0}\sin {{72}^0}}} - \tan {18^0}$

$= {{{{\cot }^2}{{72}^0}} \over {\tan {{18}^0}}} - \tan {18^0} = {{{{\tan }^2}{{18}^0}} \over {\tan {{18}^0}}} - \tan {18^0} = 0$ $= {{{{\cot }^2}{{72}^0}} \over {\tan {{18}^0}}} - \tan {18^0} = {{{{\tan }^2}{{18}^0}} \over {\tan {{18}^0}}} - \tan {18^0} = 0$

d) Ta có: $\sin {70^0} = \cos {20^0},\sin {50^0} = cos4{{\rm{0}}^0};\sin {40^0} = cos{50^0}$ $\sin {70^0} = \cos {20^0},\sin {50^0} = cos4{{\rm{0}}^0};\sin {40^0} = cos{50^0}$. Vì vậy

${{\sin {{20}^0}\sin {\rm{3}}{{\rm{0}}^0}\sin {{40}^0}\sin {{50}^0}\sin {{60}^0}\sin {{70}^0}} \over {cos{{10}^0}{\rm{cos5}}{{\rm{0}}^0}}}$ ${{\sin {{20}^0}\sin {\rm{3}}{{\rm{0}}^0}\sin {{40}^0}\sin {{50}^0}\sin {{60}^0}\sin {{70}^0}} \over {cos{{10}^0}{\rm{cos5}}{{\rm{0}}^0}}}$

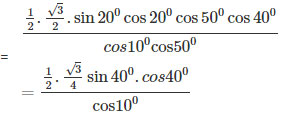
Giải bài tập Toán 10 SBT ôn tập chương 6

$= {{{{\sqrt 3 } \over {16}}\sin {{80}^0}} \over {cos{{10}^0}}} = {{\sqrt 3 } \over {16}}$ $= {{{{\sqrt 3 } \over {16}}\sin {{80}^0}} \over {cos{{10}^0}}} = {{\sqrt 3 } \over {16}}$

Bài 32 trang 196 Sách bài tập (SBT) Toán Đại số 10

Cho ${0^0} < \alpha < {90^0}$ ${0^0} < \alpha < {90^0}$

a) Có giá trị nào của $\alpha$ $\alpha$ sao cho $\tan \alpha < \sin \alpha$ $\tan \alpha < \sin \alpha$ hay không?

b) Chứng minh rằng $\sin \alpha + \cos \alpha > 1$ $\sin \alpha + \cos \alpha > 1$

Gợi ý làm bài

a) Với ${0^0} < \alpha < {90^0}$ ${0^0} < \alpha < {90^0}$ thì $0 < \cos \alpha < 1$ $0 < \cos \alpha < 1$ hay ${1 \over {\cos \alpha }} > 1$ ${1 \over {\cos \alpha }} > 1$

Nhân hai vế với $\sin \alpha > 0$ $\sin \alpha > 0$ ta được $tan\alpha > \sin \alpha$ $tan\alpha > \sin \alpha$

Vậy không có giá trị nào của $\alpha ({0^0} < \alpha < {90^0})$ $\alpha ({0^0} < \alpha < {90^0})$ để $tan\alpha < \sin \alpha$ $tan\alpha < \sin \alpha$

b) Ta có $\sin \alpha + \cos \alpha > 0$ $\sin \alpha + \cos \alpha > 0$ và $\sin \alpha \cos \alpha > 0$ $\sin \alpha \cos \alpha > 0$. Do đó

(sinα+cosα)²=sin²α+cos²α+2sinαcosα

=1+2sinαcosα>1

Từ đó suy ra: $\sin \alpha + \cos \alpha > 1$ $\sin \alpha + \cos \alpha > 1$

Bài 33 trang 196 Sách bài tập (SBT) Toán Đại số 10

Tính các giá trị lượng giác của góc $\alpha$ $\alpha$, biết

a) $\cos \alpha = 2\sin \alpha$ $\cos \alpha = 2\sin \alpha$ khi $0 < \alpha < {\pi \over 2}$ $0 < \alpha < {\pi \over 2}$

b) $\cot \alpha = 4\tan \alpha$ $\cot \alpha = 4\tan \alpha$ khi ${\pi \over 2} < \alpha < \pi$ ${\pi \over 2} < \alpha < \pi$

Gợi ý làm bài

a) Với $0 < \alpha < {\pi \over 2}$ $0 < \alpha < {\pi \over 2}$ thì $\cos \alpha > 0,\sin \alpha > 0$ $\cos \alpha > 0,\sin \alpha > 0$. Ta có

$1 - {\sin ^2}\alpha = {\cos ^2}\alpha$ $1 - {\sin ^2}\alpha = {\cos ^2}\alpha$

Mặt khác ${\cos ^2}\alpha = {(2\sin \alpha )^2} = 4{\sin ^2}\alpha$ ${\cos ^2}\alpha = {(2\sin \alpha )^2} = 4{\sin ^2}\alpha$ nên $5{\sin ^2}\alpha = 1$ $5{\sin ^2}\alpha = 1$ hay

sinα= $\frac{1}{\sqrt{5}}$ $\frac{1}{\sqrt{5}}$, cosα= $\frac{2}{\sqrt{5}}$ $\frac{2}{\sqrt{5}}$

tanα= $\frac{1}{2}$ $\frac{1}{2}$, cotα=2

b) Với ${\pi \over 2} < \alpha < \pi$ ${\pi \over 2} < \alpha < \pi$ thì $\sin \alpha > 0,cos\alpha {\rm{ < 0,tan}}\alpha {\rm{ < 0}}$ $\sin \alpha > 0,cos\alpha {\rm{ < 0,tan}}\alpha {\rm{ < 0}}$

Ta có: $\cot \alpha = 4\tan \alpha = > {1 \over {\tan \alpha }} = 4\tan \alpha$ $\cot \alpha = 4\tan \alpha = > {1 \over {\tan \alpha }} = 4\tan \alpha$

$= > {\tan ^2}\alpha = {1 \over 4} = > \tan \alpha = - {1 \over 2},\cot \alpha = - 2$ $= > {\tan ^2}\alpha = {1 \over 4} = > \tan \alpha = - {1 \over 2},\cot \alpha = - 2$

$\cos \alpha = - {1 \over {\sqrt {1 + {1 \over 4}} }} = - {2 \over {\sqrt 5 }},\sin \alpha = {1 \over {\sqrt 5 }}$ $\cos \alpha = - {1 \over {\sqrt {1 + {1 \over 4}} }} = - {2 \over {\sqrt 5 }},\sin \alpha = {1 \over {\sqrt 5 }}$

Bài 34 trang 196 Sách bài tập (SBT) Toán Đại số 10

Chứng minh các đẳng thức

a) $\tan 3\alpha - \tan 2\alpha - \tan \alpha = \tan \alpha \tan 2\alpha \tan 3\alpha$ $\tan 3\alpha - \tan 2\alpha - \tan \alpha = \tan \alpha \tan 2\alpha \tan 3\alpha$

b) ${{4\tan \alpha (1 - {{\tan }^2}\alpha )} \over {{{(1 + {{\tan }^2}\alpha )}^2}}} = \sin 4\alpha$ ${{4\tan \alpha (1 - {{\tan }^2}\alpha )} \over {{{(1 + {{\tan }^2}\alpha )}^2}}} = \sin 4\alpha$

c) ${{1 + {{\tan }^4}\alpha } \over {{{\tan }^2}\alpha + {{\cot }^2}\alpha }} = {\tan ^2}\alpha$ ${{1 + {{\tan }^4}\alpha } \over {{{\tan }^2}\alpha + {{\cot }^2}\alpha }} = {\tan ^2}\alpha$

d) ${{\cos \alpha \sin (\alpha - 3) - \sin \alpha \cos (\alpha - 3)} \over {\cos (3 - {\pi \over 6}) - {1 \over 2}\sin 3}} = - {{2\tan 3} \over {\sqrt 3 }}$ ${{\cos \alpha \sin (\alpha - 3) - \sin \alpha \cos (\alpha - 3)} \over {\cos (3 - {\pi \over 6}) - {1 \over 2}\sin 3}} = - {{2\tan 3} \over {\sqrt 3 }}$

Gợi ý làm bài

a) $\tan 3\alpha - \tan 2\alpha - \tan \alpha = \tan (2\alpha + \alpha ) - \tan (2\alpha + \alpha )$ $\tan 3\alpha - \tan 2\alpha - \tan \alpha = \tan (2\alpha + \alpha ) - \tan (2\alpha + \alpha )$

$= {{\tan 2\alpha + \tan \alpha } \over {1 - \tan 2\alpha \tan \alpha }} - (\tan 2\alpha + tan\alpha )$ $= {{\tan 2\alpha + \tan \alpha } \over {1 - \tan 2\alpha \tan \alpha }} - (\tan 2\alpha + tan\alpha )$

$= (\tan 2\alpha + tan\alpha )({1 \over {1 - \tan 2\alpha \tan \alpha }} - 1)$ $= (\tan 2\alpha + tan\alpha )({1 \over {1 - \tan 2\alpha \tan \alpha }} - 1)$

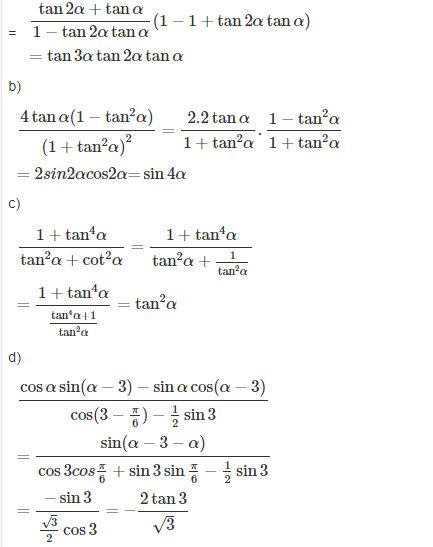
Giải bài tập Toán 10 SBT ôn tập chương 6

Bài 35 trang 197 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng các biểu thức sau là những số không phụ thuộc $\alpha$ $\alpha$

a) $A = 2({\sin ^6}\alpha + c{\rm{o}}{{\rm{s}}^6}\alpha ) - 3({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha )$ $A = 2({\sin ^6}\alpha + c{\rm{o}}{{\rm{s}}^6}\alpha ) - 3({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha )$

b) $A = 4({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha ) - c{\rm{os4}}\alpha$ $A = 4({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha ) - c{\rm{os4}}\alpha$

c) $C = 8(c{\rm{o}}{{\rm{s}}^8}\alpha - {\sin ^8}\alpha ) - \cos 6\alpha - 7\cos 2\alpha$ $C = 8(c{\rm{o}}{{\rm{s}}^8}\alpha - {\sin ^8}\alpha ) - \cos 6\alpha - 7\cos 2\alpha$

Gợi ý làm bài

a) $A = 2({\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha )({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha - {\sin ^2}\alpha co{s^2}\alpha ) - 3({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha )$ $A = 2({\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha )({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha - {\sin ^2}\alpha co{s^2}\alpha ) - 3({\sin ^4}\alpha + c{\rm{o}}{{\rm{s}}^4}\alpha )$

$= - {\sin ^4}\alpha - {\cos ^4}\alpha - 2{\sin ^2}{\cos ^2}\alpha$ $= - {\sin ^4}\alpha - {\cos ^4}\alpha - 2{\sin ^2}{\cos ^2}\alpha$

$= - {({\sin ^2}\alpha + {\cos ^2}\alpha )^2} = - 1$ $= - {({\sin ^2}\alpha + {\cos ^2}\alpha )^2} = - 1$

b) $A = 4{\rm{[}}{({\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha )^2} - 2{\sin ^2}\alpha c{\rm{o}}{{\rm{s}}^2}\alpha {\rm{]}} - c{\rm{os4}}\alpha$ $A = 4{\rm{[}}{({\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha )^2} - 2{\sin ^2}\alpha c{\rm{o}}{{\rm{s}}^2}\alpha {\rm{]}} - c{\rm{os4}}\alpha$

$= 4\left( {1 - {1 \over 2}{{\sin }^2}2\alpha } \right) - 1 + 2{\sin ^2}2\alpha = 3$ $= 4\left( {1 - {1 \over 2}{{\sin }^2}2\alpha } \right) - 1 + 2{\sin ^2}2\alpha = 3$

c) $C = 8(c{\rm{o}}{{\rm{s}}^4}\alpha - {\sin ^4}\alpha )(c{\rm{o}}{{\rm{s}}^4}\alpha + {\sin ^4}\alpha ) - \cos 6\alpha - 7\cos 2\alpha$ $C = 8(c{\rm{o}}{{\rm{s}}^4}\alpha - {\sin ^4}\alpha )(c{\rm{o}}{{\rm{s}}^4}\alpha + {\sin ^4}\alpha ) - \cos 6\alpha - 7\cos 2\alpha$

$= 8(c{\rm{o}}{{\rm{s}}^2}\alpha - {\sin ^2}\alpha )(c{\rm{o}}{{\rm{s}}^2}\alpha + {\sin ^2}\alpha ){\rm{[}}{(c{\rm{o}}{{\rm{s}}^2}\alpha + {\sin ^2}\alpha )^2}$ $= 8(c{\rm{o}}{{\rm{s}}^2}\alpha - {\sin ^2}\alpha )(c{\rm{o}}{{\rm{s}}^2}\alpha + {\sin ^2}\alpha ){\rm{[}}{(c{\rm{o}}{{\rm{s}}^2}\alpha + {\sin ^2}\alpha )^2}$ $- 2{\sin ^2}\alpha c{\rm{o}}{{\rm{s}}^2}\alpha {\rm{]}} - \cos 6\alpha - 7\cos 2\alpha$ $- 2{\sin ^2}\alpha c{\rm{o}}{{\rm{s}}^2}\alpha {\rm{]}} - \cos 6\alpha - 7\cos 2\alpha$

$= 8c{\rm{os}}2\alpha \left( {1 - {1 \over 2}si{n^2}2\alpha } \right) - c{\rm{os6}}\alpha {\rm{ - 7cos2}}\alpha$ $= 8c{\rm{os}}2\alpha \left( {1 - {1 \over 2}si{n^2}2\alpha } \right) - c{\rm{os6}}\alpha {\rm{ - 7cos2}}\alpha$

$= c{\rm{os}}2\alpha - 4\cos 2\alpha si{n^2}2\alpha - c{\rm{os(4}}\alpha + {\rm{2}}\alpha )$ $= c{\rm{os}}2\alpha - 4\cos 2\alpha si{n^2}2\alpha - c{\rm{os(4}}\alpha + {\rm{2}}\alpha )$

$= c{\rm{os}}2\alpha - 2\sin 4\alpha sin2\alpha - c{\rm{os4}}\alpha c{\rm{os2}}\alpha + \sin 4\alpha sin2\alpha$ $= c{\rm{os}}2\alpha - 2\sin 4\alpha sin2\alpha - c{\rm{os4}}\alpha c{\rm{os2}}\alpha + \sin 4\alpha sin2\alpha$

$= c{\rm{os}}2\alpha - (\cos 4\alpha \cos 2\alpha + \sin {\rm{4}}\alpha \sin {\rm{2}}\alpha )$ $= c{\rm{os}}2\alpha - (\cos 4\alpha \cos 2\alpha + \sin {\rm{4}}\alpha \sin {\rm{2}}\alpha )$

$= \cos 2\alpha - c{\rm{os2}}\alpha {\rm{ = 0}}$ $= \cos 2\alpha - c{\rm{os2}}\alpha {\rm{ = 0}}$

Bài 36 trang 197 Sách bài tập (SBT) Toán Đại số 10

Rút gọn các biểu thức

a) ${{\tan 2\alpha } \over {\tan 4\alpha - \tan 2\alpha }}$ ${{\tan 2\alpha } \over {\tan 4\alpha - \tan 2\alpha }}$

b) $\sqrt {1 + \sin \alpha } - \sqrt {1 - \sin \alpha }$ $\sqrt {1 + \sin \alpha } - \sqrt {1 - \sin \alpha }$ với $0 < \alpha < {\pi \over 2}$ $0 < \alpha < {\pi \over 2}$

c) ${{3 - 4\cos 2\alpha + c{\rm{os4}}\alpha } \over {3 + 4\cos 2\alpha + \cos 4\alpha }}$ ${{3 - 4\cos 2\alpha + c{\rm{os4}}\alpha } \over {3 + 4\cos 2\alpha + \cos 4\alpha }}$

d) ${{\sin \alpha + \sin 3\alpha + \sin 5\alpha } \over {\cos \alpha + \cos 3\alpha + c{\rm{os5}}\alpha }}$ ${{\sin \alpha + \sin 3\alpha + \sin 5\alpha } \over {\cos \alpha + \cos 3\alpha + c{\rm{os5}}\alpha }}$

Gợi ý làm bài

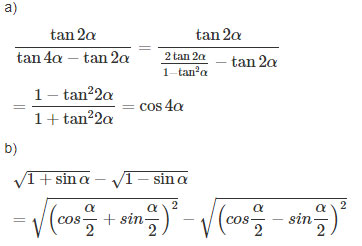
Giải bài tập Toán 10 SBT ôn tập chương 6

Vì $0 < \alpha < {\pi \over 2}$ $0 < \alpha < {\pi \over 2}$ nên $0 < {\alpha \over 2} < {\pi \over 4}$ $0 < {\alpha \over 2} < {\pi \over 4}$

Suy ra $0 < \sin {\alpha \over 2} < \cos {\alpha \over 2}$ $0 < \sin {\alpha \over 2} < \cos {\alpha \over 2}$

Vậy $\sqrt {1 + \sin \alpha } - \sqrt {1 - \sin \alpha } = cos{\alpha \over 2} + sin{\alpha \over 2} - (cos{\alpha \over 2} - sin{\alpha \over 2})$ $\sqrt {1 + \sin \alpha } - \sqrt {1 - \sin \alpha } = cos{\alpha \over 2} + sin{\alpha \over 2} - (cos{\alpha \over 2} - sin{\alpha \over 2})$

$= 2sin{\alpha \over 2}$ $= 2sin{\alpha \over 2}$

c) ${{3 - 4\cos 2\alpha + c{\rm{os4}}\alpha } \over {3 + 4\cos 2\alpha + \cos 4\alpha }}$ ${{3 - 4\cos 2\alpha + c{\rm{os4}}\alpha } \over {3 + 4\cos 2\alpha + \cos 4\alpha }}$ $= {{3 - 4\cos 2\alpha + 2c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha - 1} \over {3 + 4\cos 2\alpha + 2c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha - 1}}$ $= {{3 - 4\cos 2\alpha + 2c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha - 1} \over {3 + 4\cos 2\alpha + 2c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha - 1}}$

$= {{2(c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha - 2\cos 2\alpha + 1)} \over {2(c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha + 2\cos 2\alpha + 1)}}$ $= {{2(c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha - 2\cos 2\alpha + 1)} \over {2(c{\rm{o}}{{\rm{s}}^2}{\rm{2}}\alpha + 2\cos 2\alpha + 1)}}$

$= {{{{(\cos 2\alpha - 1)}^2}} \over {{{(\cos 2\alpha + 1)}^2}}} = {{{{( - 2{{\sin }^2}\alpha )}^2}} \over {{{(2{{\cos }^2}\alpha )}^2}}} = {\tan ^4}\alpha$ $= {{{{(\cos 2\alpha - 1)}^2}} \over {{{(\cos 2\alpha + 1)}^2}}} = {{{{( - 2{{\sin }^2}\alpha )}^2}} \over {{{(2{{\cos }^2}\alpha )}^2}}} = {\tan ^4}\alpha$

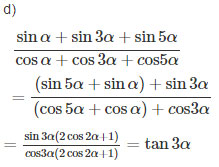
Giải bài tập Toán 10 SBT ôn tập chương 6

Bài 37 trang 197 Sách bài tập (SBT) Toán 10

Cho tam giác ABC không tù, thỏa mãn điều kiện ${\rm{cos2A + 2}}\sqrt 2 \cos B + 2\sqrt 2 \cos C = 3$ ${\rm{cos2A + 2}}\sqrt 2 \cos B + 2\sqrt 2 \cos C = 3$

Hướng dẫn

Giả thiết tam giác ABC không tù có nghĩa là các góc của tam giác nhỏ hơn hoặc bằng ${\pi \over 2}$ ${\pi \over 2}$ và hiệu của hai góc cũng nằm trong khoảng từ $- {\pi \over 2}$ $- {\pi \over 2}$ đến ${\pi \over 2}$ ${\pi \over 2}$. Do đó với $A \le {\pi \over 2}$ $A \le {\pi \over 2}$ thì $\cos {A \over 2} \ge \cos {\pi \over 4} = {{\sqrt 2 } \over 2}$ $\cos {A \over 2} \ge \cos {\pi \over 4} = {{\sqrt 2 } \over 2}$ còn với $- {\pi \over 2} < B - C < {\pi \over 2}$ $- {\pi \over 2} < B - C < {\pi \over 2}$thì $- {\pi \over 4} < {{B - C} \over 2} < {\pi \over 4}$ $- {\pi \over 4} < {{B - C} \over 2} < {\pi \over 4}$ do đó $\cos {{B - C} \over 2} > 0$ $\cos {{B - C} \over 2} > 0$

Giải chi tiết

Ta có

$\cos 2A + 2\sqrt 2 (\cos B + \cos C) = 3$ $\cos 2A + 2\sqrt 2 (\cos B + \cos C) = 3$

$\Leftrightarrow 1 - 2si{n^2}A + 4\sqrt 2 \cos {{B + C} \over 2}\cos {{B - C} \over 2} = 3$ $\Leftrightarrow 1 - 2si{n^2}A + 4\sqrt 2 \cos {{B + C} \over 2}\cos {{B - C} \over 2} = 3$

$\Leftrightarrow 1 - 2si{n^2}A + 4\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} = 3$ $\Leftrightarrow 1 - 2si{n^2}A + 4\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} = 3$

$\Leftrightarrow 2si{n^2}A - 4\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} + 2 = 0$ $\Leftrightarrow 2si{n^2}A - 4\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} + 2 = 0$

$\Leftrightarrow si{n^2}A - 2\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} + 1 = 0$ $\Leftrightarrow si{n^2}A - 2\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} + 1 = 0$

Tam giác ABC không tù nên $\cos {A \over 2} \ge {{\sqrt 2 } \over 2}$ $\cos {A \over 2} \ge {{\sqrt 2 } \over 2}$, suy ra $\sqrt 2 \le 2\cos {A \over 2}$ $\sqrt 2 \le 2\cos {A \over 2}$. Mặt khác, $\cos {{B - C} \over 2} > 0$ $\cos {{B - C} \over 2} > 0$ nên ta có

$2\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} \le 4sin{A \over 2}\cos {A \over 2}\cos {{B - C} \over 2}$ $2\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} \le 4sin{A \over 2}\cos {A \over 2}\cos {{B - C} \over 2}$

Hay $- 2\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} \ge - 2\sin A\cos {{B - C} \over 2}$ $- 2\sqrt 2 sin{A \over 2}\cos {{B - C} \over 2} \ge - 2\sin A\cos {{B - C} \over 2}$

Vì vậy vế trái của (*) $\ge si{n^2}A - 2\sin A\cos {{B - C} \over 2} + 1$ $\ge si{n^2}A - 2\sin A\cos {{B - C} \over 2} + 1$

$= {(\sin A - \cos {{B - C} \over 2})^2} - {\cos ^2}{{B - C} \over 2} + 1$ $= {(\sin A - \cos {{B - C} \over 2})^2} - {\cos ^2}{{B - C} \over 2} + 1$

$= {(\sin A - \cos {{B - C} \over 2})^2} + {\sin ^2}{{B - C} \over 2} \ge 0$ $= {(\sin A - \cos {{B - C} \over 2})^2} + {\sin ^2}{{B - C} \over 2} \ge 0$

Dấu đẳng thức xảy ra khi và chỉ khi $\left\{ \matrix{B - C = 0 \hfill \cr \sin A = \cos {{B - C} \over 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{B = C \hfill \cr \sin A = 1 \hfill \cr} \right.$ $\left\{ \matrix{B - C = 0 \hfill \cr \sin A = \cos {{B - C} \over 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{B = C \hfill \cr \sin A = 1 \hfill \cr} \right.$ $\Leftrightarrow A = {\pi \over 2},B = C = {\pi \over 4}$ $\Leftrightarrow A = {\pi \over 2},B = C = {\pi \over 4}$

Vậy ABC là tam giác vuông cân.

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

120