Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

Các định nghĩa

Toán 10 - Các định nghĩa

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học, tài liệu kèm theo đáp án sẽ là nguồn thông tin hữu ích để giúp các bạn học sinh học tập môn Toán 10 một cách tốt nhất.

Giải bài tập Toán 10 SBT bài 2 chương 6

Giải bài tập Toán 10 SBT bài 3 chương 6

Giải bài tập Toán 10 SBT ôn tập chương 6

Giải bài tập Toán 10 SBT bài 1

Bài 1.1 trang 12 Sách bài tập (SBT) Toán Hình học 10

Hãy tính số các vec tơ (khác $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau:

a) Hai điểm

b) Ba điểm;

c) Bốn điểm.

Gợi ý làm bài

a) Với hai điểm A, B có hai vec tơ $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$, $\underset{BA}{\rightarrow}$ $\underset{BA}{\rightarrow}$

b) Với ba điểm A, B, C có 6 vec tơ $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$, $\underset{BA}{\rightarrow}$ $\underset{BA}{\rightarrow}$, $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$, $\underset{CA}{\rightarrow}$ $\underset{CA}{\rightarrow}$, $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$, $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$

c) Với bốn điểm A, B, C, D có 12 véc tơ (học sinh tự liệt kê).

Bài 1.2 trang 12 Sách bài tập (SBT) Toán Hình học 10

Cho hình vuông ABCD có tâm O. Liệt kê tất cả các vec tơ bằng nhau (khác $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.

Gợi ý làm bài

(h 1.34)

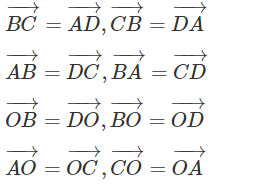
Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

Bài 1.3 trang 12 Sách bài tập (SBT) Toán Hình học 10

Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh $\underset{NP}{\rightarrow}$ $\underset{NP}{\rightarrow}$= $\underset{MQ}{\rightarrow}$ $\underset{MQ}{\rightarrow}$ và $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$= $\underset{NM}{\rightarrow}$ $\underset{NM}{\rightarrow}$

Gợi ý làm bài

(h. 1.35)

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

MN = PQ và MN // PQ

Vì chúng đều bằng $\frac{1}{2}$ $\frac{1}{2}$ AC và đều song song với AC .

Vậy tứ giác MNPQ là hình bình hành nên ta có:

$\underset{NP}{\rightarrow}$ $\underset{NP}{\rightarrow}$= $\underset{MQ}{\rightarrow}$ $\underset{MQ}{\rightarrow}$, $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$= $\underset{NM}{\rightarrow}$ $\underset{NM}{\rightarrow}$

Bài 1.4 trang 12 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm của các cạnh AB và AC. So sánh độ dài của hai vec tơ $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$ và $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$. Vì sao có thể nói hai vec tơ này cùng phương?

Gợi ý làm bài

(h. 1. 36)

MN // BC và MN = $\frac{1}{2}$ $\frac{1}{2}$ hay $\left | \vec{MN} \right |$ $\left | \vec{MN} \right |$ $=\frac{1}{2}$ $=\frac{1}{2}$ $\left | \vec{BC} \right |$ $\left | \vec{BC} \right |$

Vì MN // BC nên $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$ và $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$ cùng phương

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

Bài 1.5 trang 12 Sách bài tập (SBT) Toán Hình học 10

Cho tứ giác ABCD, chứng minh rằng $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ = $\underset{DC}{\rightarrow}$ $\underset{DC}{\rightarrow}$ thì $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$ = $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$

Gợi ý làm bài

(h. 1.37)

Tứ giác ABCD có $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ = $\underset{DC}{\rightarrow}$ $\underset{DC}{\rightarrow}$ nên AB = DC và AB // DC. Do đó ABCD là hình bình hành, suy ra:

$\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$ = $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

Bài 1.6 trang 12 Sách bài tập (SBT) Toán Hình học 10

Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau:

a) $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$cùng hướng, $\left | \vec{AB} \right |> \left | \vec{AC} \right |$ $\left | \vec{AB} \right |> \left | \vec{AC} \right |$

b) $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ ngược hướng

c) $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ cùng phương

Gợi ý làm bài

a) Nếu $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ cùng hướng, $\left | \vec{AB} \right |> \left | \vec{AC} \right |$ $\left | \vec{AB} \right |> \left | \vec{AC} \right |$ thì điểm C nằm giữa hai điểm A và B (h.1.38)

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học
b) Nếu $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ ngược hướng thì điểm A nằm giữa hai điểm B và C (h. 1.39)

c) Nếu $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.

Trường hợp $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ cùng hướng

- Nếu $\left | \vec{AB} \right |> \left | \vec{AC} \right |$ $\left | \vec{AB} \right |> \left | \vec{AC} \right |$ thì C nằm giữa A và B.

- Nếu $\left | \vec{AB} \right |< \left | \vec{AC} \right |$ $\left | \vec{AB} \right |< \left | \vec{AC} \right |$ thì B nằm giữa A và C.

Trường hợp Trường hợp $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ cùng hướng ngược hướng thì A nằm giữa B và C.

Bài 1.7 trang 12 Sách bài tập (SBT) Toán 10

Cho hình bình hành ABCD. Dựng $\underset{AM}{\rightarrow}$ $\underset{AM}{\rightarrow}$ = $\underset{BA}{\rightarrow}$ $\underset{BA}{\rightarrow}$, $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$ = $\underset{DA}{\rightarrow}$ $\underset{DA}{\rightarrow}$, $\underset{NP}{\rightarrow}$ $\underset{NP}{\rightarrow}$= $\underset{DC}{\rightarrow}$ $\underset{DC}{\rightarrow}$, $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$= $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$. Chứng minh rằng $\underset{AQ}{\rightarrow}$ $\underset{AQ}{\rightarrow}$ = $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$

Gợi ý làm bài

(h.1.40)

Giải bài tập Toán 10 SBT bài 1 chương 1 phần Hình học

$\underset{AM}{\rightarrow}$ $\underset{AM}{\rightarrow}$= $\underset{BA}{\rightarrow}$ $\underset{BA}{\rightarrow}$

$\underset{NP}{\rightarrow}$ $\underset{NP}{\rightarrow}$= $\underset{DC}{\rightarrow}$ $\underset{DC}{\rightarrow}$= $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$

Suy ra AM = NP và AM // NP. Vậy tứ giác AMNP là hình bình hành. (1)

Ta có $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$ = $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$

$\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$= $\underset{DA}{\rightarrow}$ $\underset{DA}{\rightarrow}$= $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$

Suy ra PQ = MN và P Q // MN. Vậy tứ giác MNPQ là hình bình hành (2).

Từ (1) và (2) suy ra A = Q hay $\underset{AQ}{\rightarrow}$ $\underset{AQ}{\rightarrow}$ = $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

511