Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Lương Ngọc Quyến - Thái Nguyên lần 2
Đề minh họa Toán 2019
SỞ GD&ĐT THÁI NGUYÊN
TRƯỜNG THPT
LƯƠNG NGỌC QUYẾN
ĐỀ THI THỬ THPTQG LẦN 2 NĂM HỌC 2018 - 2019
Môn:
TOÁN Lớp: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ tên học sinh: ………………….………………………………. Lớp: ........................
Phòng: …….............................................................................. SBD: .......................
Mã đề: 001
Câu 1:
Trong các đẳng thức sau, đẳng thức nào
sai
A.
!
n
Pn
B.
0
1
n
C
C.
!
k
k
n
n
A
C
k
D.
1
n
n
A
Câu 2:
Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng 60°. Thể tích của
khối nón đã cho là
A.
3
3
a
π
.
B.
3
33
a
π
.
C.
3
3
3
a
π
.
D.
3
2
3
a
π
.
Câu 3:
Trong không gian với hệ tọa độ
,Oxyz
cho mặt cầu
2 22
: 6 4 12 0Sx y z x y
. Mặt
phẳng nào sau đây cắt
S
theo một đường tròn có bán kính
3r
A.
2 2 12 0.x yz
B.
3 4 5 17 20 2 0.xyz
C.
3 0.
xyz
D.
4 3 4 26 0.x yz
Câu 4:
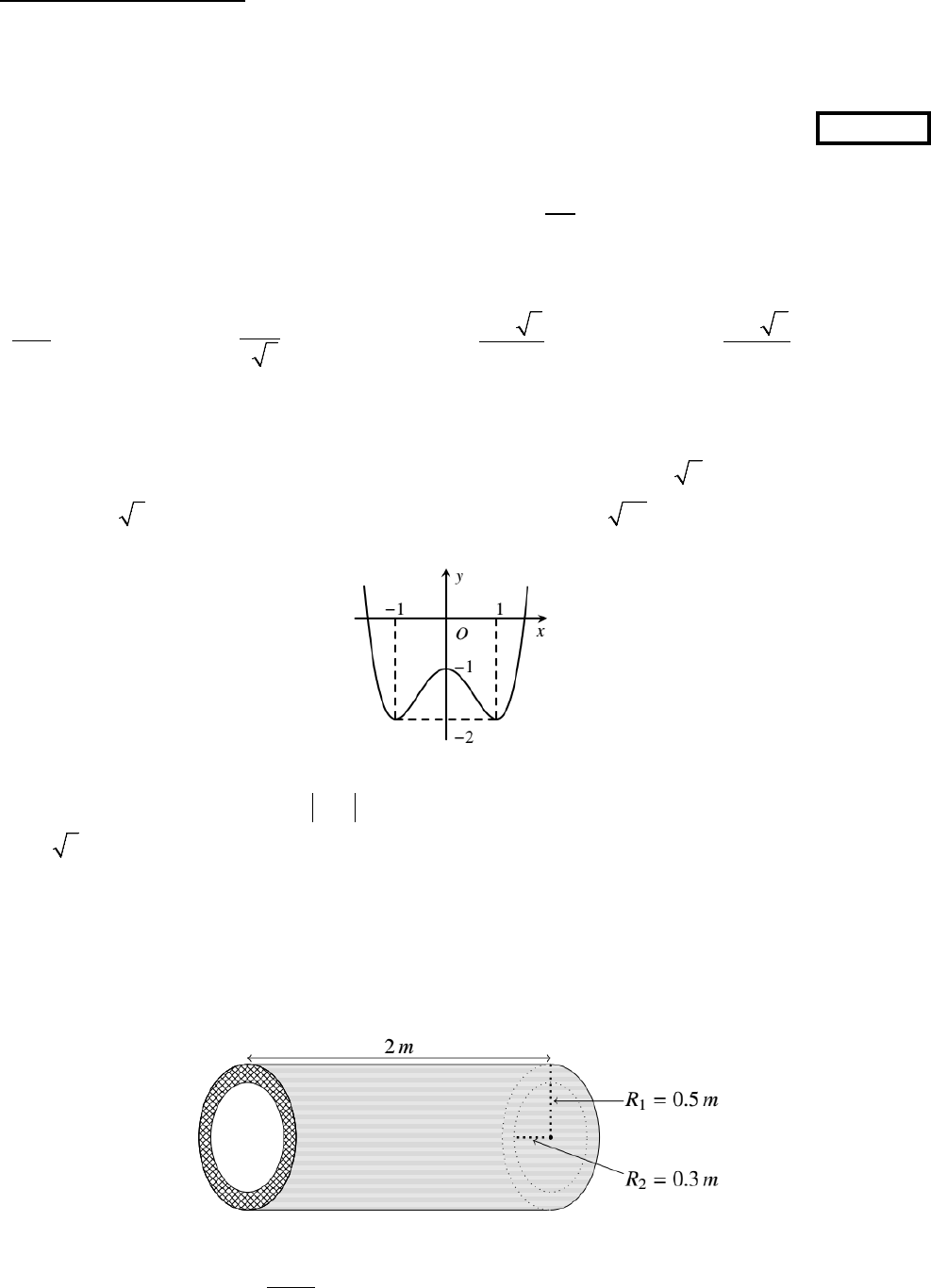
Cho hàm số có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng
A.
–1.
B.
1.
C.
–2.
D.
0.
Câu 5:
Cho các số phức
z
thỏa mãn
12z +=
. Biết rằng tập hợp các điểm biểu diễn các số phức
( )
18w i zi=++
là một đường tròn. Bán kính
r
của đường tròn đó là
A.
9
.
B.
6
.
C.
36
.
D.
3
.
Câu 6:
Trong không gian Oxyz, mặt phẳng
( )
Oxy
có phương trình là
A.
0x =
.
B.
0xy
+=
.
C.
0z =
.
D.
0y
=
.
Câu 7:
Người ta đổ một cái cống bằng cát, đá, xi măng và sắt thép như hình vẽ bên dưới. Thể tích nguyên
vật liệu cần dùng là
A.
0,32π.
B.
0,34π.
C.
0,16π.
D.
0,4π.
Câu 8:
Cho hàm số
3
2
x
y fx
x
có đồ thị
C
. Phương trình tiếp tuyến của đồ thị hàm số tại điểm
có tung độ
0
4y
là
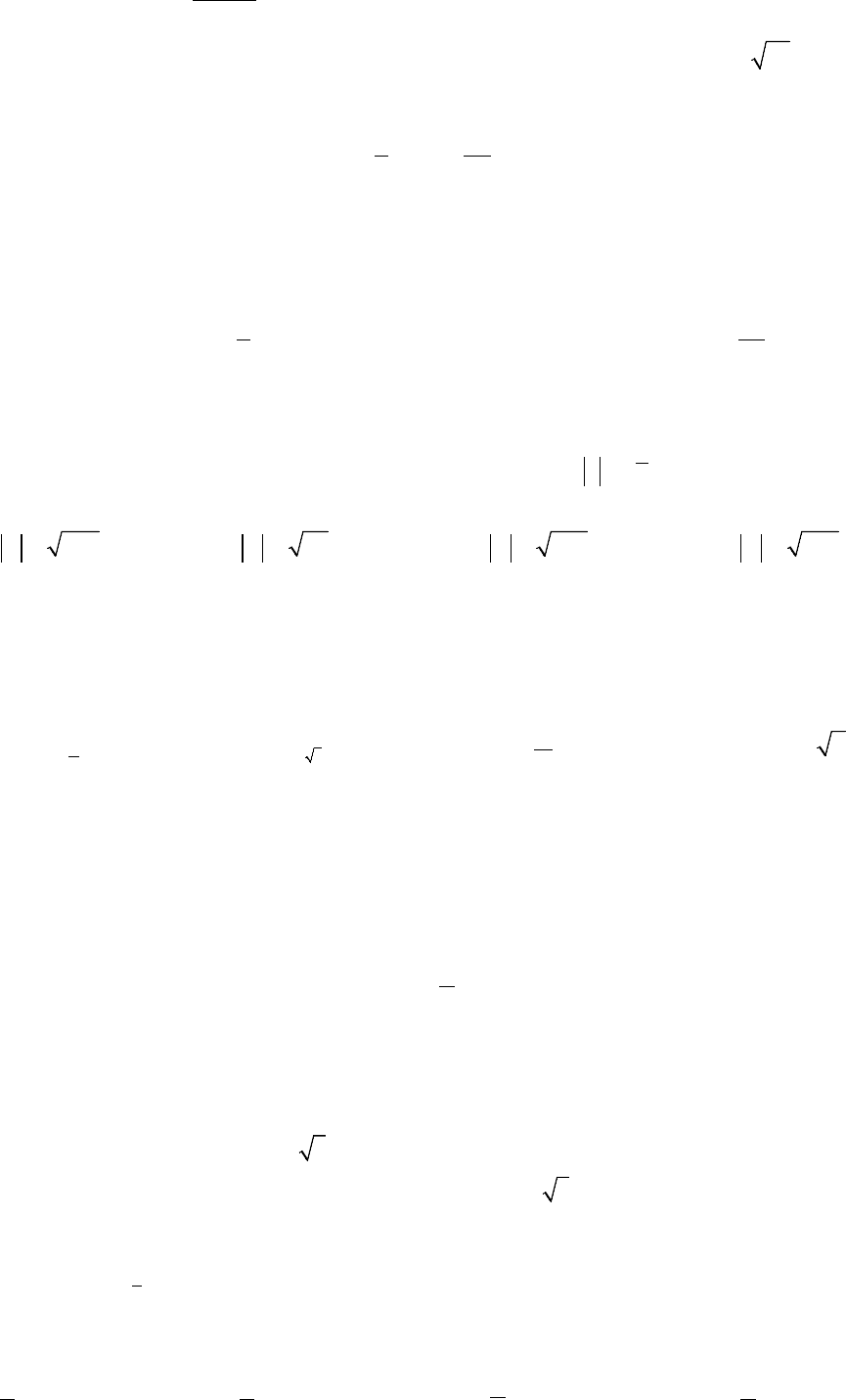
A.
5 10xy− +=
.
B.
5 10xy+ +=
.
C.
5 10xy+ −=
.
D.
5 10xy+ −=
.
Câu 9:
Cho hàm số
21
1
x
y
x
có đồ thị
C
và đường thẳng
:dy x m
. Tìm tất cả các tham số
m
dương để đường thẳng
d
cắt đồ thị
C
tại hai điểm phân biệt
,AB
sao cho
10AB
A.
02mm
.
B.
1m
.
C.
0m
.
D.
2m
.
Câu 10:
Tập nghiệm của bất phương trình
2
2
11
3 27
xx+
>
là
A.
13x<<
.
B.
31
x−< <
.
C.
13x−< <
.
D.
3; 1xx<− >
.
Câu 11:
Biết rằng phương trình:
2
33
log ( 2)log 3 1 0
xm x m− + + −=
có hai nghiệm phân biệt
12
;
xx
thỏa
mãn
12
27xx =
. Khi đó tổng
( )
12
xx
+
bằng
A.
6.
B.
1
3
.
C.
12.
D.
34
3
.
Câu 12:
Tìm tập nghiệm S của phương trình
x1
24
+
=
A.
{ }
S4=
B.
{ }
S3=
C.
{ }
S2=
D.
{ }
S1=
Câu 13:
Cho số phức
z
có phần thực là số nguyên và
z
thỏa mãn
2 73z z iz− =−+ +
. Môđun của số
phức
2
1w zz=−+
bằng
A.
457w =
.
B.
37w =
.
C.
445w =
.
D.
425w
=
.
Câu 14:
Cho phương trình:
32 2
23
2 2 30
x x xm x x
x xm
+−+ +
− +− +=
. Tập các giá trị
m
để phương trình có 3
nghiệm phân biệt có dạng
( )
;ab
. Tổng
( )
2ab+
bằng
A.
2−
.
B.
0.
C.
1.
D.
2.
Câu 15:
Hàm số nào dưới đây nghịch biến trên tập xác định của nó
A.
4
logyx=
π
.
B.
3
logyx
=
.
C.
3
x
y
=
π
.
D.
( )
2
log 1yx= +
.
Câu 16:
Trong không gian Oxyz, cho hai điểm
( )
1; 2; 3A
và
( )
3; 2;1B
. Phương trình mặt cầu đường kính
AB là
A.
( ) (
)
22
2
1 14x yz
− ++− =
.
B.
( ) (
) (
)
2 22
2 2 22xyz−+−+−=
.
C.
2 22
2
xyz++=
.
D.
( ) ( ) ( )
2 22
2 2 24xyz−+−+−=
.
Câu 17:
Một vật chuyển động theo quy luật
32
1
6,
3
s tt
với
t
(giây) là khoảng thời gian tính từ lúc
vật bắt đầu chuyển động và
s
(mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian
10
giây, kể từ lúc bắt đầu chuyển động tại thời điểm
t
bằng bao nhiêu giây thì vận tốc
của vật đạt giá trị lớn nhất
A.
3t
B.
10t
C.
6
t
D.
5t
Câu 18:
Một mặt cầu có bán kính R
3
thì có diện tích bằng
A.
2
12 Rπ
B.
2
4Rπ
C.
2
4R 3π
D.
2
8Rπ
Câu 19:
Cho
2
cosx
0
sin sinI e x xdx a be c
, (a, b, c là các số hữu tỉ). Tính
abc
A.
6
5
B.
3
5
C.
2
3
D.
1
4
Câu 20:
Cho
13
1
2019
f x dx
. Tính
4
0
31f x dx
A.
6057
.
B.
2019
.
C.
673
.
D.
2019−
.
Câu 21:
Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm
A( 2; 4)−
và
B(8; 4)
. Tìm tọa độ điểm C trên
trục Ox, có hoành độ dương sao cho tam giác ABC vuông tại C
A.
C(6;0)
B.
C(3; 0)
C.
C(5;0)
D.
C(1; 0)
Câu 22:
Cho dãy số
n
u
là cấp số nhân với
1
2, 2.uq
Tính
6
u
A.
12
.
B.
32
.
C.
128
.
D.
64
.
Câu 23:
Cho hàm số
(
)
y fx=
liên tục trên
[ ]
1; 3−
và có đồ thị như hình vẽ. Gọi M và m lần lượt là giá
trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên
[ ]
1; 3−
. Giá trị
Mm+
bằng
A.
2.
B.
1.
C.
5.
D.
3.
Câu 24:
Tổng diện tích các mặt của một hình lập phương bằng 96. Thể tích của khối lập phương đó là
A.
48
B.
91
C.
84
D.
64
Câu 25:
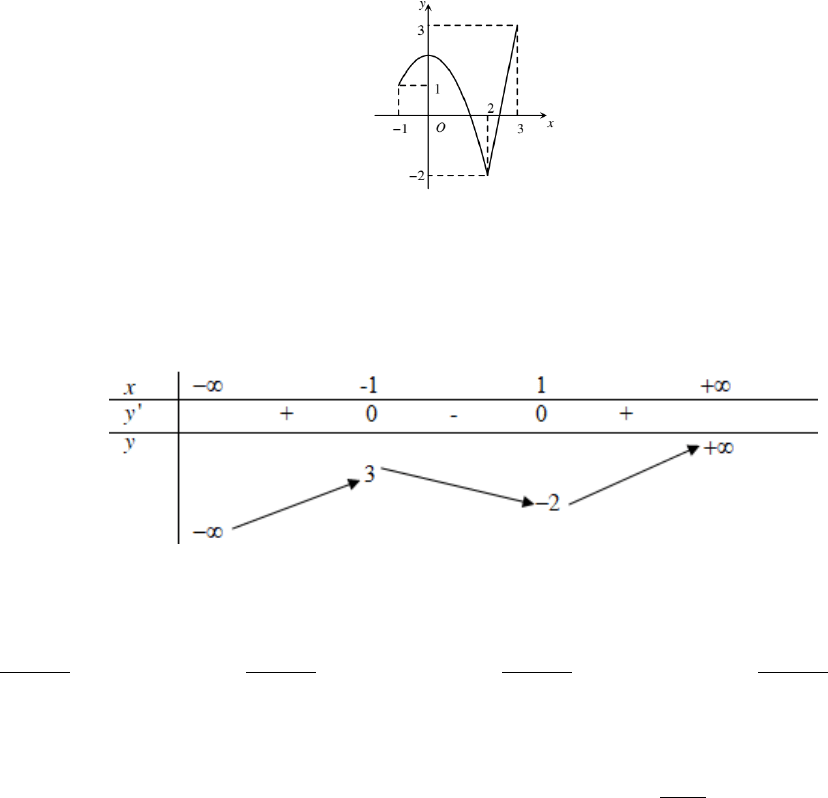
Cho hàm số
( )
y fx=
có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên
khoảng nào dưới đây
A.
( )
1; .+∞
B.
(-1;1).
C.
( )
;1 .−∞
D.
( )
1; .
− +∞
Câu 26:
Đạo hàm của hàm số
( )
2
y ln 5 3x= −
là
A.
2
6x
3x 5
−
−
B.
2
2x
5 3x−
C.
2
6x
3x 5−
D.
2
6
3x 5−
Câu 27:
Trong không gian với hệ trục tọa độ Oxyz cho ba mặt phẳng
(P):x2yz10;(Q):x2yz80;(R):x2yz40− +−= − ++= − +−=
. Một đường thẳng d thay đổi cắt ba
mặt (P), (Q), (R) lần lượt tại A, B, C. Tìm giá trị nhỏ nhất của
2
2
144
T AB
AC
= +
A.
72
B.
144
C.
24
D.
36
Câu 28:
Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm
B(2;1; 3)−
đồng thời
vuông góc với hai mặt phẳng (Q):
x y 3z 0
++ =
, (R):
2x y z 0−+=
là
A.
4x 5y 3z 22 0+−+ =
B.
2x y 3z 14 0+− − =
C.
4x 5y 3z 12 0−−−=
D.
4x 5y 3z 22 0+−− =
Câu 29:
Thể tích của khối hình hộp chữ nhật có các cạnh lần lượt là a, 2a, 3a bằng
A.
3
3a
.
B.
3
6a
.
C.
3
2a
.
D.
3
a
.
Câu 30:
Cho hàm số
( )
y fx=
có đồ thị như hình vẽ dưới đây.
Đề thi thử môn Toán 2019
VnDoc xin giới thiệu tới bạn đọc Đề thi trắc nghiệm Toán 12, Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Lương Ngọc Quyến - Thái Nguyên lần 2. Nội dung tài liệu gồm 50 câu hỏi trắc nghiệm, thời gian làm bài 90 phút sẽ giúp các bạn giải Toán 12 nhanh và chính xác hơn. Mời các bạn học sinh tham khảo.
- Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 Sở GD&ĐT Kon Tum
- Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 Sở GD&ĐT Thanh Hóa
- Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Nguyễn Công Trứ - Hà Tĩnh
- Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Tiên Lãng - Hải Phòng
- Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 trường M.V Lômônôxốp - Hà Nội lần 1
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Thanh Thủy - Phú Thọ lần 1
Trên đây VnDoc đã giới thiệu tới bạn đọc Đáp án đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Lương Ngọc Quyến - Thái Nguyên lần 2. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Hóa học, Thi thpt Quốc gia môn Vật Lý, Thi thpt Quốc gia môn Sinh học, Mã trường thpt mà VnDoc tổng hợp và đăng tải.



