Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thanh Chương 3, Nghệ An (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thanh Chương 3, Nghệ An (Lần 1) được VnDoc.com sưu tầm và đăng tải có 9 câu hỏi cùng đáp án đi kèm, đây là đề luyện thi hữu ích dành cho các bạn học sinh, giúp các bạn củng cố và chuẩn bị tinh thần tốt nhất cho kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Nguyễn Huệ, Hà Nội

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Thanh Chương 1, Nghệ An

SỞ GIÁO DỤC VÀ ĐÀO TẠO NGHỆ AN TRƯỜNG THPT THANH CHƯƠNG III Đề gồm 01 trang

KỲ THI THỬ THPT QUỐC GIA 2016 LẦN 1 Môn thi: Toán Thời gian: 180 phút.

Câu 1 (2,0 điểm). Cho hàm số y = -x³ + 3mx + 1 (1).

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1.

b) Tìm m để đồ thị của hàm số (1) có 2 điểm cực trị A, B sao cho tam giác OAB vuông tại O (với O là gốc tọa độ).

Câu 2 (1,0 điểm). Giải phương trình sin2x + 1 = 6sinx + cos2x.

Câu 3 (1,0 điểm). Tính tích phân

Câu 4 (1,0 điểm).

a) Giải phương trình 5^{2x + 1} - 6.5^x + 1 = 0.

b) Một tổ có 5 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh để làm trực nhật. Tính xác suất để 3 học sinh được chọn có cả nam và nữ.

Câu 5 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho điểm A(-4;1;3) và đường thẳng
Viết phương trình mặt phẳng đi qua (P) và vuông góc với đường thẳng d. Tìm tọa độ điểm B thuộc d sao cho AB = √27.

Câu 6 (1,0 điểm). Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB = AC = a, I là trung điểm của SC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với đáy 1 góc bằng 60^o. Tính thể tích khối chóp S.ABC và tính khoảng cách từ điểm I đến mặt phẳng (SAB) theo a.

Câu 7 (1,0 điểm). Trong mặt phẳng Oxy cho tam giác ABC có A(1;4), tiếp tuyến tại A của đường tròn ngoại tiếp tam giác ABC cắt BC tại D, đường phân giác trong của ADB có phương trình x - y + 2 = 0, điểm M(-4;1) thuộc cạnh AC. Viết phương trình đường thẳng AB.

Câu 8 (1,0 điểm). Giải hệ phương trình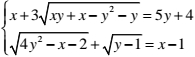

Câu 9 (1,0 điểm). Cho a, b, c là các số dương và a + b + c = 3.

Tìm giá trị lớn nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia 2016 môn Toán

Câu 1. a

Với m=1 hàm số trở thành: y = -x³ + 3x + 1

TXĐ: D = R

y' = -3x² + 3, y' = 0 -> x = ±1

Hàm số nghịch biến trên các khoảng (-;-1) và (1;+), đồng biến trên khoảng (-1;1)

Hàm số đạt cực đại tại x = 1, y_CD = 3, đạt cực tiểu tại x = -1, y_CT = -1

Bảng biến thiên

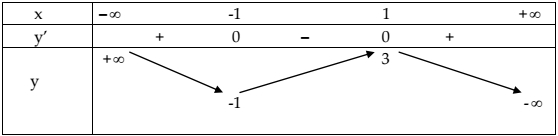
Đồ thị

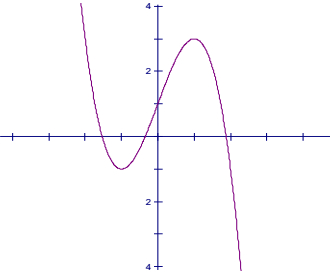
(Còn tiếp)