Đề thi Violympic Toán lớp 9 vòng 17 năm 2015 - 2016
Đề thi Violympic Toán lớp 9 vòng 17
Đề thi Violympic Toán lớp 9 vòng 17 năm 2015 - 2016 là đề thi giải Toán qua mạng có đáp án đi kèm, hi vọng giúp các em học sinh ôn tập và củng cố kiến thức, nhằm đạt kết quả cao trong các vòng tiếp theo của cuộc thi Violympic giải Toán qua mạng năm học 2015 - 2016.
Đề thi Violympic Toán lớp 9 vòng 15 năm 2015 - 2016
Đề thi Violympic Toán lớp 9 vòng 16 năm 2015 - 2016
Đề thi Violympic Toán lớp 9 vòng 17 năm 2015 - 2016 trực tuyến
Bài 1: Vượt chướng ngại vật
Câu 1.1: Cho hàm số y = ax2 có đồ thị là (P). Để (P) cắt đường thẳng (d): y = 2x + 3 tại điểm có tung độ là 1 thì giá trị của a = ......
Câu 1.2: Cho đường tròn (O; R = 6cm). Từ điểm M cách O một khoảng 2R kẻ 2 tiếp tuyến MA, MB với đường tròn (O) (A, B là 2 tiếp điểm). Bán kính đường tròn nội tiếp tam giác MAB có độ dài là ....cm.
Câu 1.3: Cho đường thẳng (d): y = 2x - 3 và parabol (P): y = -x2 cắt nhau tại 2 điểm M và N. Khoảng cách MN = √a (đvđd). Vậy a = ......
Câu 1.4: Cho biểu thức: 
. Để A nguyên dương thì giá trị nhỏ nhất của x = .............
Câu 1.5: Cho a, b, c là 3 số thực dương thỏa mãn abc = 1.
Giá trị nhỏ nhất của biểu thức
là: ............
Bài 2: Hãy điền số thích hợp vào chỗ chấm
Câu 2.1: Để hàm số y = (m2 - 4)x2 + mx - 4 nghịch biến trên R thì m = ..........
Câu 2.2: Cho AB là đường kính của đường tròn (O), bán kính OC vuông góc với AB. Gọi D là điểm trên nửa đường tròn (O) không chứa C sao cho BD = OB. Số đo của cung CAD là ..........o.
Câu 2.3: Giá trị lớn nhất của 
là: ............
Câu 2.4: Điểm A trên đường thẳng y = x và điểm B trên đường thẳng y = 2x cùng có tung độ 6. Diện tích tam giác OAB bằng... (đvdt)
Câu 2.5: Trên mặt phẳng tọa độ Oxy, cho tam giác ABC với tọa độ các đỉnh là A(1; 2); B(3; 4); C(6; 1). Phương trình đường thẳng chứa đường cao AH của tam giác đó có hệ số góc là ..........
Câu 2.6: Phương trình: 
có nghiệm là: x = ..............
Câu 2.7: Điều kiện của m để hệ phương trình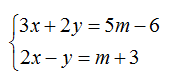 
có nghiệm (x; y) mà x + y < 0 là m < ........
Câu 2.8: Cho tam giác ABC vuông tại A, đường cao AH. Biết chu vi tam giác ABH là 30cm, chu vi tam giác ACH là 40cm. Chu vi tam giác ABC là ..... cm.
Câu 2.9: Cho (x; y) là nghiệm của phương trình 
. Khi đó x + y = ..............
Câu 2.10: Có ....... cặp số tự nhiên (x; y) nằm trong khoảng (1; 500) sao cho x2 + y2 chia hết cho 121.
Bài 3: Cóc vàng tài ba
Câu 3.1: Cho đường thẳng (d1): y = -2x + 3. Phương trình đường thẳng (d2) song song với (d1) và cắt trục tung tại điểm có tung độ bằng -1 là:
a. y = -2x + 1
b. y = 2x + 1
c. y = -2x - 1
d. y = 2x - 1
Câu 3.2: Hai đường thẳng (d1): x + 2y = 2 và (d2): 2x - y + 6 = 0 cắt nhau tại C. (d1) và (d2) cắt Ox lần lượt tại 2 điểm A và B. Diện tích tam giác ABC là ....... (đvdt).
a. 7 b. 5 c. 4 d. 10
Câu 3.3: Gọi x1, x2 là 2 nghiệm của phương trình: x2 - 2kx - (k - 1)(k - 3) = 0. Khi đó 1/4. (x1 + x2)2 + x1.x2 - 2(x1 - x2) = ...
a. 3 b. 4 c. 0 d. -3
Câu 3.4: Cho đường tròn (O; R) nội tiếp hình thoi ABCD cạnh AB = 4√3cm, số đo góc BAD = 120o. Khi đó R = ...... cm.
a. 5 b. 4 c. 6 d. 3
Câu 3.5: Phương trình mx2 - 2(m - 1)x + m + 1 = 0 (1) (m là tham số, m > 0).
Để (1) có 2 nghiệm phân biệt x1, x2 thỏa mãn x12 + x22 = 16 thì m = ........
a. 2/7 b. 3/8 c. 1/3 d. 7/2
Câu 3.6: Cho tam giác ABC vuông tại A, đường cao AH = 12cm, HC = 4HB. Bán kính đường tròn ngoại tiếp tam giác ABC có độ dài là ....cm.
a. 20 b. 32 c. 30 d. 15
Câu 3.7: Cho x, y là các số thực thỏa mãn x2 + y2 - xy = 4. Giá trị lớn nhất của biểu thức A = x2 + y2 bằng:
a. 10 b. 4 c. 6 d. 8
Câu 3.8: Cho tam giác ABC cân tại B. Các đường cao AD và BE cắt nhau tại H. Một đường thẳng (d) đi qua A và vuông góc với AB, cắt BE tại F. Tứ giác AHCF là:
a. Hình vuông
b. Hình chữ nhật
c. Hình thoi
d. Hình thang vuông
Câu 3.9: Cho x, y, z là ba số dương. Giá trị nhỏ nhất của
là:
a. 81 b. 9 c. 12 d. 3
Câu 3.10: Cho 2 đường thẳng (d1): y = 3/4. x + 3 và (d2): y = 3/4 .x - 3. Khoảng cách giữa hai đường thẳng trên là ....... (đvdt)
a. 8,1 b. 9,8 c. 4,8 d. 9,6
Đáp án đề thi Violympic Toán lớp 9 vòng 17
Bài 1: Vượt chướng ngại vật
Câu 1.1: 1
Câu 1.2: 3
Câu 1.3: 80
Câu 1.4: 4
Câu 1.5: 3/2
Bài 2: Hãy điền số thích hợp vào chỗ chấm
Câu 2.1: -2
Câu 2.2: 210
Câu 2.3: 4
Câu 2.4: 9
Câu 2.5: 1
Câu 26: 5
Câu 2.7: 1,5
Câu 2.8: 50
Câu 2.9: 16
Câu 2.10: 2025
Bài 3: Cóc vàng tài ba
Câu 3.1: c
Câu 3.2: b
Câu 3.3: d
Câu 3.4: d
Câu 3.5: a
Câu 3.6: d
Câu 3.7: d
Câu 3.8: c
Câu 3.9: b
Câu 3.10: c
