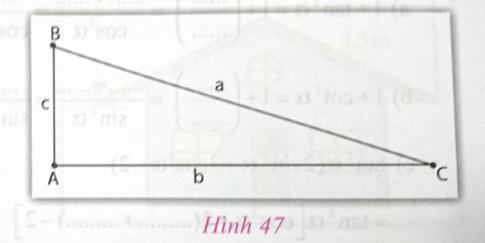
Soạn Toán 9 bài 6 Luyện tập VNEN

Soạn Toán 9 tập 1 phần hình học

VnDoc xin giới thiệu tới các bạn bài Soạn Toán 9 VNEN bài 6 Luyện tập. Tài liệu sẽ giúp các bạn học sinh hệ thống lại những kiến thức đã học trong bài, định hướng phương pháp giải các bài tập cụ thể. Mời các bạn tải về tham khảo

Bài 6 Luyện tập VNEN

C. Hoạt động luyện tập
D.E. Hoạt động vận dụng và tìm tòi, mở rộng
- Câu 2: Trang 80 sách VNEN 9 tập 1

C. Hoạt động luyện tập

Câu 1: Trang 77 sách VNEN 9 tập 1

Cho tam giác ABC vuông tại A, BC = a, AC = b, AB = c (h.47).

Soạn Toán 9 bài 6 Luyện tập VNEN

Giải tam giác vuông trong các trường hợp sau:

a) b = 5cm, c = 12cm;

b) a = 8cm, b = 6cm;

c) b = 6cm, $\widehat{B} = 60^{\circ}$ $\hat{B} = 60^{\circ}$

d) a = 10cm, $\widehat{C} = 25^{\circ}.$ $\hat{C} = 25^{\circ} .$

Bài làm:

Giải câu a) b = 5cm, c = 12cm

$a = \sqrt{b^{2} + c^{2}} = \sqrt{5^{2} + 12^{2}} = 13cm$ $a = \sqrt{b^{2} + c^{2}} = \sqrt{5^{2} + 12^{2}} = 13 c m$

$sin B = \frac{b}{a} = \frac{5}{13} \Rightarrow \widehat{B} = 22,6^{\circ}; \widehat{C} = 90^{\circ} - 22,6^{\circ} = 67,4^{\circ}$ $s i n B = \frac{b}{a} = \frac{5}{13} \Rightarrow \hat{B} = 22, 6^{\circ}; \hat{C} = 90^{\circ} - 22, 6^{\circ} = 67, 4^{\circ}$

Giải câu b) a = 8cm, b = 6cm

$c = \sqrt{a^{2} - b^{2}} = \sqrt{8^{2} - 6^{2}} = 2\sqrt{7}cm$ $c = \sqrt{a^{2} - b^{2}} = \sqrt{8^{2} - 6^{2}} = 2 \sqrt{7} c m$

$sinB = \frac{b}{a} = \frac{6}{8} \Rightarrow \widehat{B} = 48,6^{\circ}; \widehat{C} = 90^{\circ} - 48,6^{\circ} = 41,4^{\circ}$ $s i n B = \frac{b}{a} = \frac{6}{8} \Rightarrow \hat{B} = 48, 6^{\circ}; \hat{C} = 90^{\circ} - 48, 6^{\circ} = 41, 4^{\circ}$

Giải câu c) b = 6cm, $\widehat{B} = 60^{\circ}$ $\hat{B} = 60^{\circ}$

$\widehat{C} = 90^{\circ} - \widehat{B} = 90^{\circ} - 60^{\circ} = 30^{\circ}$ $\hat{C} = 90^{\circ} - \hat{B} = 90^{\circ} - 60^{\circ} = 30^{\circ}$

$sinB = \frac{b}{a} = \frac{6}{a} \Rightarrow a = 4\sqrt{3} cm, c = \sqrt{a^{2} - b^{2}} = \sqrt{(4\sqrt{3})^{2} - 6^{2}} = 2\sqrt{3} cm$ $s i n B = \frac{b}{a} = \frac{6}{a} \Rightarrow a = 4 \sqrt{3} c m, c = \sqrt{a^{2} - b^{2}} = \sqrt{(4 \sqrt{3})^{2} - 6^{2}} = 2 \sqrt{3} c m$

Giải câu d) a = 10cm, $\widehat{C} = 25^{\circ}$ $\hat{C} = 25^{\circ}$

$\widehat{B} = 90^{\circ} - \widehat{C} = 90^{\circ} - 25^{\circ} = 65^{\circ}$ $\hat{B} = 90^{\circ} - \hat{C} = 90^{\circ} - 25^{\circ} = 65^{\circ}$

$sinB = \frac{b}{a} = \frac{b}{10} \Rightarrow b = 9,06 cm, c = \sqrt{a^{2} - b^{2}} = \sqrt{10^{2} - 9,06^{2}} = 4,23 cm.$ $s i n B = \frac{b}{a} = \frac{b}{10} \Rightarrow b = 9, 06 c m, c = \sqrt{a^{2} - b^{2}} = \sqrt{10^{2} - 9, 06^{2}} = 4, 23 c m .$

Câu 2: Trang 78 sách VNEN 9 tập 1

Điền vào chỗ chấm (...) để đơn giản các biểu thức sau:

$a) 1 + tan^{2}\alpha = 1 + (\frac{......}{.....})^{2} = \frac{.....+......}{cos^{2}\alpha} = \frac{.......}{cos^{2}\alpha}$ $a) 1 + t a n^{2} α = 1 + (\frac{. . . . . .}{. . . . .})^{2} = \frac{. . . . . + . . . . . .}{c o s^{2} α} = \frac{. . . . . . .}{c o s^{2} α}$

$b) 1 + cot^{2}\alpha = 1 + (\frac{......}{.....})^{2} = \frac{.....+......}{sin^{2}\alpha} = \frac{.......}{sin^{2}\alpha}$ $b) 1 + c o t^{2} α = 1 + (\frac{. . . . . .}{. . . . .})^{2} = \frac{. . . . . + . . . . . .}{s i n^{2} α} = \frac{. . . . . . .}{s i n^{2} α}$

$c) tan^{2}\alpha (2sin^{2}\alpha + 3cos^{2}\alpha - 2)$ $c) t a n^{2} α (2 s i n^{2} α + 3 c o s^{2} α - 2)$

$= tan^{2}\alpha (cos^{2}\alpha + 2(...........+...........) - 2)$ $= t a n^{2} α (c o s^{2} α + 2 (. . . . . . . . . . . + . . . . . . . . . . .) - 2)$

$= \frac{sin^{2}\alpha}{cos^{2}\alpha}x............=...........$ $= \frac{s i n^{2} α}{c o s^{2} α} x . . . . . . . . . . . . = . . . . . . . . . . .$

Bài làm:

$a) 1 + tan^{2}\alpha$ $a) 1 + t a n^{2} α$

$= 1 + (\frac{sin\alpha}{cos\alpha})^{2}$ $= 1 + (\frac{s i n α}{c o s α})^{2}$

$= \frac{cos^{2}\alpha + sin^{2}\alpha}{cos^{2}\alpha}$ $= \frac{c o s^{2} α + s i n^{2} α}{c o s^{2} α}$

$= \frac{1}{cos^{2}\alpha}.$ $= \frac{1}{c o s^{2} α} .$

$b) 1 + cot^{2}\alpha$ $b) 1 + c o t^{2} α$

$= 1 + (\frac{cos\alpha}{sin\alpha})^{2}$ $= 1 + (\frac{c o s α}{s i n α})^{2}$

$= \frac{cos^{2}\alpha + sin^{2}\alpha}{sin^{2}\alpha}$ $= \frac{c o s^{2} α + s i n^{2} α}{s i n^{2} α}$

$= \frac{1}{sin^{2}\alpha}$ $= \frac{1}{s i n^{2} α}$

$c) tan^{2}\alpha (2sin^{2}\alpha + 3cos^{2}\alpha - 2)$ $c) t a n^{2} α (2 s i n^{2} α + 3 c o s^{2} α - 2)$

$= tan^{2}\alpha (cos^{2}\alpha + 2(sin^{2}\alpha + cos^{2}\alpha ) - 2)$ $= t a n^{2} α (c o s^{2} α + 2 (s i n^{2} α + c o s^{2} α) - 2)$

$= \frac{sin^{2}\alpha}{cos^{2}\alpha}xcos^{2}\alpha = sin^{2}\alpha.$ $= \frac{s i n^{2} α}{c o s^{2} α} x c o s^{2} α = s i n^{2} α .$

Câu 3: Trang 78 sách VNEN 9 tập 1

Tính x, y trong các hình vẽ sau đây:

a) (h.48a)

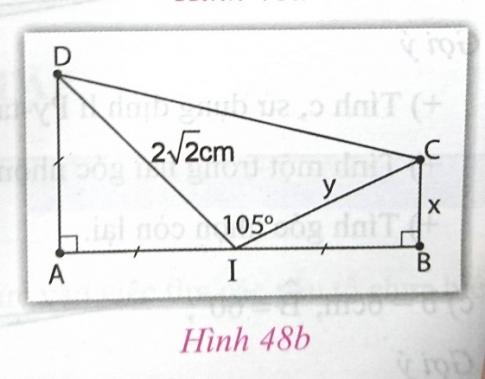
Soạn Toán 9 bài 6 Luyện tập VNEN

b) (h.48b)

Soạn Toán 9 bài 6 Luyện tập VNEN

Bài làm:

$a) cosB = \frac{BH}{AB} = \frac{5}{x} \Rightarrow x = 5\sqrt{2}cm$ $a) c o s B = \frac{B H}{A B} = \frac{5}{x} \Rightarrow x = 5 \sqrt{2} c m$

Tam giác ABH vuông cân nên $A H = B H = 5 c m$

$sinC = \frac{AH}{AC} = \frac{5}{y} \Rightarrow y = 10cm$ $s i n C = \frac{A H}{A C} = \frac{5}{y} \Rightarrow y = 10 c m$

b) * Ta có tam giác ADI là tam giác vuông cân tại A nên $AD = AI = \frac{DI}{\sqrt{2}} = 2cm$ $A D = A I = \frac{D I}{\sqrt{2}} = 2 c m$ và $\widehat{AID} = 45^{\circ} \Rightarrow \widehat{CIB} = 180^{\circ} - 45^{\circ} - 135^{\circ} = 30^{\circ}.$ $\hat{A I D} = 45^{\circ} \Rightarrow \hat{C I B} = 180^{\circ} - 45^{\circ} - 135^{\circ} = 30^{\circ} .$

Theo hình vẽ $I B = A I = 2 c m$

* Ta có:

$cos\widehat{CIB} = \frac{IB}{CI} = \frac{2}{y} \Rightarrow y = \frac{4}{\sqrt{3}} cm$ $c o s \hat{C I B} = \frac{I B}{C I} = \frac{2}{y} \Rightarrow y = \frac{4}{\sqrt{3}} c m$

$x = \sqrt{CI^{2} - IB^{2}} = \sqrt{(\frac{4}{\sqrt{3}})^{2} - 2^{2}} = \frac{2}{\sqrt{3}} cm.$ $x = \sqrt{C I^{2} - I B^{2}} = \sqrt{(\frac{4}{\sqrt{3}})^{2} - 2^{2}} = \frac{2}{\sqrt{3}} c m .$

Câu 4: Trang 78 sách VNEN 9 tập 1

Một người đứng trên một ngọn hải đăng nhìn về phía một chiếc ca-nô trên biển tạo thành một góc $27^{\circ}$ $27^{\circ}$ so với phương nằm ngang. Biết ca-nô cách ngọn hải đăng khoảng 300m. Ước lượng chiều cao của ngọn hải đăng

Soạn Toán 9 bài 6 Luyện tập VNEN

Bài làm:

Chiều cao của ngọn hải đăng chính là đoạn BC

Ta có $\widehat{A} = 27^{\circ}$ $\hat{A} = 27^{\circ}$ (so le trong)

Ta có công thức sau: $tanA = \frac{BC}{AB} \Rightarrow BC = AB.tanA = 300.tan27^{\circ} = 152,9m$ $t a n A = \frac{B C}{A B} \Rightarrow B C = A B . t a n A = 300. t a n 27^{\circ} = 152, 9 m$

Vậy chiều cao ngọn hải đăng là 152,9m.

Câu 5: Trang 79 sách VNEN 9 tập 1

Nam đang học vẽ hình bằng phần mềm trên máy tính. Nam vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (mái hai dốc) như hình 50.

Soạn Toán 9 bài 6 Luyện tập VNEN

Biết rằng góc tạo bởi phần mái và mặt phẳng nằm ngang là $25^{\circ}$ $25^{\circ}$ , chiều dài mỗi bên dốc mái là 3,5m. Tính bề rộng của mái nhà.

Gợi ý: Vẽ lại mô hình mái nhà dưới dạng tam giác cân như sau (h.51):

Soạn Toán 9 bài 6 Luyện tập VNEN

Kẻ đường cao AH. Ta đi tính BH, từ đó tính được BC với lưu ý H là trung điểm của BC.

Bài làm:

Bề rộng của mái nhà chính là đoạn BC.

Kẻ AH vuông góc với BC, vì tam giác ABC cân nên BH = CH

Xét tam giác vuông ABH, ta có:

$cosB = \frac{BH}{AB} \Leftrightarrow cos25^{\circ} = \frac{BH}{3,5} \Rightarrow BH = 3,17m$ $c o s B = \frac{B H}{A B} \Leftrightarrow c o s 25^{\circ} = \frac{B H}{3, 5} \Rightarrow B H = 3, 17 m$

Suy ra BC = 2BH = 6,34m

Vậy bề rộng của mái nhà là 6,34m.

D.E. Hoạt động vận dụng và tìm tòi, mở rộng

Câu 2: Trang 80 sách VNEN 9 tập 1

Bài toán 2: Hai đài quan sát ở hai vị trí cách nhau 60km cùng quan sát một chiếc máy bay đang bay trên bầu trời tạo thành các góc $15^{\circ}$ $15^{\circ}$ và $35^{\circ}$ $35^{\circ}$ so với phương ngang. Tính độ cao của máy bay (h.53).

Soạn Toán 9 bài 6 Luyện tập VNEN

Bài làm:

Vẽ lại mô hình dưới dạng hình tam giác như hình vẽ dưới

Soạn Toán 9 bài 6 Luyện tập VNEN

Gọi các điểm như hĩnh vẽ

Kẻ đường cao AH

Xét tam giác vuông ABH, ta có:

$tanB = \frac{AH}{BH} \Leftrightarrow tan15^{\circ} = \frac{AH}{BH} \Rightarrow BH = \frac{AH}{tan15^{\circ}}$ $t a n B = \frac{A H}{B H} \Leftrightarrow t a n 15^{\circ} = \frac{A H}{B H} \Rightarrow B H = \frac{A H}{t a n 15^{\circ}}$

Xét tam giác vuông ACH, ta có:

$tanC = \frac{AH}{CH} \Leftrightarrow tan35^{\circ} = \frac{AH}{CH} \Rightarrow CH = \frac{AH}{tan35^{\circ}}$ $t a n C = \frac{A H}{C H} \Leftrightarrow t a n 35^{\circ} = \frac{A H}{C H} \Rightarrow C H = \frac{A H}{t a n 35^{\circ}}$

Ta có: $BC = BH + CH = \frac{AH}{tan15^{\circ}} + \frac{AH}{tan35^{\circ}} = AH.(\frac{1}{tan15^{\circ}} + \frac{1}{tan35^{\circ}})$ $B C = B H + C H = \frac{A H}{t a n 15^{\circ}} + \frac{A H}{t a n 35^{\circ}} = A H . (\frac{1}{t a n 15^{\circ}} + \frac{1}{t a n 35^{\circ}})$

$\Rightarrow AH = \frac{BC}{\frac{1}{tan15^{\circ}} + \frac{1}{tan35^{\circ}}} = 11,63 km$ $\Rightarrow A H = \frac{B C}{\frac{1}{t a n 15^{\circ}} + \frac{1}{t a n 35^{\circ}}} = 11, 63 k m$

Vậy độ cao của máy bay là 11,63 km.

Giải bài 6: Luyện tập- Sách VNEN toán 9 tập 1 trang 76. Trên đây VnDoc đã hướng dẫn các bạn soạn Toán 9, lời giải chi tiết dễ hiểu hy vọng sẽ giúp các bạn củng cố thêm kiến thức từ đó vận dụng vào giải các các bài tập Toán lớp 9. Mời các bạn cùng tham khảo

.............................................

Ngoài Soạn Toán 9 bài 6 Luyện tập VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

650

Bài trước

Bài sau

Chia sẻ bởi:
Đinh Thị Nhàn

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!