Bài làm:
Hàm số 
\(y = 10x + 8\) là hàm số bậc nhất
Hàm số \(y = \frac{x}{3} + 2\) là hàm số bậc nhất
Hàm số \(y = \frac{x}{3} + 1\) là hàm số bậc nhất
Hàm số \(y = \frac{17x - 25}{10}\) là hàm số bậc nhất.
Soạn Toán 9 bài 1 Hàm số bậc nhất và đồ thị VNEN
Soạn Toán 9 tập 1
Soạn Toán 9 VNEN bài 1 Hàm số bậc nhất và đồ thị được VnDoc sưu tầm và đăng tải, hy vọng tài liệu này các sẽ giúp ích cho các bạn củng cố lại kiến thức, rèn luyện kĩ năng làm bài Toán 9 tốt hơn. Mời các bạn tải về cùng tham khảo
Bài 1 Hàm số bậc nhất và đồ thị VNEN
A. HOẠT ĐỘNG KHỞI ĐỘNG
Giải quyết bài toán thực tế và trả lời câu hỏi
Bài toán: Một người thợ điện nhận lắp đặt đường dây và thiết bị điện cho một ngôi nhà sắp xây xong phần thô. Người ta đã mua sắm vật liệu hết 20 000 000đồng. Tiền công lắp đặt được trả theo ngày với giá là 350 000 đồng/ngày. Hỏi sau x ngày thợ điện sẽ được thanh toán bao nhiêu tiền (kể cả tiền đã mua sắm vật liệu)?
Hướng dẫn: Gọi t là số tiền mà người thợ điện sẽ được thanh toán sau x ngày làm việc, ta có: t = 350 000.x + 20 000 000.
Trả lời các câu hỏi sau
- Trong bài toán trên, hãy chỉ ra đại lượng nào là hàm số, đại lượng nào là biến số.
- Viết công thức biểu diễn hàm số nói trên và nêu nhận xét về đa thức ở vế phải.
Trả lời:
Gọi t là số tiền mà người thợ điện sẽ được thanh toán sau x ngày làm việc, ta có: t = 350 000.x + 20 000 000.
Vậy sau x ngày làm việc người thợ sẽ được thanh toán 350 000.x + 20 000 000 đồng.
- Trong bài toán trên, đại lượng nào là hàm số là t, biến số là x
- Hàm số: y = 350 000.x + 20 000 000
Hàm số bên phải là phương trình bậc nhất một ẩn.
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
2.b) Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
y = 2x; y = 2x + 3 ; y = 4x ; y = 0,1 - 0,3x.
Trả lời:
Hàm số y = 2x là hàm số bậc nhất.
Hàm số y = 2x + 3 là hàm số bậc nhất.
Hàm số y = 4x không phải là hàm số bậc nhất.
Hàm số y = 0,1 - 0,3x là hàm số bậc nhất.
c) Cho hàm số y = f(x) = 3x - 2. Tìm:
* Giá trị của y khi x bằng 2; -3,5; 1,8; 0.
* Giá trị của x khi giá trị tương ứng của y là 46; -4; 0; 1.
Trả lời:
* Khi x = 2 thì y = f(x) = 3.2 - 2 = 4
Khi x = -3,5 thì y = f(x) = 3.(-3,5) - 2 = -12,5
Khi x = 1,8 thì y = f(x) = 3.1,8 - 2 = 3,4
Khi x = 0 thì y = f(x) = 3.0 - 2 = -2
* Nếu y = f(x) = 3x - 2 = 46, suy ra x = 16
Nếu y = f(x) = 3x - 2 = -4, suy ra x = -23
Nếu y = f(x) = 3x - 2 = 0, suy ra x = 23
Nếu y = f(x) = 3x - 2 = 1, suy ra x = 1
3.b) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
a) y = x - 2 ; b) y = x + 3
Trả lời:
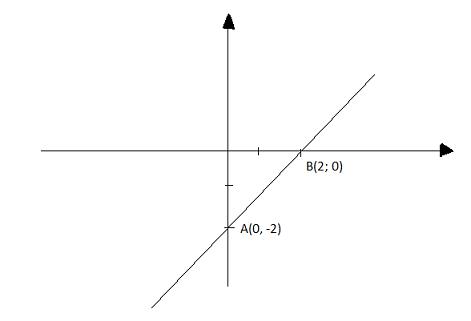
* y = x - 2
Cho x = 0 thì y = -2, ta được điểm A(0; -2)
Cho y = 0 thì x = 2, ta được điểm B(2; 0)
* y = x + 3
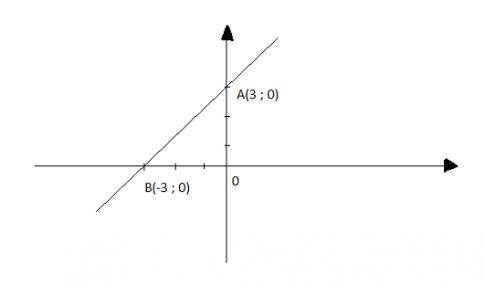
Cho x = 0 thì y = 3, ta được điểm A(0; 3)
Cho y = 0 thì x = - 3, ta được điểm B(-3; 0)
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 37 sách VNEN 9 tập 1
Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
\(y = 10x + 8\); \(y = \frac{x}{3} + 2\); \(y = \frac{x}{3} + 1\); \(y = 2x^{2} + 4\); \(y = \frac{17x - 25}{10}\)
Câu 2: Trang 37 sách VNEN 9 tập 1
Cho hàm số bậc nhất y = 10x + 1. Tìm:
a) Giá trị của y tương ứng với các giá trị của x bằng \(2; -1,5 ; 0; \frac{3}{2}\).
b) Giá trị của x khi giá trị tương ứng của y là \(-9; -4; 6; 31\).
Bài làm:
a) Khi x = 2 thì y = f(x) = 10.2 + 1 = 21
Khi x = -1,5 thì y = f(x) = 10.(-1,5) + 1 = -14
Khi x = 0 thì y = f(x) = 10.0 + 1 = 1
Khi \(x = \frac{3}{2}\) thì \(y = f(x) = 10.\frac{3}{2} + 1 = 16\)
b) Nếu y = f(x) = 10x + 1 = -9, suy ra x = -1
Nếu y = f(x) = 10x + 1 = -4, suy ra x = -0,5
Nếu y = f(x) = 10x + 1 = 6, suy ra x = 0,5
Nếu y = f(x) = 10x + 1 = 31, suy ra x = 3.
Câu 3: Trang 38 sách VNEN 9 tập 1
Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
a) y = \(0,5x - 2\); b) \(y = -2x - 1\); c) \(y = -0,5x + 2\); d) \(y = \frac{1}{3}x - 1\).
Bài làm:
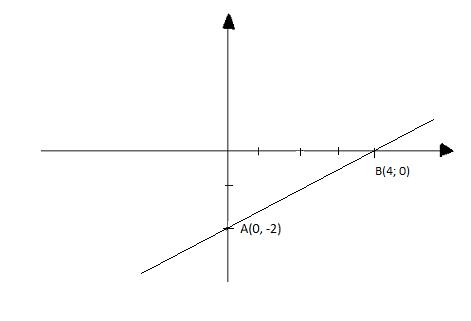
a) y = 0,5x - 2
Cho x = 0 thì y = -2, ta được điểm A(0; -2)
Cho y = 0 thì x = 4, ta được điểm B(4; 0)
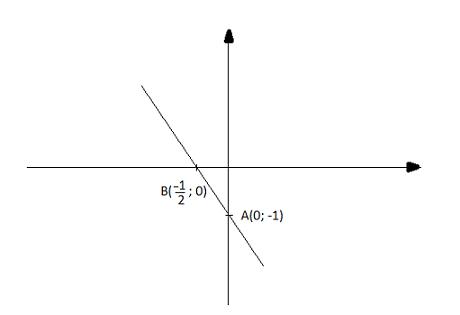
b) y = -2x - 1
Cho x = 0 thì y = -1, ta được điểm A(0; -1)
Cho y = 0 thì \(x = - \frac{1}{2}\), ta được điểm \(B(-\frac{1}{2}; 0)\)
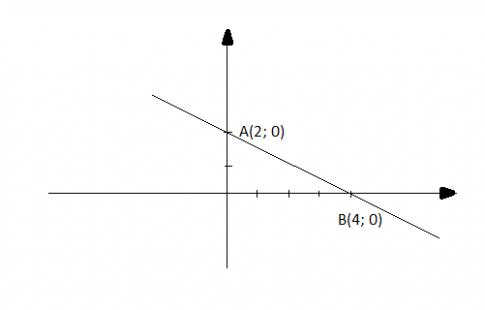
c) y = -0,5x + 2
Cho x = 0 thì y = 2, ta được điểm A(0; 2)
Cho y = 0 thì x = 4, ta được điểm B(4; 0)
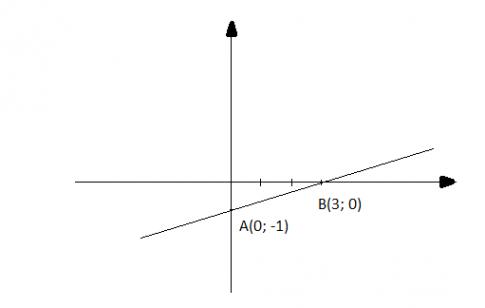
d) \(y = \frac{1}{3}x - 1\)
Cho x = 0 thì y = - 1, ta được điểm A(0; -1)
Cho y = 0 thì x = 3, ta được điểm B(3; 0)
Câu 4: Trang 38 sách VNEN 9 tập 1
Không vẽ đồ thị hàm số: y = 1,5x + 10, hãy cho biết trong các điểm sau, điểm nào thuộc đồ thị hàm số đã cho?
A(10; 25); B(-2; 7); C(4; - 4); D(0; 10).
Bài làm:
Ta thay các điểm vào hàm số y = 1,5x + 10, điểm nào thỏa mãn thì điểm đó thuộc đồ thị hàm số
A(10; 25): 25 = 1,5.10 + 10 suy ra A thuộc đồ thị
B(-2; 7): 7 = 1,5.(-2) + 10 suy ra B thuộc đồ thị
C(4; -4): -4 ≠ 1,5.4 + 10 suy ra C không thuộc đồ thị
D(0; 10): 10 = 1,5.0 + 10 suy ra D thuộc đồ thị
Vậy A(10; 25); B(-2; 7); D(0; 10) thuộc đồ thị hàm số.
Câu 5: Trang 38 sách VNEN 9 tập 1
Vẽ đồ thị của các hàm số:
a) y = -2; b) y = 1; c) y = 2,5; d) y = -1,5.
Bài làm:
a) y = -2
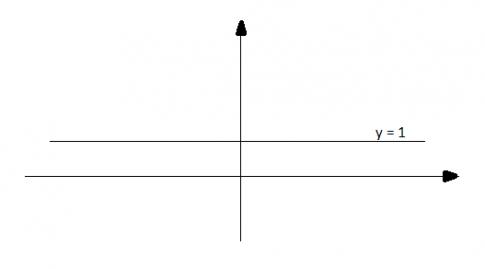
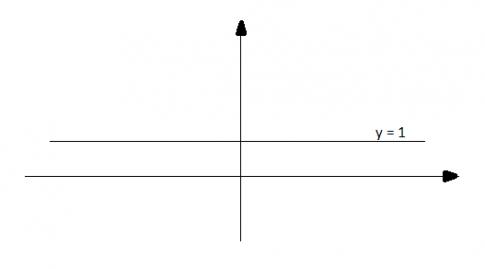
b) y = 1
c) y = 2,5
d) y = -1,5
Câu 6: Trang 38 sách VNEN 9 tập 1
Một cái can có dung tích 45l khi không chứa chất lỏng thì cân nặng 5kg, khối lượng của mỗi lít chất lỏng là 0,9kg. Hỏi rằng khi chứa p lít chất lỏng thì khối lượng cái can này là bao nhiêu ki-lô-gam?
Bài làm:
Gọi khối lượng của cái can là t (kg)
Can có dung tích 45l và khối lượng khi không chứa chất lỏng của can là 5kg
Ta có: t = 0,9.p + 5
Vậy khi chứa p lít chất lỏng thì khối lượng cái can này là t = 0,9.p + 5 (kg).
D. HOẠT ĐỘNG VẬN DỤNG
Câu 1: Trang 38 sách VNEN 9 tập 1
Cho hàm số bậc nhất y = kx - 3. Tìm k, biết rằng đồ thị hàm số đi qua điểm A(-1; 0,5)
Bài làm:
Đồ thị hàm số y = kx - 3 đi qua điểm A(-1; 0,5) tức là:
\(0,5 = k.(-1) - 3 \Leftrightarrow k = - 3,5\)
Vậy k = - 3,5.
Câu 2: Trang 38 sách VNEN 9 tập 1
Với giá trị nào của a thì điểm A (a; 2a - 1) thuộc đồ thị hàm số:
a) y = -2x + 3; b) y = -x + 5; c) f(x) = 3x - 1; d) \(f(x) = \frac{1}{3}x - \frac{2}{3}\)
Bài làm:
Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì điểm A phải thỏa mãn hàm số
a) Ta có: y = -2x + 3 = -2.a + 3 = -2a + 3. Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì \(2a - 1 = -2a + 3 \Leftrightarrow a = 1\)
b) Ta có: y = -x + 5 = -a + 5. Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì \(2a - 1 = -a + 5 \Leftrightarrow a = 2\)
c) Ta có: f(x) = 3x - 1 = 3a - 1. Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì \(2a - 1 = 3a - 1 \Leftrightarrow a = 0\)
d) Ta có: \(f(x) = \frac{1}{3}x - \frac{2}{3} = \frac{1}{3}a - \frac{2}{3}\). Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì \(2a - 1 = \frac{1}{3}x - \frac{2}{3} \Leftrightarrow a = \frac{1}{5}.\)
Câu 3: Trang 38 sách VNEN 9 tập 1
Một thanh sắt ở nhiệt độ \(t = 0^{\circ}C\) có chiều dài là l = 10m. Khi nhiệt độ thay đổi thì chiều dài thanh sắt dãn nở theo công thức \(l = 10(1 + 0,000012t)\), trong đó \(-100^{\circ} < t < 200^{\circ}\). Hãy cho biết:
a) Độ dài thanh sắt khi t bằng \(0^{\circ}C; 50^{\circ}C; -50^{\circ}C\)
b) Thanh sắt dài thêm bao nhiêu mi-li-mét nếu nhiệt độ tăng từ \(-20^{\circ}C\) đến \(80^{\circ}C\).
Bài làm:
a) Khi t bằng \(0^{\circ}C\) thì độ dài thanh sắt là \(l = 10(1 + 0,000012t) = 10(1 + 0,000012.0) = 10^{\circ}C\)
Khi t bằng \(50^{\circ}C\) thì độ dài thanh sắt là \(l = 10(1 + 0,000012t) = 10(1 + 0,000012.50) = 10,006^{\circ}C\)
Khi t bằng \(- 50^{\circ}C\) thì độ dài thanh sắt là \(l = 10(1 + 0,000012t) = 10(1 + 0,000012.(- 50)) = 9,994^{\circ}C\)
b) Khi t bằng \(- 20^{\circ}C\) thì độ dài thanh sắt là \(l1 = 10(1 + 0,000012t) = 10(1 + 0,000012.(- 20)) = 9,9976^{\circ}C\)
Khi t bằng \(80^{\circ}C\) thì độ dài thanh sắt là \(l2 = 10(1 + 0,000012t) = 10(1 + 0,000012.80) = 10,0096^{\circ}C\)
Suy ra khi nhiệt độ tăng từ \(-20^{\circ}C\) đến \(80^{\circ}C\) thì độ dài thanh sắt tăng thêm là \(l'=l2-l1=10,0096-9,9976=0,012^oC.\)
Câu 4: Trang 38 sách VNEN 9 tập 1
Đồ thị của hàm số \(y = \sqrt{3}x + \sqrt{3}\) được vẽ bằng compa bà thước thẳng như hình 3.
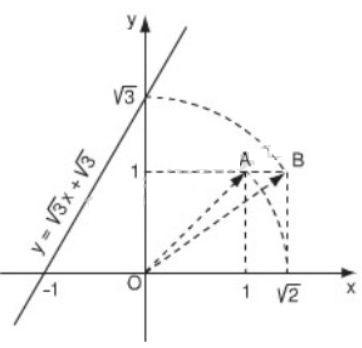
Hãy tìm hiểu cách vẽ đó rồi nêu lại cách thực hiện.
Áp dung:
Vẽ đồ thị của hàm số \(y = \sqrt{5}x + \sqrt{5}\) bằng compa và thước thẳng.
Bài làm:
a)
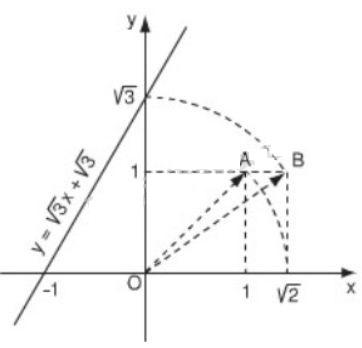
Vẽ đồ thị hàm số \(y = \sqrt{3}x + \sqrt{3}\)
Cho x = 0 thì \(y = \sqrt{3} \Leftrightarrow M(0; \sqrt{3})\)
Cho y = 0 thì \(x = - 1 \Leftrightarrow N(- 1; 0)\)
Đồ thị hàm số \(y = \sqrt{3}x + \sqrt{3}\) là đường thẳng đi qua hai điểm \(M(0; \sqrt{3})\) và \(N(- 1; 0)\)
Ta xác định vị trí của \(M(0; \sqrt{3})\) trên trục tung;
Bước 1: Xác định vị trí A(1; 1) trên mặt phẳng tọa độ Oxy, theo định lí Py-ta-go ta có: \(OA^{2} = 1^{2} + 1^{2} = 2 \Leftrightarrow OA = \sqrt{2}\)
Bước 2: Dùng compa vẽ cung tròn tâm O bán kính \(OA = \sqrt{2}\) cắt Ox tại C thì hoành độ của C là \(\sqrt{2}\).
Bước 3: Xác định điểm \(B(\sqrt{2}; 1)\). Theo định lí Py-ta=go ta có: \(OB^{2} = (\sqrt{2})^{2} + 1^{2} = 3\)
Bước 4: Dùng compa vẽ cung tròn tâm O bán kính \(OB = \sqrt{3}\) cắt Oy tại \(\sqrt{3}\) ta được \(M(0; \sqrt{3})\)
Bước 5: Kẻ đường thẳng đi qua hai điểm N và N ta được đồ thị hàm số \(y = \sqrt{3}x + \sqrt{3}\)
b)
Tương tự như cách làm câu a, ta được đồ thị của hàm số \(y = \sqrt{5}x + \sqrt{5}:\)
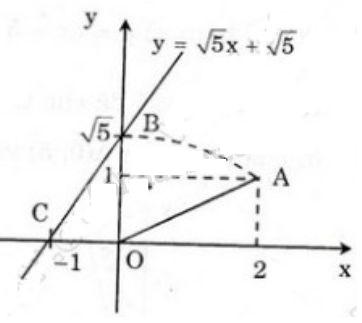
Soạn Toán 9 bài 1 Hàm số bậc nhất và đồ thị VNEN. Phần trên VnDoc đã hướng dẫn các bạn soạn Toán 9, trả lời các câu hỏi với lời giải chi tiết giúp các bạn nắm chắc kiến thức từ đó vận dụng tốt giải các bài tập Toán lớp 9. Chúc các bạn học tốt
.............................................
Ngoài Soạn Toán 9 bài 1 Hàm số bậc nhất và đồ thị VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt
