Soạn Toán 9 VNEN bài 1 Sự xác định đường tròn. Tính chất đối xứng của đường tròn VNEN được VnDoc sưu tầm và đăng tải, hy vọng sẽ giúp ích cho học tốt môn toán lớp 9, rút ngắn thời gian làm bài và soạn bài. Mời các bạn tải về tham khảo chuẩn bị tốt cho bài giảng sắp tới
- Đường tròn tâm O bán kính R (R > 0) là hình gồm.........
- Hình tròn là hình bao gồm các điểm nằm.........và nằm.......đường tròn.
- Hai điểm C,D bất kì thuộc đường tròn (O) chia đường tròn này thành hai phần, mỗi phần gọi là một........(hay còn gọi tắt là......). Hai điểm........gọi là hai mút của........
- Đoạn nối hai mút của cung gọi là.......(còn gọi tắt là......).
- Dây đi qua tâm là......của đường tròn.
Trả lời:
- Đường tròn tâm O bán kính R (R > 0) là hình gồm các điểm cách O một khoảng bằng R kí hiệu (O; R)
- Hình tròn là hình bao gồm các điểm nằm trong và nằm trên đường tròn.
- Hai điểm C,D bất kì thuộc đường tròn (O) chia đường tròn này thành hai phần, mỗi phần gọi là một cung tròn (hay còn gọi tắt là cung). Hai điểm C, D gọi là hai mút của cung.
- Đoạn nối hai mút của cung gọi là dây cung (còn gọi tắt là dây).
- Dây đi qua tâm là đường kính của đường tròn.
2. Điền vào chỗ chấm (...) (h.66)
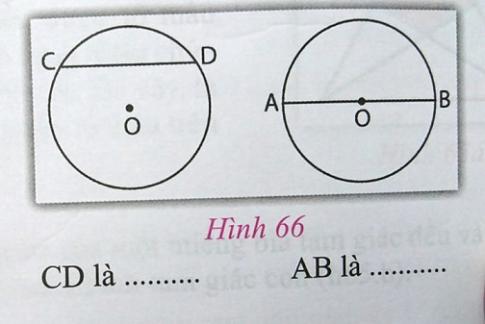
Trả lời:
- CD là dây cung
- AB là đường kính.
3. Quan sát hình vẽ và điền vào chỗ chấm (...)
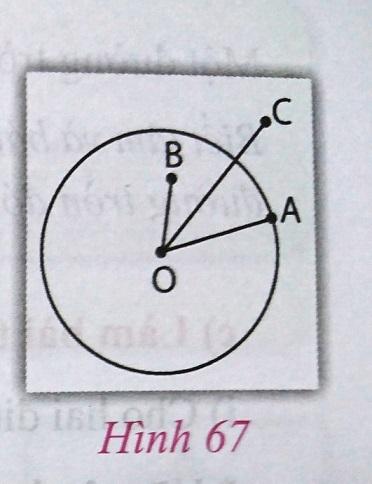
Cho đường tròn tâm O, bán kính R (h.67).
Vị trí của điểm với đường tròn | Hệ thức liên hệ |
Điểm A nằm trên đường tròn (O) (Điểm A thuộc đường tròn hay đường tròn (O) đi qua A). | OA……..R |
Điểm B nằm trong đường tròn (O; R) | OB………R |
Điểm C nằm ngoài (O; R) | OC………R |
Trả lời:
Vị trí của điểm với đường tròn | Hệ thức liên hệ |
Điểm A nằm trên đường tròn (O) (Điểm A thuộc đường tròn hay đường tròn (O) đi qua A). | OA = R |
Điểm B nằm trong đường tròn (O; R) | OB < R |
Điểm C nằm ngoài (O; R) | OC > R |
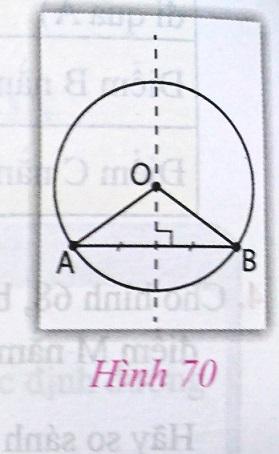
4. Cho hình 68, biết điểm N nằm trong đường tròn (O), điểm M nằm ngoài đường tròn (O).
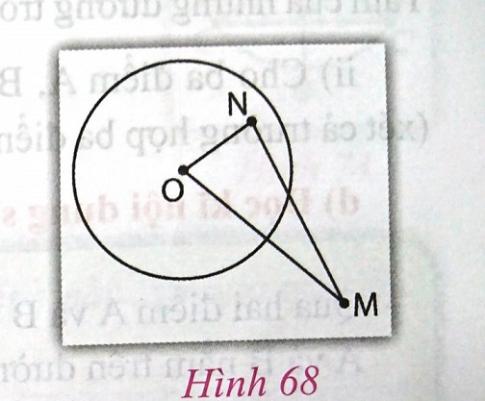
Hãy so sánh 
\(\widehat{OMN}\) và \(\widehat{ONM}\).
Trả lời:
Vì N nằm trong đường tròn (O) nên ON < R
Vì điểm M nằm ngoài đường tròn (O) nên OM > R
\(\Rightarrow OM > ON\)
Theo quan hệ giữa cạnh và góc trong tam giác OMN:
\(\widehat{OMN}\) đối diện với ON và \(\widehat{ONM}\) đối diện với OM nên \(\widehat{OMN} < \widehat{ONM}\).
a) Vẽ tiếp hình 69 theo yêu cầu sau:
- Vẽ đường tròn tâm A, bán kính 2cm.
- Cho đoạn thẳng CD = 3cm. Vẽ đường thẳng tâm O đường kính CD.
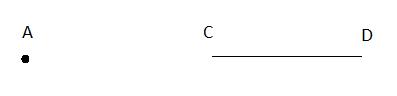
Trả lời:
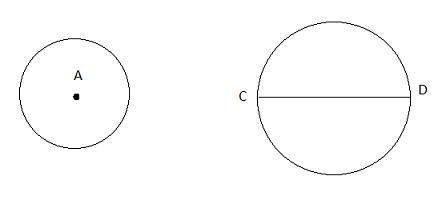
c) Làm bài tập sau:
i) Cho hai điểm A và B
* Vẽ một đường tròn đi qua hai điểm A và B.
* Có thể vẽ được bao nhiêu đường tròn đi qua hai điểm A và B? Tâm của những đường tròn đó nằm trên đường nào? Giải thích (h.70).
ii) Cho ba điểm A, B, C. Hãy vẽ đường tròn đi qua ba điểm đó (xét cả trường hợp ba điểm A, B, C thẳng hàng và không thẳng hàng).
Trả lời:
i)
* Qua hai điểm A và B có thể vẽ được vô số đường tròn. Tâm của nhưng đường tròn đó nằm trên đường trung trực của đoạn thẳng AB.
Vì A, B thuộc đường tròn nên OA = OB, hay O nằm trên đường trung trực của đoạn thẳng AB.
ii) * Qua ba điểm A, B, C không thẳng hàng chỉ vẽ được một đường tròn
* Qua ba điểm A, B, C thẳng hàng không vẽ được đường tròn.
2. Thực hiện các hoạt động sau
a) Giải các bài toán sau:
- Cho đường tròn tâm O, A là điểm bất kì thuộc đường tròn. Vẽ A' đối xứng với A qua O (h.73). Chứng minh rằng điểm A' cũng thuộc đường tròn tâm O.
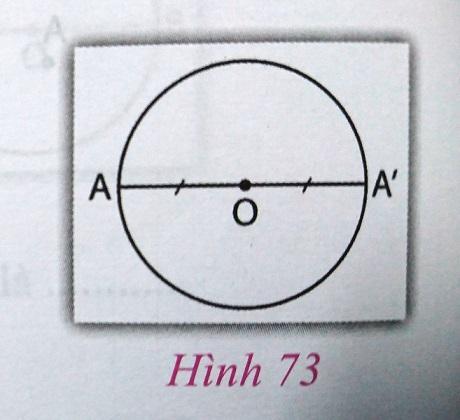
Trả lời:
A' đối xứng với A qua O nên OA' = OA = R
Vậy A' cũng thuộc đường tròn tâm O.
c) Giải bài toán sau:
Cho đường tròn (O), AB là một đường kính bất kì và C là điểm thuộc đường tròn. Vẽ C' đối xứng với C qua AB (h.74). Chứng minh rằng điểm C' cũng thuộc đường tròn (O).
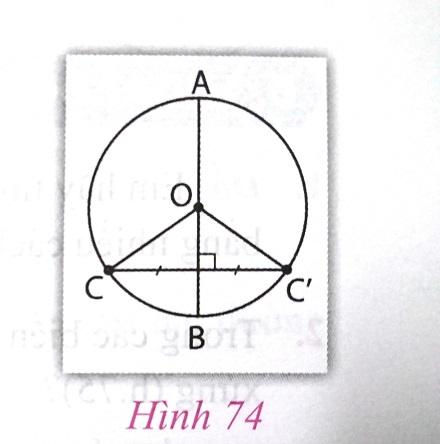
Trả lời:
AB là đường kính của đường tròn (O) nên O thuộc AB
Vì C' đối xứng với C qua AB nên OC' = OC = R hay C' cũng thuộc đường tròn (O).
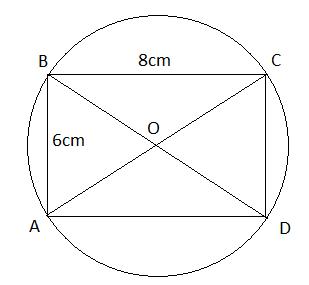
Cho hình chữ nhật ABCD có AB = 6cm, BC = 8cm. Chứng minh rằng 4 điểm A, B, C, D thuộc cùng một đường tròn, tìm tâm và tính bán kính của đường tròn đó.
Gọi O là giao điểm của hai đường chéo AC và BD
Ta có: OA = OB = OC = OD hay A, B, C, D thuộc cùng một đường tròn
Tâm của đường tròn là O
Bán kính của đường tròn là \(OA = OB = OC = OD = \frac{1}{2}BD = \frac{1}{2}\sqrt{AB^{2} + BC^{2}} = 5 cm.\)
Chứng minh các định lý sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuông.
a) Chứng minh: Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
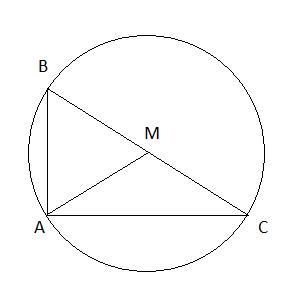
Gọi M là trung điểm của cạnh huyền BC
Theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông ta có: \(MA = MB = MC \Rightarrow A, B, C\) cùng thuộc một đường tròn tâm M hay âm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền (đpcm)
b) Chứng minh: Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuông
Giả sử tam giác ABC có BC là đường kính của đường tròn ngoại tiếp tam giác
Gọi M là trung điểm của BC suy ra M là tâm của đường tròn
Khi đó MA = MB = MC hay tam giác ABC vuông tại A
Vậy nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuông (đpcm).
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của các điểm \(A(1; 1), B(1; 2)\) và \(C(- \sqrt{2}; - \sqrt{2})\) đối với đường tròn tâm O bán kính là 2.
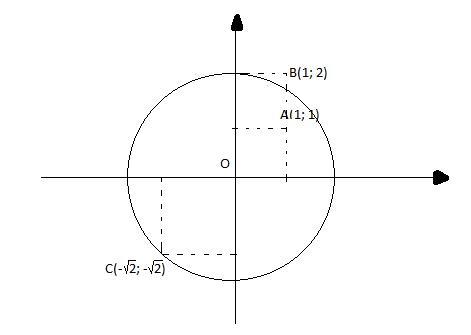
Ta có:
A nằm trong đường tròn (O),
B nằm ngoài đường tròn (O),
C nằm trên đường tròn (O).
Điền vào chỗ chấm (...)
a) Nếu tam giác có ba góc nhọn thì tâm đường tròn ngoại tiếp tam giác đó nằm bên.......................tam giác.
b) Nếu tam giác vuông thì tâm đường tròn ngoại tiếp tam giác đó là ......................................
c) Nếu tam giác có góc...........................thì tâm đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác.
a) Nếu tam giác có ba góc nhọn thì tâm đường tròn ngoại tiếp tam giác đó nằm bên trong tam giác.
b) Nếu tam giác vuông thì tâm đường tròn ngoại tiếp tam giác đó là trung điểm cạnh huyền
c) Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác.
Đố: Em hãy tìm tâm của các đĩa hình tròn bằng các kiến thức đã học (có thể tìm bằng nhiều cách).
Lấy ba điểm A, B, C bất kì thuộc đường tròn, ta được tam giác ABC nội tiếp đường tròn đó
Lấy giao điểm của ba đường trung trực của ba cạnh tam giác ta được tâm của đường tròn đó.
Trong các biển báo giao thông sau, biển nào có tâm đối xứng, biển nào có trục đối xứng (h.75)?
Biển có tâm đối xứng là biển cấm đi ngược chiều.
Biển có trục đối xứng là biển cấm ô tô.
Đố: Em hãy tìm hiểu thêm về dụng cụ tìm tâm của đường tròn
* Tìm tâm đường tròn bằng thước thẳng và com-pa
- Trên đường tròn lấy ba điểm A, B, C
- Vẽ dây AB và AC
-Dựng đường trung trực của AB, AC, chúng cắt nhau tại O thì O là tâm của đường tròn đó.
* Tìm tâm đường tròn bằng thước hình chữ T
Giả sử một thanh gỗ hình chữ T có hai đinh A, B và mép đường CD là trung trực của AB
Đặt mép của nắp hộp chạm vào A và B rồi vạch theo CD ta được đường thẳng đi qua tâm của nắp hộp. Xoay nắp hộp và làm tương tự, ta được đường thẳng khác đi qua tâm của nắp hộp. Giao điểm của hai đường thẳng vừa kẻ là tâm của nắp hộp.
Tại sao nghệ sĩ xiếc lại có thể đỡ được nhiều chiếc đĩa tròn trên đầu các thanh kim loại lâu như vậy (h.79)?
Giải thích:
Khi đầu que nâng đỡ trọng lực của đĩa, đĩa quay tròn theo trục là chiếc que, mỗi một điểm của bề mặt đĩa đều chuyển động vòng tròn. Do có quán tính, mỗi một điểm đều giữ trạng thái chuyên động vốn có, tức là chuyển động trên bề mặt phẳng của đĩa. Khi từng điểm một đều giữ được chuyển động trên mặt phẳng của đĩa ngay từ ban đầu, thì toàn bộ chiếc đĩa tự nhiên cũng sẽ chuyển động xoay theo que tre trên vị trí vốn có mà không bị rơi xuống. Chính vì vậy, cho dù người diễn viên kết hợp làm nhiều động tác cùng một lúc, nhưng chỉ cần người đó giữ vững phương hướng của những chiếc que thì những chiếc đĩa đang quay sẽ không bao giờ bị rơi xuống.
Giải bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn trang 88. Trên đây VnDoc đã hướng dẫn các bạn soạn Toán 9, lời giải chi tiết dễ hiểu hy vọng sẽ giúp các bạn củng cố thêm kiến thức từ đó vận dụng vào giải các các bài tập Toán lớp 9. Mời các bạn cùng tham khảo
.............................................
Ngoài Soạn Toán 9 bài 1 Sự xác định đường tròn. Tính chất đối xứng của đường tròn VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt
Lớp 9 
Soạn Toán 9 VNEN 
Đề thi học kì 2 lớp 9 
Toán 9 - Giải Toán lớp 9 Sách mới Hay nhất 
Văn mẫu lớp 9 Sách mới 
Bài tập Tiếng Anh lớp 9 
Vật lý lớp 9 
Hóa 9 - Giải Hoá 9 
Trắc nghiệm Văn 9 Sách mới 
Soạn Văn 9 Sách mới Giải Hoá 9 - Giải bài tập Hóa 9 Đề kiểm tra 15 phút lớp 9 
Sinh học lớp 9 
Lịch sử lớp 9 
Địa lý lớp 9 
