Hàm số bậc nhất là hàm số có dạng ![]() \(y = ax + b (a \neq 0)\)
\(y = ax + b (a \neq 0)\)
Vậy hàm số ![]() \(C. y= - \frac{8}{x}\) không phải là hàm số bậc nhất.
\(C. y= - \frac{8}{x}\) không phải là hàm số bậc nhất.
VnDoc xin giới thiệu tới các bạn bài Soạn Toán 9 VNEN bài 5 Ôn tập chương II, hy vọng với tài liệu này các bạn học sinh sẽ học tốt môn Toán lớp 9, rèn luyện kĩ năng giải bài tập. Mời các bạn tải về tham khảo
Trong các bà 1, 2, 3, 4, 5, 6 hãy chọn phương án đúng
Hàm số nào sau đây không phải là hàm số bậc nhất?
A. ![]() \(y = 5x + \sqrt{5}\); B.
\(y = 5x + \sqrt{5}\); B. ![]() \(y = (\sqrt{3} - 1)^{2}x + 1\);
\(y = (\sqrt{3} - 1)^{2}x + 1\);
C. ![]() \(y = - \frac{8}{x}\); D.
\(y = - \frac{8}{x}\); D. ![]() \(y = \sqrt{2}x - \sqrt{2}.\)
\(y = \sqrt{2}x - \sqrt{2}.\)
Hàm số bậc nhất là hàm số có dạng ![]() \(y = ax + b (a \neq 0)\)
\(y = ax + b (a \neq 0)\)
Vậy hàm số ![]() \(C. y= - \frac{8}{x}\) không phải là hàm số bậc nhất.
\(C. y= - \frac{8}{x}\) không phải là hàm số bậc nhất.
Hàm số nào sau đây là hàm số nghịch biến?
A. ![]() \(y = - 5 + 2x\); B.
\(y = - 5 + 2x\); B. ![]() \(y = 5 - 2x\);
\(y = 5 - 2x\);
C. ![]() \(y = (\sqrt{5} - 2)x - 9\); D.
\(y = (\sqrt{5} - 2)x - 9\); D. ![]() \(y = \sqrt{2}x - \sqrt{2}\).
\(y = \sqrt{2}x - \sqrt{2}\).
Hàm số y = ax + b là hàm số nghịch biến khi a < 0
Vậy hàm số B. y = 5 - 2x là hàm số nghịch biến.
Hàm số f(x) = (1 - 3m)x - 7 đồng biến khi và chỉ khi
A. ![]() \(m > - \frac{1}{3}\) B.
\(m > - \frac{1}{3}\) B. ![]() \(m < - \frac{1}{3}\)
\(m < - \frac{1}{3}\)
C. ![]() \(m > \frac{1}{3}\) D.
\(m > \frac{1}{3}\) D. ![]() \(m < \frac{1}{3}\)
\(m < \frac{1}{3}\)
Hàm số ![]() \(f(x) = (1 - 3m)x - 7\) đồng biến khi và chỉ khi
\(f(x) = (1 - 3m)x - 7\) đồng biến khi và chỉ khi ![]() \(1 - 3m > 0 \Leftrightarrow m < \frac{1}{3}\)
\(1 - 3m > 0 \Leftrightarrow m < \frac{1}{3}\)
Vậy đáp án là D.
Đồ thị hàm số ![]() \(y = ax + 2\) đi qua điểm
\(y = ax + 2\) đi qua điểm ![]() \(\left ( -\frac{1}{3}; - \frac{1}{4} \right )\) có hệ số góc bằng
\(\left ( -\frac{1}{3}; - \frac{1}{4} \right )\) có hệ số góc bằng
A. ![]() \(\frac{27}{4}\); B.
\(\frac{27}{4}\); B. ![]() \(\frac{21}{4}\); C.
\(\frac{21}{4}\); C. ![]() \(- \frac{21}{4}\); D. -24
\(- \frac{21}{4}\); D. -24
Đồ thị hàm số y = ax + 2 đi qua điểm ![]() \(\left ( -\frac{1}{3}; - \frac{1}{4} \right )\) tức là:
\(\left ( -\frac{1}{3}; - \frac{1}{4} \right )\) tức là:
![]() \(- \frac{1}{4} = a.(- \frac{1}{3}) + 2 \Leftrightarrow a = \frac{27}{4}\)
\(- \frac{1}{4} = a.(- \frac{1}{3}) + 2 \Leftrightarrow a = \frac{27}{4}\)
Vậy đáp án là A.
Đồ thị hàm số ![]() \(y = ax - \frac{1}{2}\) cắt trục hoành tại điểm có hoành độ bằng
\(y = ax - \frac{1}{2}\) cắt trục hoành tại điểm có hoành độ bằng ![]() \(\frac{1}{3}\). Hệ số góc của đường thẳng đó bằng?
\(\frac{1}{3}\). Hệ số góc của đường thẳng đó bằng?
A. ![]() \(\frac{1}{6}\); B.
\(\frac{1}{6}\); B. ![]() \(\frac{2}{3}\); C.
\(\frac{2}{3}\); C. ![]() \(\frac{5}{6}\); D.
\(\frac{5}{6}\); D. ![]() \(\frac{3}{2}\)
\(\frac{3}{2}\)
Đồ thị hàm số ![]() \(y = ax - \frac{1}{2}\) cắt trục hoành tại điểm có hoành độ bằng
\(y = ax - \frac{1}{2}\) cắt trục hoành tại điểm có hoành độ bằng ![]() \(\frac{1}{3}\), tức là đồ thị hàm số đi qua điểm
\(\frac{1}{3}\), tức là đồ thị hàm số đi qua điểm ![]() \((\frac{1}{3}; 0)\)
\((\frac{1}{3}; 0)\)
Khi đó, ta có: ![]() \(0 = a.\frac{1}{3} - \frac{1}{2} \Leftrightarrow a = \frac{3}{2}\)
\(0 = a.\frac{1}{3} - \frac{1}{2} \Leftrightarrow a = \frac{3}{2}\)
Vậy đáp án là D.
Nếu đường thẳng y = kx - 2 đi qua điểm (-1; 5) thì hệ số góc của nó bằng:
A. 10; B. - 7; C. - 3; D.1 9
Đường thẳng y = kx - 2 đi qua điểm (-1; 5) thì ta có: ![]() \(5 = k.(-1) - 2 \Leftrightarrow k = - 7\)
\(5 = k.(-1) - 2 \Leftrightarrow k = - 7\)
Suy ra hệ số góc của đường thẳng là k = - 7
Vậy đáp án là B.
Cho hàm số bậc nhất ![]() \(y = (m - 2)x + 4 (m \neq 2)\). Tìm giá trị của m để đồ thị hàm số:
\(y = (m - 2)x + 4 (m \neq 2)\). Tìm giá trị của m để đồ thị hàm số:
a) Đi qua điểm ![]() \((-1; 9)\);
\((-1; 9)\);
b) Cắt trục hoành tại điểm có hoành độ bằng 3;
c) Tạo với tia Ox góc ![]() \(135^{\circ}\)
\(135^{\circ}\)
Cho hàm số bậc nhất ![]() \(y = (m - 2)x + 4 (m \neq 2)\). Tìm giá trị của m để đồ thị hàm số:
\(y = (m - 2)x + 4 (m \neq 2)\). Tìm giá trị của m để đồ thị hàm số:
a) Hàm số ![]() \(y = (m - 2)x + 4 (m \neq 2)\) đi qua điểm
\(y = (m - 2)x + 4 (m \neq 2)\) đi qua điểm ![]() \((-1; 9)\) thì ta có:
\((-1; 9)\) thì ta có: ![]() \(9 = (m - 2).(-1) + 4 \Leftrightarrow m = - 3\)
\(9 = (m - 2).(-1) + 4 \Leftrightarrow m = - 3\)
Vậy m = 3
b) Hàm số ![]() \(y = (m - 2)x + 4 (m \neq 2)\) cắt trục hoành tại điểm có hoành độ bằng 3 tức là hàm số đi qua điểm (3 ; 0)
\(y = (m - 2)x + 4 (m \neq 2)\) cắt trục hoành tại điểm có hoành độ bằng 3 tức là hàm số đi qua điểm (3 ; 0)
Ta có: ![]() \(0 = (m - 2).3 + 4 \Leftrightarrow m = \frac{2}{3}\)
\(0 = (m - 2).3 + 4 \Leftrightarrow m = \frac{2}{3}\)
Vậy ![]() \(m = \frac{2}{3}\).
\(m = \frac{2}{3}\).
c) Ta có hình sau:
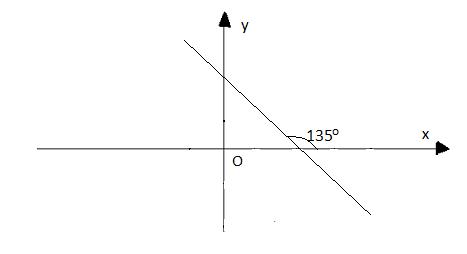
Gọi giao điểm của đồ thị hàm số ![]() \(y = (m - 2)x + 4 (m \neq 2)\) với trục hoành là A, với trục tung là B
\(y = (m - 2)x + 4 (m \neq 2)\) với trục hoành là A, với trục tung là B
Ta có tọa độ của A, B lần lượt là ![]() \(A(\frac{4}{2 - m} ; 0)\),
\(A(\frac{4}{2 - m} ; 0)\), ![]() \(B(0; 4)\)
\(B(0; 4)\)
Vì đồ thị hàm số tạo với Ox góc ![]() \(135^{\circ}\) nên
\(135^{\circ}\) nên ![]() \(\widehat{BAO} = 45^{\circ}\)
\(\widehat{BAO} = 45^{\circ}\)
Suy ra ![]() \(\frac{4}{2 - m} = 4 \Leftrightarrow m = 1\)
\(\frac{4}{2 - m} = 4 \Leftrightarrow m = 1\)
Vậy m = 1.
Cho các đường thẳng
y = 3x - 1 (d1); y = ![]() \(- \frac{2}{3}x + 5 (d2)\); y = 3x - 4 (d3).
\(- \frac{2}{3}x + 5 (d2)\); y = 3x - 4 (d3).
Không vẽ các đường thẳng trên, hãy cho biết các đường thẳng đó có vị trí như thế nào với nhau.
Đường thẳng (d1) và (d2) có hệ số góc bằng nhau và ![]() \(- 1 \neq 4\) nên
\(- 1 \neq 4\) nên ![]() \((d1) // (d2)\).
\((d1) // (d2)\).
Đường thẳng (d1) và (d3) có hệ số góc khác nhau nên cắt nhau
Đường thẳng (d2) và (d3) có hệ số góc khác nhau nên cắt nhau.
Cho hai đường thẳng ![]() \(y = 2x + 4 (d1)\);
\(y = 2x + 4 (d1)\); ![]() \(y = - \frac{1}{2}x + 1 (d2)\)
\(y = - \frac{1}{2}x + 1 (d2)\)
(d1) cắt Ox tại A, cắt Oy tại B;
(d2) cắt Ox tại C, cắt Oy tại D;
(d1) cắt (d2) tại M.
a) Chứng minh MAC vuông tại M.
b) Tính diện tích tam giác MAC.
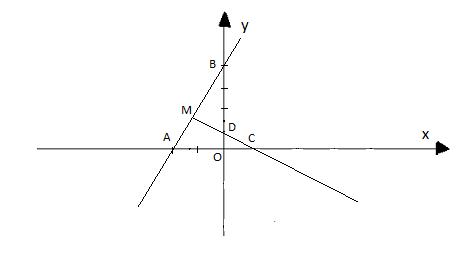
a) Đường thẳng ![]() \(y = 2x + 4 (d1)\) và
\(y = 2x + 4 (d1)\) và ![]() \(y = - \frac{1}{2}x + 1 (d2)\) có hệ số góc
\(y = - \frac{1}{2}x + 1 (d2)\) có hệ số góc ![]() \(a1.a2 = 2.(- \frac{1}{2}) = -1\) nên
\(a1.a2 = 2.(- \frac{1}{2}) = -1\) nên ![]() \((d1) \perp (d2)\) hay
\((d1) \perp (d2)\) hay ![]() \(MA \perp MC\) hay tam giác
\(MA \perp MC\) hay tam giác
MAC vuông tại M.
b) Ta có: AC = 2 + 2 = 4
![]() \(DC = \sqrt{OD^{2} + OC^{2}} = \sqrt{1^{2} + 2^{2}} = \sqrt{5}\)
\(DC = \sqrt{OD^{2} + OC^{2}} = \sqrt{1^{2} + 2^{2}} = \sqrt{5}\)
Ta có:  \(Sin\widehat{OCD} = \frac{OD}{DC} = \frac{1}{\sqrt{5}}\)
\(Sin\widehat{OCD} = \frac{OD}{DC} = \frac{1}{\sqrt{5}}\)
Ta có:  \(Sin\widehat{MCA} = \frac{MA}{AC} \Leftrightarrow \frac{1}{\sqrt{5}} = \frac{MA}{4} \Leftrightarrow MA = \frac{4}{\sqrt{5}}\)
\(Sin\widehat{MCA} = \frac{MA}{AC} \Leftrightarrow \frac{1}{\sqrt{5}} = \frac{MA}{4} \Leftrightarrow MA = \frac{4}{\sqrt{5}}\)
Áp dụng định lí Py-ta-go ta có: ![]() \(MC = \sqrt{AC^{2} - MA^{2}} = \frac{8}{\sqrt{5}}.\)
\(MC = \sqrt{AC^{2} - MA^{2}} = \frac{8}{\sqrt{5}}.\)
Diện tích tam giác MAC là ![]() \(S\Delta MAC = \frac{1}{2}.MA.MC = \frac{16}{5}.\)
\(S\Delta MAC = \frac{1}{2}.MA.MC = \frac{16}{5}.\)
Xác định hàm số y = ax + b, biết rằng đồ thị của nó cắt trục hoành tại điểm có hoành độ bằng 3 và tạo với tia Ox góc ![]() \(45^{\circ}\).
\(45^{\circ}\).
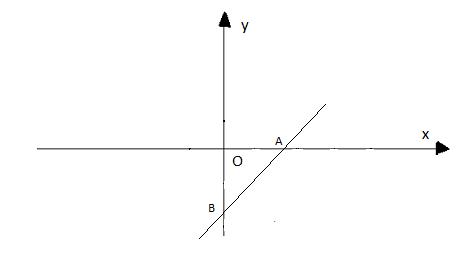
Giả sử hàm số y = ax + b cắt Ox, Oy lần lượt tại hai điểm A, B
Theo bài ra hàm số y = ax + b cắt trục hoành tại điểm có hoành độ bằng 3 nên A có tọa độ là A(3; 0)
Vì hàm số tạo với Ox góc ![]() \(45^{\circ}\) nên OB = OA, theo hình vẽ ta được B có tọa độ B(0; - 3)
\(45^{\circ}\) nên OB = OA, theo hình vẽ ta được B có tọa độ B(0; - 3)
Hàm số y = ax + b đi qua hai điểm A(3; 0) và B(0; - 3) nên ta có hàm số y = x - 3
Vậy hàm số cần tìm là y = x - 3.
Cho hàm số ![]() \(y = mx - 2 (m \neq 0)\).
\(y = mx - 2 (m \neq 0)\).
a) Với giá trị nào của m thì hàm số đồng biến? Nghịch biến?
b) Xác định giá trị của m để đồ thị hàm số đi qua điểm A(1; 2). Vẽ đồ thị ứng với giá trị m tìm được.
c) Chứng minh rằng với mọi giá trị của m, đồ thị hàm số đã cho đi qua một điểm cố định.
d) Xác định giá trị của m để đồ thị hàm số cắt hai trục tọa độ thành tam giác diện tích bằng 1.
a) Hàm số y = mx - 2 đồng biến khi m > 0, nghịch biến khi m < 0.
b) Đồ thị hàm số y = mx - 2 đi qua điểm A(1; 2) thì ![]() \(2 = m.1 - 2 \Leftrightarrow m = 4\)
\(2 = m.1 - 2 \Leftrightarrow m = 4\)
Vậy hàm số là y = 4x - 2
Ta có đồ thị như sau:
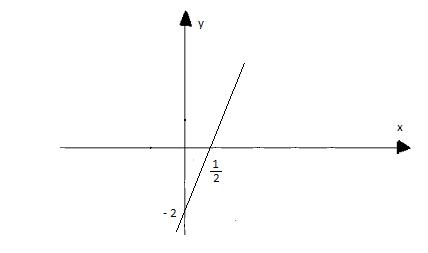
c) Gọi điểm cố định mà hàm số đi qua là ![]() \(M(x0; y0)\)
\(M(x0; y0)\)
Ta có phương trình hoành độ giao điểm là ![]() \(y0 = mx0 - 2 \Leftrightarrow mx0 - (2 + y0) = 0\)
\(y0 = mx0 - 2 \Leftrightarrow mx0 - (2 + y0) = 0\)
Vì phương trình có nghiệm với mọi giá trị của m nên
x0 = 0 và ![]() \(2 + y0 = 0 \Leftrightarrow x0 = 0\) và y0 = - 2
\(2 + y0 = 0 \Leftrightarrow x0 = 0\) và y0 = - 2
Vạy hàm số luôn đi qua điểm cố định M(0; -2).
d) Giả sử hàm số cắt trục hoành, trục tung lần lượt tại A, B
Ta có tọa độ của A, B là ![]() \(A(\frac{2}{m}; 0); (0; -2)\)
\(A(\frac{2}{m}; 0); (0; -2)\)
Theo bài ra đồ thị hàm số cắt hai trục tọa độ thành tam giác diện tích bằng 1 hay:
![]() \(\frac{1}{2}.\left | \frac{2}{m} \right |.\left |- 2 \right | = 1\)
\(\frac{1}{2}.\left | \frac{2}{m} \right |.\left |- 2 \right | = 1\)
![]() \(\Leftrightarrow \left | \frac{2}{m} \right | = 1\)
\(\Leftrightarrow \left | \frac{2}{m} \right | = 1\)
![]() \(\Leftrightarrow m = 2\) hoặc m = - 2
\(\Leftrightarrow m = 2\) hoặc m = - 2
Vậy m = 2 hoặc m = -2.
Một bể nước có 200 lít nước. Người ta cho một vòi chảy vào bể, mỗi phút vòi chảy được 25 lít.
a) Sau x phút, lượng nước trong bể là y lít, lập hàm số biểu thị quan hệ giữa y và x.
b) Vẽ đồ thị của hàm số biết rằng dung tích của bể là 1200 lít.
a) Ban đầu bể nước có 200 lít nước, mỗi phút vòi chảy được 25 lít, sau x phút lượng nước trong bể là:
y = 25x + 200 (lít) (x > 0, y > 200)
b) Ta có biểu thức thể hiện dung tích của bể theo phút là:
y = 25x + 200 (lít) (x > 0, y > 200)
Dung tích của bể là 1200 lít tức là y = 1200 suy ra x = 40
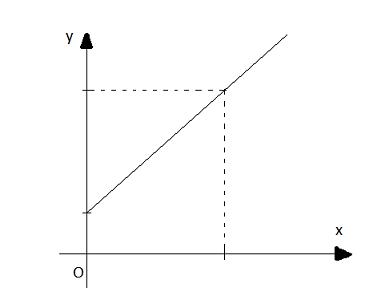
Vậy đồ thị hàm số đi qua hai điểm (40; 1200); (0; 200)
Giải bài 5: Ôn tập chương II - Sách VNEN toán 9 tập 1 trang 53. Phần trên VnDoc đã hướng dẫn các bạn soạn Toán 9, trả lời các câu hỏi với lời giải chi tiết giúp các bạn nắm chắc kiến thức từ đó vận dụng tốt giải các bài tập Toán lớp 9. Chúc các bạn học tốt
.............................................
Ngoài Soạn Toán 9 bài 5 Ôn tập chương II VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
 Lớp 9
Lớp 9
 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 lớp 9
Đề thi học kì 2 lớp 9
 Đề thi học kì 2 lớp 9 môn Vật Lý
Đề thi học kì 2 lớp 9 môn Vật Lý
 Đề thi học kì 2 lớp 9 môn Sinh Học
Đề thi học kì 2 lớp 9 môn Sinh Học
 Đề thi học kì 2 lớp 9 môn Địa
Đề thi học kì 2 lớp 9 môn Địa

