Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

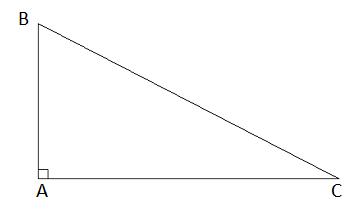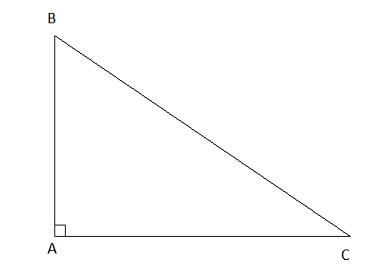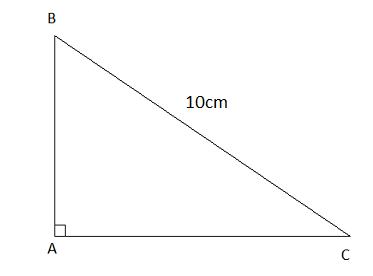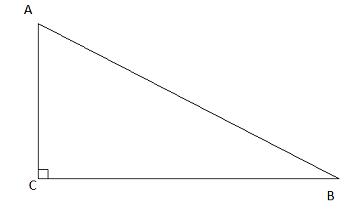
Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

Soạn Toán 9 tập 1 phần hình học

Bài trước

Bài sau

Soạn Toán 9 VNEN bài 3 Tỉ số lượng giác của góc nhọn. Đây là lời giải hay cho các câu hỏi trong Sách SGK nằm trong chương trình giảng dạy môn Toán lớp 9. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các bạn học sinh. Mời thầy cô cùng các bạn học sinh tham khảo

Bài 3 Tỉ số lượng giác của góc nhọn VNEN

B. Hoạt động hình thành kiến thức
- 2.a) Tìm hiểu mỗi quan hệ giữa tỉ số lượng giác của hai góc phụ nhau thông qua hoạt động sau
C. Hoạt động luyện tập
D.E. Hoạt động vận dụng và tìm tòi, mở rộng
- 1. Trang 69 sách VNEN 9 tập 1

B. Hoạt động hình thành kiến thức

1.b)

Điền vào chỗ trống để hoàn thành các công thức sau (h.32):

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

$sin\alpha = \frac{cạnh đối}{cạnh huyền} = \frac{AC}{BC};$ $sin\alpha = \frac{cạnh đối}{cạnh huyền} = \frac{AC}{BC};$

$cos\alpha = \frac{cạnh kề}{cạnh huyền} = \frac{.......}{.......};$ $cos\alpha = \frac{cạnh kề}{cạnh huyền} = \frac{.......}{.......};$

$tan\alpha = \frac{cạnh đối}{cạnh kề} = \frac{........}{........};$ $tan\alpha = \frac{cạnh đối}{cạnh kề} = \frac{........}{........};$

$cot\alpha = \frac{cạnh kề}{cạnh đối} = \frac{.........}{........}.$ $cot\alpha = \frac{cạnh kề}{cạnh đối} = \frac{.........}{........}.$

Trả lời:

$sin\alpha = \frac{cạnh đối}{cạnh huyền} = \frac{AC}{BC};$ $sin\alpha = \frac{cạnh đối}{cạnh huyền} = \frac{AC}{BC};$

$cos\alpha = \frac{cạnh kề}{cạnh huyền} = \frac{AB}{BC};$ $cos\alpha = \frac{cạnh kề}{cạnh huyền} = \frac{AB}{BC};$

$tan\alpha = \frac{cạnh đối}{cạnh kề} = \frac{AC}{AB};$ $tan\alpha = \frac{cạnh đối}{cạnh kề} = \frac{AC}{AB};$

$cot\alpha = \frac{cạnh kề}{cạnh đối} = \frac{AB}{AC}.$ $cot\alpha = \frac{cạnh kề}{cạnh đối} = \frac{AB}{AC}.$

c) Làm bài tập sau

Bài tập 1: Tính các tỉ số lượng giác của góc nhọn $\alpha$ $\alpha$trong hình 33 sau:

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

$sin\alpha = \frac{MN}{NP} = \frac{........}{.......}$ $sin\alpha = \frac{MN}{NP} = \frac{........}{.......}$

$cos\alpha = \frac{.......}{........} = \frac{........}{........}$ $cos\alpha = \frac{.......}{........} = \frac{........}{........}$

$tan\alpha = \frac{.......}{........} = \frac{........}{........}$ $tan\alpha = \frac{.......}{........} = \frac{........}{........}$

$cot\alpha = \frac{.......}{........} = \frac{........}{........}$ $cot\alpha = \frac{.......}{........} = \frac{........}{........}$

Trả lời:

$sin\alpha = \frac{MN}{NP} = \frac{6}{10}$ $sin\alpha = \frac{MN}{NP} = \frac{6}{10}$

$cos\alpha = \frac{MP}{NP} = \frac{8}{10}$ $cos\alpha = \frac{MP}{NP} = \frac{8}{10}$

$tan\alpha = \frac{MN}{MP} = \frac{6}{8}$ $tan\alpha = \frac{MN}{MP} = \frac{6}{8}$

$cot\alpha = \frac{MP}{MN} = \frac{8}{6}.$ $cot\alpha = \frac{MP}{MN} = \frac{8}{6}.$

2.a) Tìm hiểu mỗi quan hệ giữa tỉ số lượng giác của hai góc phụ nhau thông qua hoạt động sau

- Quan sát hình 33.

- Tính các tỉ số lượng giác của góc $\beta .$ $\beta .$

- Nhận xét mối quan hệ giữa $\alpha$ $\alpha$và $\beta$ $\beta$, $sin\alpha$ $sin\alpha$và $cos\beta$ $cos\beta$, $cos\alpha$ $cos\alpha$và $sin\beta$ $sin\beta$, $cot\alpha$ $cot\alpha$và $tan\beta, tan \alpha$ $tan\beta, tan \alpha$và $cot\beta.$ $cot\beta.$

Trả lời:

- Tính:

$sin\beta = \frac{MP}{NP} = \frac{8}{10}$ $sin\beta = \frac{MP}{NP} = \frac{8}{10}$

$cos\beta = \frac{MN}{NP} = \frac{6}{10}$ $cos\beta = \frac{MN}{NP} = \frac{6}{10}$

$tan\beta = \frac{MP}{MN} = \frac{8}{6}.$ $tan\beta = \frac{MP}{MN} = \frac{8}{6}.$

$cot\beta = \frac{MN}{MP} = \frac{6}{8}.$ $cot\beta = \frac{MN}{MP} = \frac{6}{8}.$

- Nhận xét:

$\alpha + \beta = 90^{\circ}$ $\alpha + \beta = 90^{\circ}$

$sin\alpha = cos\beta$ $sin\alpha = cos\beta$

$cos\alpha = sin\beta$ $cos\alpha = sin\beta$

$tan\alpha = cot\beta$ $tan\alpha = cot\beta$

$cot\alpha = tan\beta .$ $cot\alpha = tan\beta .$

c) Thực hiện hoạt động sau để tìm hiểu các tỉ số lượng giác của góc $30^{\circ}, 45^{\circ}, 60^{\circ}$ $30^{\circ}, 45^{\circ}, 60^{\circ}$

Bài tập 2 (h,35). Cho tam giác ABC vuông cân tại A, AB = 5cm. Điền tiếp vào chỗ chấm (....):

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

$AC = AB = ............(cm) ;$

$BC = \sqrt{AB^{2} + AC^{2}} = .............= ..............(cm).$ $BC = \sqrt{AB^{2} + AC^{2}} = .............= ..............(cm).$

Tam giác ABC vuông cân tại A nên $\widehat{ABC} = 45^{\circ} ;$ $\widehat{ABC} = 45^{\circ} ;$

$sin45^{\circ} = \frac{AC}{BC} = ...........; cos45^{\circ} = \frac{AC}{BC} = ...........;$ $sin45^{\circ} = \frac{AC}{BC} = ...........; cos45^{\circ} = \frac{AC}{BC} = ...........;$

$tan45^{\circ} = \frac{AC}{BC} = ...........; cot45^{\circ} = \frac{AC}{BC} = ...........;$ $tan45^{\circ} = \frac{AC}{BC} = ...........; cot45^{\circ} = \frac{AC}{BC} = ...........;$

Trả lời:

$AC = AB = 5 (cm) ;$

$BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{5^{2} + 5^{2}} = 5\sqrt{2}(cm).$ $BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{5^{2} + 5^{2}} = 5\sqrt{2}(cm).$

Tam giác ABC vuông cân tại A nên $\widehat{ABC} = 45^{\circ} ;$ $\widehat{ABC} = 45^{\circ} ;$

$sin45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}} ; cos45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}};$ $sin45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}} ; cos45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}};$

$tan45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}} ; cot45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}};$ $tan45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}} ; cot45^{\circ} = \frac{AC}{BC} = \frac{1}{\sqrt{2}};$

Bài tập 3 (h.36). Cho tam giác ABC đều cạnh 4cm, đường cao AH. Tính số đo độ dài các cạnh AB, AH, BH của tam giác ABH, từ đó tính tỉ số lượng giác của các góc $\alpha , \beta .$ $\alpha , \beta .$

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

Trả lời:

Gọi tên các góc như trong hình vẽ

Tam giác ABC đều nên $AB = AC = BC = 4cm và \widehat{ABC} = \widehat{BAC} = \widehat{ACB} = 60^{\circ}$ $AB = AC = BC = 4cm và \widehat{ABC} = \widehat{BAC} = \widehat{ACB} = 60^{\circ}$

$BH = \frac{1}{2}BC = \frac{1}{2}.4 = 2cm$ $BH = \frac{1}{2}BC = \frac{1}{2}.4 = 2cm$

Theo định lý Py-ta-go ta có: $AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{4^{2} - 2^{2}} = 2\sqrt{3}cm$ $AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{4^{2} - 2^{2}} = 2\sqrt{3}cm$

$* sin\alpha = \frac{BH}{AB} = \frac{2}{4} = \frac{1}{2}; cos\alpha = \frac{AH}{AB} = \frac{2\sqrt{3}}{4} = \frac{\sqrt{3}}{2}$ $* sin\alpha = \frac{BH}{AB} = \frac{2}{4} = \frac{1}{2}; cos\alpha = \frac{AH}{AB} = \frac{2\sqrt{3}}{4} = \frac{\sqrt{3}}{2}$

$tan\alpha = \frac{BH}{AH} = \frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}} ; cot\alpha = \frac{AH}{BH} = \frac{2\sqrt{3}}{2} = \sqrt{3}$ $tan\alpha = \frac{BH}{AH} = \frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}} ; cot\alpha = \frac{AH}{BH} = \frac{2\sqrt{3}}{2} = \sqrt{3}$

$* sin\beta = \frac{AH}{AB} = \frac{2\sqrt{3}}{4} = \frac{\sqrt{3}}{2} ; cos\beta = \frac{BH}{AB} = \frac{2}{4} = \frac{1}{2}$ $* sin\beta = \frac{AH}{AB} = \frac{2\sqrt{3}}{4} = \frac{\sqrt{3}}{2} ; cos\beta = \frac{BH}{AB} = \frac{2}{4} = \frac{1}{2}$

$tan\beta = \frac{AH}{BH} = \frac{2\sqrt{3}}{2} = \sqrt{3} ; cot\beta = \frac{BH}{AH} = \frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}}.$ $tan\beta = \frac{AH}{BH} = \frac{2\sqrt{3}}{2} = \sqrt{3} ; cot\beta = \frac{BH}{AH} = \frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}}.$

C. Hoạt động luyện tập

Câu 1: Trang 69 sách VNEN 9 tập 1

Cho tam giác ABC vuông tại C, AC = 0,9cm, BC = 1,2cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A

Bài làm:

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

Áp dụng định lý Py-ta-go trong tam giác ABC ta có:

$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{0,9{2} + 1,2^{2}} = 1,5cm$ $AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{0,9{2} + 1,2^{2}} = 1,5cm$

Ta có:

$sinB = \frac{AC}{AB} = \frac{0,9}{1,5} = \frac{3}{5}$ $sinB = \frac{AC}{AB} = \frac{0,9}{1,5} = \frac{3}{5}$

$cosB = \frac{BC}{AB} = \frac{1,2}{1,5} = \frac{4}{5}$ $cosB = \frac{BC}{AB} = \frac{1,2}{1,5} = \frac{4}{5}$

$tanB = \frac{AC}{BC} = \frac{0,9}{1,2} = \frac{3}{4}$ $tanB = \frac{AC}{BC} = \frac{0,9}{1,2} = \frac{3}{4}$

$cotB = \frac{BC}{AC} = \frac{1,2}{0,9} = \frac{4}{3}$ $cotB = \frac{BC}{AC} = \frac{1,2}{0,9} = \frac{4}{3}$

Ta có: $\widehat{A} + \widehat{B} = 90^{\circ}$ $\widehat{A} + \widehat{B} = 90^{\circ}$ nên:

$sin A = cosB = \frac{BC}{AB} = \frac{1,2}{1,5} = \frac{4}{5}$ $sin A = cosB = \frac{BC}{AB} = \frac{1,2}{1,5} = \frac{4}{5}$

$cos A = sinB = \frac{AC}{AB} = \frac{0,9}{1,5} = \frac{3}{5}$ $cos A = sinB = \frac{AC}{AB} = \frac{0,9}{1,5} = \frac{3}{5}$

$tan A = cotB = \frac{BC}{AC} = \frac{1,2}{0,9} = \frac{4}{3}$ $tan A = cotB = \frac{BC}{AC} = \frac{1,2}{0,9} = \frac{4}{3}$

$cot A = tanB = \frac{AC}{BC} = \frac{0,9}{1,2} = \frac{3}{4}.$ $cot A = tanB = \frac{AC}{BC} = \frac{0,9}{1,2} = \frac{3}{4}.$

Câu 2: Trang 69 sách VNEN 9 tập 1

Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn $45^{\circ}: sin60{\circ} ; cos63^{\circ} ; tan52^{\circ} ; cot81^{\circ}$ $45^{\circ}: sin60{\circ} ; cos63^{\circ} ; tan52^{\circ} ; cot81^{\circ}$

Bài làm:

Áp dụng tính chất: Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia

Do đó:

$\sin60^{\circ}=\cos30^{\circ}$ $\sin60^{\circ}=\cos30^{\circ}$

$cos63^{\circ} = sin27^{\circ}$ $cos63^{\circ} = sin27^{\circ}$

$tan52^{\circ} = cot38^{\circ}$ $tan52^{\circ} = cot38^{\circ}$

$cot81^{\circ} = tan9^{\circ}.$ $cot81^{\circ} = tan9^{\circ}.$

Câu 3: Trang 69 sách VNEN 9 tập 1

Vẽ tam giác ABC vuông tại $A, \widehat{B} = \alpha ,$ $A, \widehat{B} = \alpha ,$ biết:

a) $tan\alpha = 2$ $tan\alpha = 2$; b) $sin\alpha = \frac{3}{5}$ $sin\alpha = \frac{3}{5}$

Bài làm:

a) Ta có:

$tan\alpha = 2 \Leftrightarrow tanB = 2 \Leftrightarrow \frac{AC}{AB} = 2$ $tan\alpha = 2 \Leftrightarrow tanB = 2 \Leftrightarrow \frac{AC}{AB} = 2$

Ta được hình vẽ:

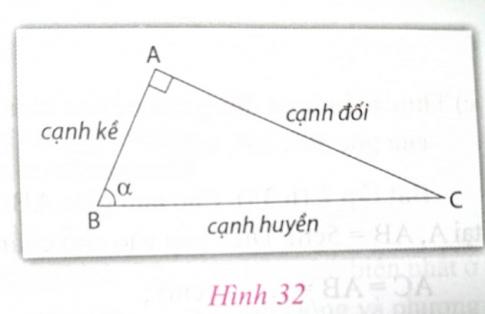
Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

b) Ta có;

$sin\alpha = \frac{3}{5} \Leftrightarrow sinB = \frac{3}{5} \Leftrightarrow \frac{AC}{BC} = \frac{3}{5}$ $sin\alpha = \frac{3}{5} \Leftrightarrow sinB = \frac{3}{5} \Leftrightarrow \frac{AC}{BC} = \frac{3}{5}$

Ta được hình vẽ:

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

Câu 4: Trang 69 sách VNEN 9 tập 1

Cho tam giác ABC vuông tại A, BC = 10 cm, cosB = 0,8.

a) Tính các cạnh AB, AC

b) Tính các tỉ số lượng giác của góc C.

Bài làm:

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

a) Ta có $cosB = 0,8 \Leftrightarrow \frac{AB}{BC} = \frac{4}{5} \Rightarrow AB = 8 cm$ $cosB = 0,8 \Leftrightarrow \frac{AB}{BC} = \frac{4}{5} \Rightarrow AB = 8 cm$

Áp dụng định lý Py-ta-go ta được $AC = \sqrt{BC^{2} - AC^{2}} = \sqrt{10^{2} - 8^{2}} = 6 cm.$ $AC = \sqrt{BC^{2} - AC^{2}} = \sqrt{10^{2} - 8^{2}} = 6 cm.$

b) Ta có:

$sinC = \frac{AB}{BC} = \frac{8}{10} = \frac{4}{5}$ $sinC = \frac{AB}{BC} = \frac{8}{10} = \frac{4}{5}$

$cosC = \frac{AC}{BC} = \frac{6}{10} = \frac{3}{5}$ $cosC = \frac{AC}{BC} = \frac{6}{10} = \frac{3}{5}$

$tanC = \frac{AB}{AC} = \frac{8}{6} = \frac{4}{3}$ $tanC = \frac{AB}{AC} = \frac{8}{6} = \frac{4}{3}$

$cotC = \frac{AC}{AB} = \frac{6}{8} = \frac{3}{4}.$ $cotC = \frac{AC}{AB} = \frac{6}{8} = \frac{3}{4}.$

D.E. Hoạt động vận dụng và tìm tòi, mở rộng

1. Trang 69 sách VNEN 9 tập 1

Em có biết?

Nhà mái ngói dốc (mái dốc) là một trong những hình thức kiến trúc phổ biến nhất ở Việt Nam. Mái dốc kiểu truyền thống phù hợp với cả kiến trúc phương Đông và phương Tây, phù hợp với khí hậu nhiệt đới móng ẩm của Việt Nam đồng thời lại tương đối rẻ tiền, dễ thi công. Mái dốc thường có ba loại sau đây (h.37)

Mái một dốc; Mái hai dốc; Mái bốn dốc.

Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN

Trong xây dựng, người ta thường sử dụng đến khái niệm "độ dốc" của mái ngói, được tính bằng công thức:

$P = tan\alpha = \frac{h}{a} ,$ $P = tan\alpha = \frac{h}{a} ,$

với h: chiều cao, a: cạnh đáy, P thường được tính theo đơn vị %.

a) Mái dốc là mái có độ dốc > 8%. Em hãy tính góc dốc $\alpha$ $\alpha$tối thiểu của mái dốc.

b) Một ngôi nhà lợp mái ngói hai dốc có độ dốc 50%. Biết chiều cao của mái dốc là 1,2m, Tính bề rộng phần mái dốc của ngôi nhà.

c) Liệu có tồn tại mái có độ dốc 100% không? Vì sao?

Bài làm:

a) Mái dốc là mái có độ dốc > 8%, tức là:

$P = tan\alpha = \frac{h}{a} > 8 \Leftrightarrow \alpha > 83^{\circ}$ $P = tan\alpha = \frac{h}{a} > 8 \Leftrightarrow \alpha > 83^{\circ}$

b) Ta có công thức tính độ dốc của mái là:

$P = tan\alpha = \frac{h}{a} \Leftrightarrow 50 = \frac{1,2}{a} \Leftrightarrow a = 0,024m = 2,4 cm.$ $P = tan\alpha = \frac{h}{a} \Leftrightarrow 50 = \frac{1,2}{a} \Leftrightarrow a = 0,024m = 2,4 cm.$

c) Giả sử tồn tại mái dốc 100%, tức là khi đó:

$P = tan\alpha = \frac{h}{a} = 100 \Leftrightarrow h = 100a.$ $P = tan\alpha = \frac{h}{a} = 100 \Leftrightarrow h = 100a.$

Giải bài 3: Tỉ số lượng giác của góc nhọn- Sách VNEN toán 9 tập 1 trang 66. Phần trên VnDoc đã hướng dẫn các bạn soạn Toán 9, trả lời các câu hỏi với lời giải chi tiết giúp các bạn nắm chắc kiến thức từ đó vận dụng tốt giải các bài tập Toán lớp 9. Chúc các bạn học tốt

.............................................

Ngoài Soạn Toán 9 bài 3 Tỉ số lượng giác của góc nhọn VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt

Chia sẻ, đánh giá bài viết

578

Bài trước

Bài sau