Bài làm:
a) Ta được bảng sau:
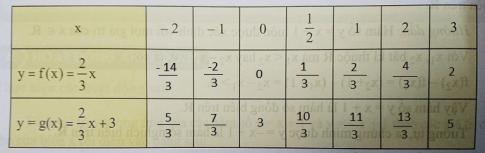
b) Hàm số y = f(x) là hàm số đồng biến. Vì khi các giá trị của x tăng dần thì các gái trị tương ứng của y tăng lên.
Soạn Toán 9 bài 4 Tính chất đồng biến, nghịch biến của hàm số y = ax + b VNEN
Soạn Toán 9 tập 1
VnDoc xin giới thiệu tới các bạn Soạn Toán 9 VNEN bài 4 Tính chất đồng biến, nghịch biến của hàm số y = ax + b. Hướng dẫn trả lời các câu hỏi nằm trong chương trình SGK VNEN lớp 9. Tài liệu này giúp các bạn củng cố kiến thức từ đó học tốt môn Toán lớp 9. Mời các bạn cùng tham khảo
Bài 4 Tính chất đồng biến, nghịch biến của hàm số y = ax + b VNEN
A. HOẠT ĐỘNG KHỞI ĐỘNG
Thực hiện các hoạt động sau
- Tính giá trị y tương ứng của các hàm số y = x + 1 và y = -x + 1 theo các giá trị đã cho của biến x rồi điền vào bảng sau:
x | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 |
y = x + 1 | |||||||||
y = -x + 1 |
- Quan sát bảng giá trị trên rồi trả lời các câu hỏi sau:
+) Đối với hàm số y = x + 1, khi cho x các giá trị tùy ý y tăng dần thì các giá trị tương ứng của y tăng lên hay giảm đi?
+) Đối với hàm số y = - x + 1, khi cho x các giá trị tùy ý y tăng dần thì các giá trị tương ứng của y tăng lên hay giảm đi?
Trả lời:
x | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 |
y = x + 1 | -1,5 | -1 | -0,5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 |
y = -x + 1 | 3.5 | 3 | 2.5 | 2 | 1.5 | 1 | 0.5 | 0 | -0.5 |
+) Đối với hàm số y = x + 1, khi cho x các giá trị tùy ý y tăng dần thì các giá trị tương ứng của y tăng lên.
+) Đối với hàm số y = - x + 1, khi cho x các giá trị tùy ý y tăng dần thì các giá trị tương ứng của y giảm đi.
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
2.c) Trong các hàm số sau, hàm số nào là đồng biến, nghích biến?
y = 8x - 5 ; y = -3x + 11 ; y = -49x - 100 ; y = 0,1 - 0,3x ; y = 0,3x + 0,1
Trả lời:
Các hàm số đồng biến là y = 8x - 5; y = 0,3x + 0,1
Các hàm sô nghich biến là y = -3x + 11; y = -49x - 100 ; y = 0,1 - 0,3x.
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 52 sách VNEN 9 tập 1
Cho hai hàm số 
\(y = f(x) = \frac{2}{3}x và y = g(x) = \frac{2}{3}x + 3\).
a) Tính giá trị tương ứng của mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:
b) Hàm số y = f(x) là hàm số đồng biến hay nghịch biến? Vì sao?
Câu 2: Trang 52 sách VNEN 9 tập 1
Cho hai hàm số y = 1,5x - 3 và y = -0,6x + 5.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đó.
b) Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
Bài làm:
a) Ta có đồ thị:
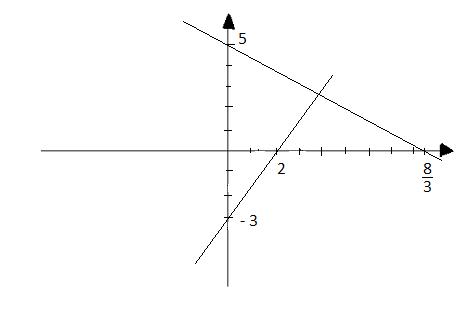
b)
* Hàm số y = 1,5x - 3 là hàm số đồng biến vì hàm số có hệ số góc a = 1,5 > 0
* Hàm số y = -0,6x + 5 là hàm số đồng biến vì hàm số có hệ số góc a = -0,6 < 0
Câu 3: Trang 52 sách VNEN 9 tập 1
Với giá trị nào của a hàm số y = (a - 2)x + 3:
a) Đồng biến? b) Nghích biến?
Bài làm:
a) Hàm số y = (a - 2)x + 3 đồng biến khi \(a - 2 > 0 \Leftrightarrow a > 2\)
b) Hàm số y = (a - 2)x + 3 nghịch biến khi \(a - 2 < 0 \Leftrightarrow a < 2.\)
Câu 4: Trang 52 sách VNEN 9 tập 1
Với giá trị nào của a thì điểm A(a; 2a - 1) thuộc đồ thị hàm số:
a) y = -2x + 3; b) y = -x + 5; c) f(x) = 3x - 1; d) \(f(x) = \frac{1}{3}x - \frac{2}{3}?\)
Bài làm:
a) Điểm A(a; 2a - 1) thuộc đồ thị hàm số y = -2x + 3 khi \(2a - 1 = -2a + 3 \Leftrightarrow a = 1\)
b) Điểm A(a; 2a - 1) thuộc đồ thị hàm số y = -x + 5 khi \(-a + 5 = 2a - 1 \Leftrightarrow a = 2\)
c) Điểm A(a; 2a - 1) thuộc đồ thị hàm số f(x) = 3x - 1 khi \(3a - 1 = 2a - 1 \Leftrightarrow a = 0\)
d) Điểm A(a; 2a - 1) thuộc đồ thị hàm số \(f(x) = \frac{1}{3}x - \frac{2}{3}\) khi \(\frac{1}{3}a - \frac{2}{3} = 2a - 1 \Leftrightarrow a = \frac{1}{5}.\)
D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG
Câu 1: Trang 52 sách VNEN 9 tập 1
Tìm tập xác định của mỗi hàm số sau:
a) y = -4x + 9; b) \(y = \frac{5}{x - 1}\);
c) \(y = \frac{x - 1}{x^{2} - 3x + 2}\); (HD: Phân tích mẫu thành nhân tử)
d) \(y = 1 - \sqrt{4 - x}\); e) \(y = \frac{5}{\sqrt{1 - 2x}}\)
Bài làm:
a) Tập xác định của hàm số y = -4x + 9 là D = R.
b) Tập xác định của hàm số\(y = \frac{5}{x - 1}\) là \(D = {x \in R|x \neq 1} = R*\)
c) \(y = \frac{x - 1}{x^{2} - 3x + 2} = \frac{x - 1}{(x - 2)(x - 1)} = \frac{1}{x - 2}.\)
Tập xác định của hàm số \(y = \frac{x - 1}{x^{2} - 3x + 2}\) là \(D = {x \in R|x \neq 2} = R*\)
d) Tập xác định của hàm số \(y = 1 - \sqrt{4 - x}\) là \(D = {x \in R|x \leq 4}\)
e) Tập xác định của hàm số \(y = \frac{5}{\sqrt{1 - 2x}}\) là \(D = {x \in R| x < \frac{1}{2}}\).
Câu 2: Trang 53 sách VNEN 9 tập 1
Hãy xét xem mỗi hàm số sau đồng biến hay nghịch biến?
a) y = 2x;
b) y = -2x;
c) \(y = \sqrt{x - 1} khi x \geq 1\) (Hướng dẫn: Sử dụng biểu thức liên hợp)
d) \(y = \sqrt{9 - x}\) khi \(x \leq 9\).
Bài làm:
a) Hàm số y = 2x là hàm số đồng biến vì hàm số có hệ số góc a = 2 > 0
b) Hàm số y = 2x là hàm số đồng biến vì hàm số có hệ số góc a = 2 > 0
c) Với x1, x2 bất kì thuộc R mà x1 , x2 hay x2 - x1 > 0, ta có:
\(y2 - y1 = \sqrt{x2 - 1} - \sqrt{x1 - 1} = \frac{x2 - 1 - x1 + 1}{\sqrt{x2 - 1} + \sqrt{x1 - 1}} = \frac{x2 - x1}{\sqrt{x2 - 1} + \sqrt{x1 - 1}} > 0\)
Vậy hàm số \(y = \sqrt{x - 1}\) là hàm số đồng biến
d) Với x1, x2 bất kì thuộc R mà x1 , x2 hay x2 - x1 > 0, ta có:
\(y2 - y1 = \sqrt{9 - x2} - \sqrt{9 - x1} = \frac{9 - x2 - 9 + x1}{\sqrt{9 - x2} + \sqrt{9 - x1}} = \frac{x1 - x2}{\sqrt{9 - x2} + \sqrt{9 - x1}} < 0\)
Vậy hàm số \(y = \sqrt{9 - x}\) là hàm số nghịch biến.
Giải bài 4 : Tính chất đồng biến, nghịch biến của hàm số y = ax + b - Sách VNEN toán 9 tập 1 trang 50. Phần trên VnDoc đã hướng dẫn các bạn soạn Toán 9, trả lời các câu hỏi với lời giải chi tiết giúp các bạn nắm chắc kiến thức từ đó vận dụng tốt giải các bài tập Toán lớp 9. Chúc các bạn học tốt
.............................................
Ngoài Soạn Toán 9 bài 4 Tính chất đồng biến, nghịch biến của hàm số y = ax + b VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt
