1. Điền vào chỗ chấm (...) để ôn tập các công thức đã học trong chương.
1.1. Các hệ thức về cạnh và đường cao trong tam giác vuông
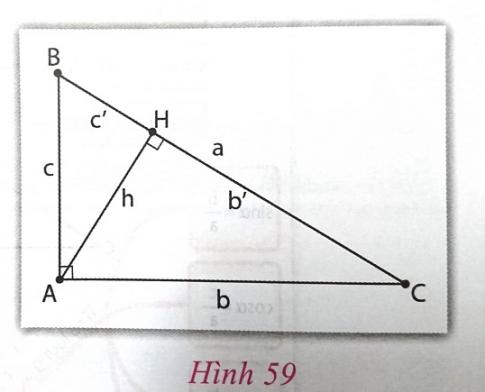
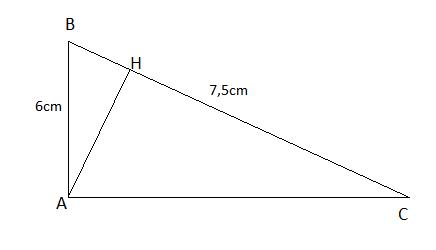
Cho tam giác ABC vuông tại A, đường cao AH (h.59)
![]() \(a) b^{2} = ab'; c^{2} = ac' ;\)
\(a) b^{2} = ab'; c^{2} = ac' ;\)
![]() \(b) h^{2} = b'c' ;\)
\(b) h^{2} = b'c' ;\)
![]() \(c) b.c = a.h;\)
\(c) b.c = a.h;\)
![]() \(d) \frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}\)
\(d) \frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}\)
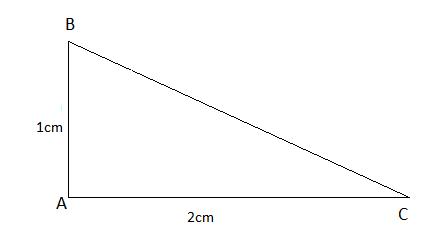
1.2. Định nghĩa các tỉ số lượng giác của góc nhọn \alpha (h.60)
 \(sin\alpha = \frac{cạnh đối}{cạnh huyền} ; cos\alpha = \frac{cạnh kề}{cạnh huyền} ;\)
\(sin\alpha = \frac{cạnh đối}{cạnh huyền} ; cos\alpha = \frac{cạnh kề}{cạnh huyền} ;\)
 \(tan\alpha = \frac{cạnh đối}{cạnh kề} ; cot\alpha = \frac{cạnh kề}{cạnh đối} .\)
\(tan\alpha = \frac{cạnh đối}{cạnh kề} ; cot\alpha = \frac{cạnh kề}{cạnh đối} .\)
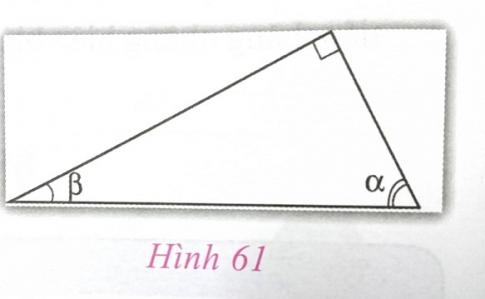
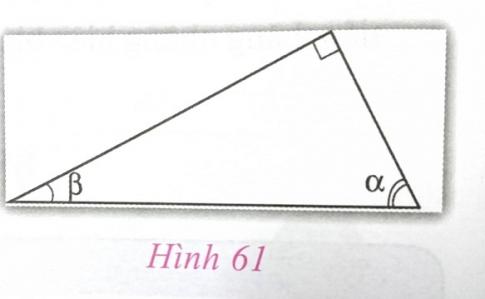
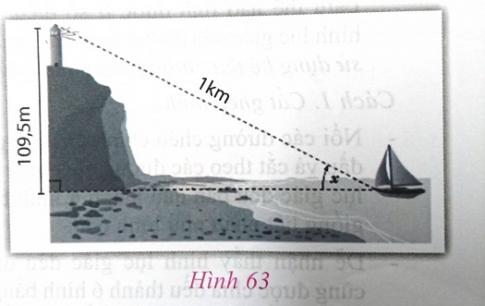
1.3. Một số tính chất của các tỉ số lượng giác (h.61)
* Cho hai góc \alpha phụ nhau. Khi đó
![]() \(sin\alpha = cos\beta ; tan\alpha = cot\beta ;\)
\(sin\alpha = cos\beta ; tan\alpha = cot\beta ;\)
![]() \(cos\alpha = sin\beta ; cot\alpha = tan\beta .\)
\(cos\alpha = sin\beta ; cot\alpha = tan\beta .\)
* Cho góc nhọn ![]() \(\alpha\). Ta có:
\(\alpha\). Ta có:
![]() \(0 < sin\alpha < 1 ; 0 < cos\alpha <1 ; sin^{2}\alpha + cos^{2}\alpha = 1 ;\)
\(0 < sin\alpha < 1 ; 0 < cos\alpha <1 ; sin^{2}\alpha + cos^{2}\alpha = 1 ;\)
![]() \(tan\alpha = \frac{sin\alpha}{cos\alpha} ; cot\alpha = \frac{cos\alpha}{sin\alpha} ; tan\alpha .cot\alpha = 1\)
\(tan\alpha = \frac{sin\alpha}{cos\alpha} ; cot\alpha = \frac{cos\alpha}{sin\alpha} ; tan\alpha .cot\alpha = 1\)
1.4. Các hệ thức về cạnh và góc trong tam giác vuông
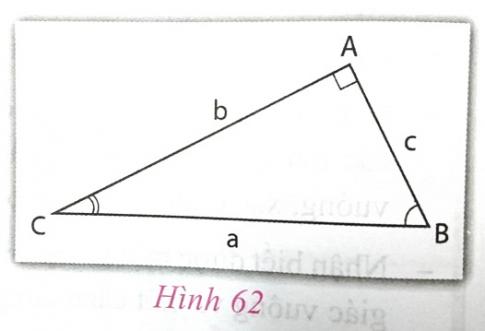
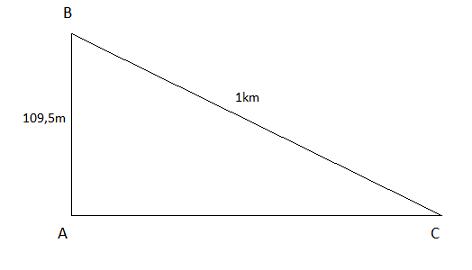
Cho tam giác ABC vuông tại A (h.62).
![]() \(a) b = a.sin B = a.cos C;\)
\(a) b = a.sin B = a.cos C;\)
![]() \(c = a.sin C = a.cos B\)
\(c = a.sin C = a.cos B\)
![]() \(b) b = c.tan B = c.cot C\)
\(b) b = c.tan B = c.cot C\)
![]() \(c = b.tan C = b.cot B\)
\(c = b.tan C = b.cot B\)