Soạn Toán 9 bài 2 Hệ số góc của đường thẳng y = ax + b VNEN

Soạn Toán 9 tập 1

Soạn Toán 9 VNEN bài 2 Hệ số góc của đường thẳng y = ax + b được VnDoc sưu tầm và đăng tải, hướng dẫn các bạn trả lời các câu hỏi nằm trong chương trinh SGK VNEN môn Toán lớp 9. Mời các bạn tham khảo để chuẩn bị tốt cho bài giảng sắp tới

Bài 2 Hệ số góc của đường thẳng y = ax + b VNEN

B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
C. HOẠT ĐỘNG LUYỆN TẬP
D. HOẠT ĐỘNG VẬN DỤNG
- Câu 1: Trang 44 sách VNEN 9 tập 1

A. HOẠT ĐỘNG KHỞI ĐỘNG

Thực hiện các hoạt động sau

Ví dụ 1: Cho hàm số y = x + 1

a) Vẽ đồ thị hàm số trên.

b) Tìm tọa độ giao điểm M của đường thẳng y = x + 1 với trục Ox và tọa độ giao điểm N của đường thẳng y = x + 1 với trục Oy.

c) Góc tạo bởi tia Mx và MN bằng bao nhiêu độ

Trả lời:

a) Cho x = 0 thì y = 1, ta được điểm A (0; 1)

Cho y = 0 thì x = - 1, ta được điểm B(-1; 0)

b) Đường thẳng y = x + 1 cắt Ox tại M(- 1; 0)

Đường thẳng y = x + 1 cắt Oy tại N(1; 0)

c) Tam giác OMN có OM = ON = 1 và OM vuông góc ON suy ra tam giác OMN là tam giác vuông cân

Vậy MN tạo với Mx một góc $45^{\circ}$ $45^{\circ}$

Ví dụ 2: Cho hàm số y = - x + 1

a) Vẽ đồ thị hàm số trên.

b) Tìm tọa độ giao điểm P của đường thẳng y = - x + 1 với trục Ox và tọa độ giao điểm Q của đường thẳng y = - x + 1 với trục Oy.

c) Góc tạo bởi tia Px và PQ bằng bao nhiêu độ.

Trả lời:

a) Cho x = 0 thì y = 1, ta được điểm A (0; 1)

Cho y = 0 thì x = 1, ta được điểm B(1; 0)

b) Đường thẳng y = - x + 1 cắt Ox tại P(1; 0)

Đường thẳng y = - x + 1 cắt Oy tại Q(1; 0)

c) Tam giác OPQ có OP = OQ = 1 và OMP vuông góc OQ suy ra tam giác OPQ là tam giác vuông cân

Suy ra $\widehat{OPQ} = 45^{\circ} \Rightarrow \widehat{QPx} = 135^{\circ}$ $\widehat{OPQ} = 45^{\circ} \Rightarrow \widehat{QPx} = 135^{\circ}$

Vậy PQ tạo với Px một góc $135^{\circ}$ $135^{\circ}$

B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

2.b) Thực hiện các hoạt động sau:

- Xác định hệ số a, b trong các hàm số đã cho rồi viết vào bảng sau:

- Nhận xét về liên hệ giữa hệ số a với góc tạo bởi mỗi đường thẳng trên với trục Ox.

Gợi ý: Khi hệ số a thay đổi thì độ lớn của góc $\alpha$ $\alpha$ và $\beta$ $\beta$ thay đổi như thế nào?

	a	b
y = 0,5x + 2
y = x + 2
y =2x + 2
y = -x + 2
y = -2x + 2
y = -0,5x + 2

Trả lời:

	a	b
y = 0,5x + 2	0,5	2
y =x + 2	1	2
y =2x + 2	2	2
y = -x + 2	-1	2
y = -2x + 2	-2	2
y = -0,5x + 2	-0,5	2

- Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn.

Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù.

Ví dụ

Ví dụ 1: Xác định hệ số góc của mỗi đường thẳng sau:

$f(x) = x - 3; y = 5 - x$; $h(x) = \frac{1}{\sqrt{3}}x + \sqrt{3}$ $h(x) = \frac{1}{\sqrt{3}}x + \sqrt{3}$

Trả lời:

Hệ số góc của đường thẳng f(x) = x - 3 là 1

Hệ số góc của đường thẳng y = 5 - x là - 1

Hệ số góc của đường thẳng $h(x) = \frac{1}{\sqrt{3}}x + \sqrt{3}$ $h(x) = \frac{1}{\sqrt{3}}x + \sqrt{3}$ là $\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$.

C. HOẠT ĐỘNG LUYỆN TẬP

Câu 1: Trang 43 sách VNEN 9 tập 1

Xác định hệ số góc của các đường thẳng sau:

$f(x) = -3x + 2; y = 4x + 17$; $f(x) = \frac{17}{18}x - \frac{7}{8}$ $f(x) = \frac{17}{18}x - \frac{7}{8}$; $g(x) = -0,4x - 0,05.$

Bài làm:

Hệ số góc của đường thẳng f(x) = -3x + 2 là -3

Hệ số góc của đường thẳng y = 4x + 17 là 4

Hệ số góc của đường thẳng $f(x) = \frac{17}{18}x - \frac{7}{8}$ $f(x) = \frac{17}{18}x - \frac{7}{8}$ là $\frac{17}{18}$ $\frac{17}{18}$

Hệ số góc của đường thẳng $g(x) = -0,4x - 0,05$ là $-0,4.$

Câu 2: Trang 43 sách VNEN 9 tập 1

Cho hàm số bậc nhất y = ax + 1.

a) Xác định hệ số góc a, biết rằng đồ thị hàm số đi qua điểm B(-1; 0,5).

b) Vẽ đồ thị hàm số với giá trị của a tìm được trong câu trên.

Bài làm:

y = ax + 1.

a) Đồ thị hàm số đi qua điểm B(-1; 0,5) tức là $0,5 = a.(-1) + 1 \Leftrightarrow a = 0,5$ $0,5 = a.(-1) + 1 \Leftrightarrow a = 0,5$

Vậy hệ số góc a = 0,5

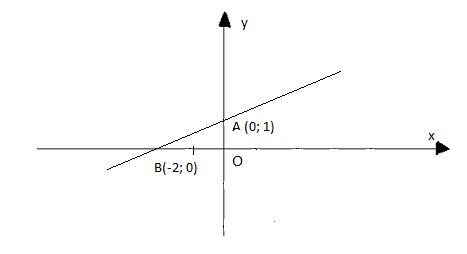
b) Ta có hàm số: y = 0,5x + 1

Cho x = 0 thì y = 1, ta có điểm A (0; 1)

Cho y = 0 thì x = - 2, ta có điểm B(-2; 0)

Soạn Toán 9 bài 2 Hệ số góc của đường thẳng y = ax + b VNEN

Câu 3: Trang 43 sách VNEN 9 tập 1

Xác định giá trị của b, biết đồ thị hàm số y = 7x + b đi qua điểm:

a) K(-1; 1); b) L(9; 0); c) M(0; 25)

Bài làm:

a) Đồ thị hàm số y = 7x + b đi qua điểm K(-1; 1) tức là $1 = 7.(-1) + b \Leftrightarrow b = 8$ $1 = 7.(-1) + b \Leftrightarrow b = 8$

b) Đồ thị hàm số y = 7x + b đi qua điểm L(9; 0) tức là $0 = 7.9 + b \Leftrightarrow b = -63$ $0 = 7.9 + b \Leftrightarrow b = -63$

c) Đồ thị hàm số y = 7x + b đi qua điểm M(0; 25) tức là $25 = 7.0 + b \Leftrightarrow b = 25.$ $25 = 7.0 + b \Leftrightarrow b = 25.$

Câu 4: Trang 43 sách VNEN 9 tập 1

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số:

$y = \frac{1}{2}x + 2$ $y = \frac{1}{2}x + 2$ và $y = -x + 2$

b) Gọi giao điểm của hai đường thẳng $y = \frac{1}{2}x + 2$ $y = \frac{1}{2}x + 2$ và $y = -x + 2$ với trục hoành theo thứ tự là A,B và gọi giao điểm của hai đường thẳng đó là C. Tính số đo góc A của tam giác ABC (làm tròn đến ohuts).

c) Tính chu vi và diện tích của tam giác ABC (đơn vị trên các trục tọa độ là xen-ti-mét).

Bài làm:

a)

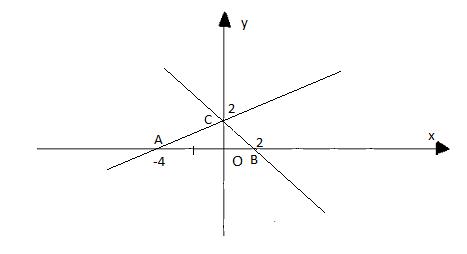
Soạn Toán 9 bài 2 Hệ số góc của đường thẳng y = ax + b VNEN

b)

Tam giác OAC có góc O vuông nên OAC là tam giác vuông

OA = 4; OC = 2 suy ra $AC = 2\sqrt{5}$ $AC = 2\sqrt{5}$

Ta có: $SinOAC = \frac{OC}{AC} = \frac{\sqrt{5}}{5}$ $SinOAC = \frac{OC}{AC} = \frac{\sqrt{5}}{5}$ suy ra $\widehat{OAC} = 26^{\circ}34$ $\widehat{OAC} = 26^{\circ}34'$

Vậy số đo góc A của tam giác ABC là $26^{\circ}34$ $26^{\circ}34'$

c) Tam giác ABC có $AC = 2\sqrt{5}cm, AB = 4 + 2 = 6cm, BC = 2\sqrt{2}cm$ $AC = 2\sqrt{5}cm, AB = 4 + 2 = 6cm, BC = 2\sqrt{2}cm$

Chu vi tam giác ABC là $C = AB + AC + BC = 6 + 2\sqrt{5} + 2\sqrt{2} = 13,3cm$ $C = AB + AC + BC = 6 + 2\sqrt{5} + 2\sqrt{2} = 13,3cm$

Diện tích tam giác ABC là: $S = \frac{1}{2}.OC.AB = \frac{1}{2}.2.6 = 6cm^{2}.$ $S = \frac{1}{2}.OC.AB = \frac{1}{2}.2.6 = 6cm^{2}.$

Câu 5: Trang 43 sách VNEN 9 tập 1

Xác định hệ số góc của các đường thẳng cho trên hình 7.

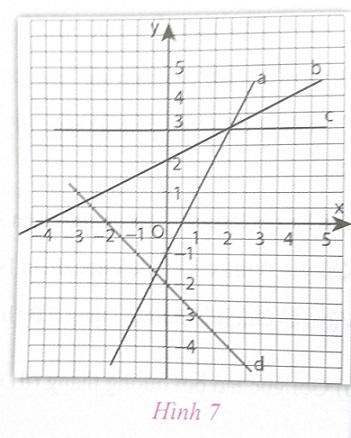
Soạn Toán 9 bài 2 Hệ số góc của đường thẳng y = ax + b VNEN

Bài làm:

Ta có hàm số (a): $y1 = ax + b$ đi qua các điểm (2; 3) và (0; -1)

Suy ra hàm số (a) là y = 2x - 1 có hệ số góc là 2

Tương tự hàm số (b) là y = 0,5x + 2 có hệ số góc là 0,5

Hàm số (c) là y = 3 có hệ số góc là 0

Hàm số (d) là y = -x - 2 có hệ số góc là -1.

D. HOẠT ĐỘNG VẬN DỤNG

Câu 1: Trang 44 sách VNEN 9 tập 1

Với giá trị nào của k, đồ thị hàm số y = kx + 8 đi qua điểm:

a) A(1; 12); b) B(-2; 0); c) C(0; 8).

Bài làm:

a) Đồ thị hàm số y = kx + 8 đi qua điểm A(1; 12) tức là $12 = k.1 + 8 \Rightarrow k = 4$ $12 = k.1 + 8 \Rightarrow k = 4$

b) Đồ thị hàm số y = kx + 8 đi qua điểm B(-2; 0) tức là $0 = k.(-2) + 8 \Rightarrow k = 4$ $0 = k.(-2) + 8 \Rightarrow k = 4$

c) Đồ thị hàm số y = kx + 8 đi qua điểm C(0; 8) tức là 8 = k.0 + 8(luôn đúng) suy ra với mọi k thì đồ thị hàm số y = kx + 8 luôn đi qua điểm C(0; 8).

Giải bài 2: Hệ số góc của đường thẳng y = ax + b- Sách VNEN toán 9 tập 1 trang 40. Phần trên VnDoc đã hướng dẫn các bạn soạn Toán 9, trả lời các câu hỏi với lời giải chi tiết giúp các bạn nắm chắc kiến thức từ đó vận dụng tốt giải các bài tập Toán lớp 9. Chúc các bạn học tốt

.............................................

Ngoài Soạn Toán 9 bài 2 Hệ số góc của đường thẳng y = ax + b VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt

Chia sẻ, đánh giá bài viết

1

417

Bài trước

Bài sau