VnDoc.com

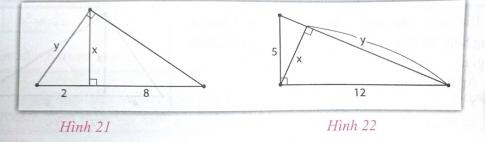
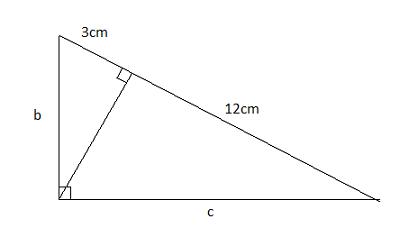
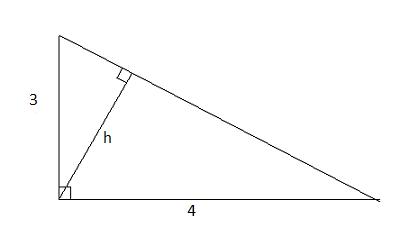
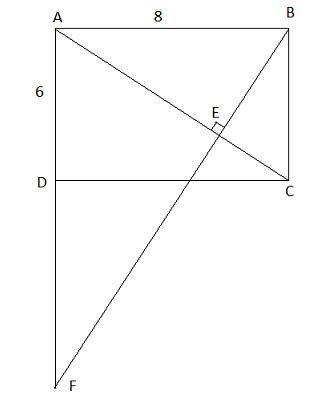
Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

Soạn Toán 9 tập 1 phần hình học

Bài trước

Bài sau

Bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

Soạn Toán 9 VNEN bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông được VnDoc sưu tầm và đăng tải. Hướng dẫn trả lời các câu hỏi nằm trong SGK VNEN lớp 9. Hy vọng với lời giải chi tiết sẽ giúp các bạn học tốt môn Toán lớp 9. Mời các bạn cùng tham khảo tài liệu dưới đây

A.B. Hoạt động khởi động và hình thành kiến thức

1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

a) Em thực hiện hoạt động sau

- Xem hình vẽ 16, chỉ ra tất cả các tam giác đồng dạng với tam giác ABH trong hình vẽ.

Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

- Dựa vào các tỉ số đồng dạng của các tam giác tìm được, em hoàn thành các đẳng thức sau:

$AC^{2} = CH x ............$ $AC^{2} = CH x ............$

$b^{2} = ........................ ;$ $b^{2} = ........................ ;$

$AB^{2} = BH x ............$ $AB^{2} = BH x ............$

$c^{2} = ........................$ $c^{2} = ........................$

Trả lời:

- Các tam giác đồng dạng với tam giác ABH là tam giác CBA, tam giác CAH.

$- AC^{2} = CH x CB$ $- AC^{2} = CH x CB$

$b^{2} = b$ $b^{2} = b'.(b' + c');$

$AB^{2} = BH x BC$ $AB^{2} = BH x BC$

$c^{2} = c$ $c^{2} = c'.(b' + c').$

c) Áp dụng công thức $b^{2} = ab$ $b^{2} = ab', c^{2} = ac'$ để làm bài tập sau

Bài tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6, BC = 10. Tính độ dài x, y trên hình 17. Điền vào chỗ chấm (....) để hoàn thành lời giải.

Gợi ý: Áp dụng công thức $b^{2} = ab$ $b^{2} = ab', c^{2} = ac'$ cho tam giác vuông..........., đường cao.......:

$+ AB^{2} = BH x ...... \Rightarrow 6^{2} = ..... x .......$ $+ AB^{2} = BH x ...... \Rightarrow 6^{2} = ..... x .......$

$\Rightarrow x =..... = ........$ $\Rightarrow x =..... = ........$

$+ y = BC - .....= 10 - ......$

Trả lời:

Áp dụng công thức $b^{2} = ab$ $b^{2} = ab', c^{2} = ac'$ cho tam giác vuông ABC đường cao AH:

$+AB^2=BH\times BC\Rightarrow6^2=x.(x+y)$ $+AB^2=BH\times BC\Rightarrow6^2=x.(x+y)$

$\Rightarrow x = \frac{6^{2}}{10}= 3,6$ $\Rightarrow x = \frac{6^{2}}{10}= 3,6$

$+y=BC-3,6=10-3,6=6,4.$

2. Một số hệ thức liên quan tới đường cao

a) Em điền vào chỗ chấm (....) để hoàn thành chứng minh sau

$\Delta ABH \sim \Delta CA (g.g) (h.18)$ $\Delta ABH \sim \Delta CA (g.g) (h.18)$

$\Rightarrow \frac{AH}{.....} = \frac{BH}{......} \Rightarrow AH^{2} = .......$ $\Rightarrow \frac{AH}{.....} = \frac{BH}{......} \Rightarrow AH^{2} = .......$

Trả lời:

$\Delta ABH \sim \Delta CAH (g.g) (h.18)$ $\Delta ABH \sim \Delta CAH (g.g) (h.18)$

$\Rightarrow \frac{AH}{HC} = \frac{BH}{AH} \Rightarrow AH^{2} = BH.CH.$ $\Rightarrow \frac{AH}{HC} = \frac{BH}{AH} \Rightarrow AH^{2} = BH.CH.$

b)

Bài tập 2: Áp dụng công thức $h^{2} = b$ $h^{2} = b'.c'$, tính x trong hình 19. Điền vào chỗ chấm (....) để hoàn thành lời giải

Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

Áp dụng công thức $h^{2} = b$ $h^{2} = b'.c'$, ta có:

$x^{2} = .......................................$ $x^{2} = .......................................$

$\Rightarrow x = .....................................$ $\Rightarrow x = .....................................$

Trả lời:

Áp dụng công thức $h^{2} = b$ $h^{2} = b'.c'$, ta có:

$x^{2} = 4.9$ $x^{2} = 4.9$

$\Rightarrow x = 6$ $\Rightarrow x = 6$

c)

Bài tập 3: Cho tam giác vuông với hai cạnh góc vuông lần lượt là 6cm và 8cm (h.20). Tính độ dài đường cao ứng với cạnh huyền của tam giác. Em hãy điền vào chỗ chấm(....) để hoàn thanh lời giải.

Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

Gợi ý: Theo định lý Py-ta-go

$BC^{2} = .....................= .................= ..............$ $BC^{2} = .....................= .................= ..............$

- Áp dụng công thức bc = ah, ta có:

$ABx............= ................xAH$

$\Rightarrow AH = \frac{.........x........}{..........} = \frac{...........}{..........} = ...................$ $\Rightarrow AH = \frac{.........x........}{..........} = \frac{...........}{..........} = ...................$

Trả lời:

Theo định lý Py-ta-go

$BC^{2} = AB^{2} + AC^{2} = 6^{2} + 8^{2} = 100.$ $BC^{2} = AB^{2} + AC^{2} = 6^{2} + 8^{2} = 100.$

- Áp dụng công thức bc = ah, ta có:

$AB.AC= BC.AH$

$\Rightarrow AH = \frac{AB.AC}{BC} = \frac{6.8}{10} = 4,8 cm$ $\Rightarrow AH = \frac{AB.AC}{BC} = \frac{6.8}{10} = 4,8 cm$

d)

Em hãy sử dụng công thức $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ để tính độ dài đường cao trong bai tập 3 và ghi vào vở.

- So sánh kết quả trên với các làm ở trên.

Trả lời:

Áp dụng công thức $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$, ta có:

$\frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}} = \frac{1}{6^{2}} + \frac{1}{8^{2}}$ $\frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}} = \frac{1}{6^{2}} + \frac{1}{8^{2}}$

$\Rightarrow AH = 4,8 cm.$ $\Rightarrow AH = 4,8 cm.$

- Kết quả tính AH ở hai cách làm bằng nhau.

C. Hoạt động luyện tập

Câu 1: Trang 60 sách VNEN 9 tập 1

Tính x, y trong mỗi hình sau:

Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

Bài làm:

* Hình 21

Áp dụng công thức $b^{2} = b$ $b^{2} = b'.a'$, ta có:

$y^{2} = 2.(2 + 8) = 20$ $y^{2} = 2.(2 + 8) = 20$

$\Rightarrow y = 2\sqrt{5}$ $\Rightarrow y = 2\sqrt{5}$

Áp dụng công thức $h^{2} = b$ $h^{2} = b'.c'$, ta có:

$x^{2} = 2.8 = 16$ $x^{2} = 2.8 = 16$

$\Rightarrow x = 4.$ $\Rightarrow x = 4.$

* Hình 22:

Áp dụng công thức $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$, ta có:

$\frac{1}{x^{2}} = \frac{1}{5^{2}} + \frac{1}{12^{2}}$ $\frac{1}{x^{2}} = \frac{1}{5^{2}} + \frac{1}{12^{2}}$

$\Rightarrow x = \frac{60}{13}$ $\Rightarrow x = \frac{60}{13}$

Áp dụng định lý Py-ta-go, ta có:

$y^{2} = 12^{2} - x^{2} = 12^{2} - (\frac{60}{13})^{2}$ $y^{2} = 12^{2} - x^{2} = 12^{2} - (\frac{60}{13})^{2}$

$\Rightarrow y = \frac{144}{13}.$ $\Rightarrow y = \frac{144}{13}.$

Câu 2: Trang 61 sách VNEN 9 tập 1

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 3cm và 12cm. Hãy vẽ hình và tính các cạnh góc vuông của tam giác này.

Bài làm:

Ta được hình vẽ:

Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

* Áp dụng công thức $c^{2} = c$ $c^{2} = c'.a$, ta có:

$c^{2} = 12.(12 + 3) = 180$ $c^{2} = 12.(12 + 3) = 180$

$\Rightarrow c = 6\sqrt{5} cm.$ $\Rightarrow c = 6\sqrt{5} cm.$

* Áp dụng công thức $b^{2} = b$ $b^{2} = b'.a$, ta có:

$b^{2} = 3.(12 + 3) = 45$ $b^{2} = 3.(12 + 3) = 45$

$\Rightarrow c = 3\sqrt{5} cm$ $\Rightarrow c = 3\sqrt{5} cm$

Câu 3: Trang 61 sách VNEN 9 tập 1

Nam vẽ một tam giác vuông trên giấy kẻ ô li, hai cạnh góc vuông nằm tương ứng trên hai đường kẻ dọc và ngang của quyển vở, lần lượt ứng với 3 ô li và 4 ô li. Tiếp theo Nam kẻ đường cao ứng với cạnh huyền. Tính độ dài đường cao đó.

Bài làm:

Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

Gọi đường cao của tam giác vuông Nam kẻ được là h

Áp dụng công thức $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$, ta có:

$\frac{1}{h^{2}} = \frac{1}{3^{2}} + \frac{1}{4^{2}} = \frac{25}{144}$ $\frac{1}{h^{2}} = \frac{1}{3^{2}} + \frac{1}{4^{2}} = \frac{25}{144}$

$\Rightarrow h = 2,4 cm$ $\Rightarrow h = 2,4 cm$

Câu 4: Trang 61 sách VNEN 9 tập 1

Cho hình chữ nhật ABCD có cạnh BC = 6cm, AB = 8cm. Đường thẳng kẻ từ B vuông góc với AC tại E, cắt cạnh AD tại F.

a) Tính độ dài các đoạn thẳng AC, AE, BE.

b) Tính độ dài các cạnh và diện tích tam giác ABF.

Bài làm:

Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN

$a) * AC^{2} = AB^{2} + BC^{2} = 6^{2} + 8^{2} = 100$ $a) * AC^{2} = AB^{2} + BC^{2} = 6^{2} + 8^{2} = 100$

$\Rightarrow AC = 10 cm$ $\Rightarrow AC = 10 cm$

* Áp dụng công thức $b^{2} = b.a$ $b^{2} = b.a'$, ta có:

$AB^{2} = AE.AC \Rightarrow AE = \frac{AB^{2}}{AC} = \frac{8^{2}}{10} = 6,4 cm.$ $AB^{2} = AE.AC \Rightarrow AE = \frac{AB^{2}}{AC} = \frac{8^{2}}{10} = 6,4 cm.$

* Áp dụng định lý Py-ta-go, ta có:

$BE^{2} = AB^{2} - AE^{2} = 8^{2} - 6,4^{2} = 23,04$ $BE^{2} = AB^{2} - AE^{2} = 8^{2} - 6,4^{2} = 23,04$

$\Rightarrow BE = 4,8 cm.$ $\Rightarrow BE = 4,8 cm.$

b) Tam giác ABF có cạnh AB = 8 cm

* Áp dụng công thức $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$, ta có:

$\frac{1}{AE^{2}} = \frac{1}{AB^{2}} + \frac{1}{AF^{2}}$ $\frac{1}{AE^{2}} = \frac{1}{AB^{2}} + \frac{1}{AF^{2}}$

$\Rightarrow \frac{1}{AF^{2}} = \frac{1}{AE^{2}} - \frac{1}{AB^{2}} = \frac{1}{6,4^{2}} - \frac{1}{8^{2}}$ $\Rightarrow \frac{1}{AF^{2}} = \frac{1}{AE^{2}} - \frac{1}{AB^{2}} = \frac{1}{6,4^{2}} - \frac{1}{8^{2}}$

$\Rightarrow AF = \frac{32}{3} = 10,7 cm.$ $\Rightarrow AF = \frac{32}{3} = 10,7 cm.$

* Áp dụng định lý Py-ta-go, ta có:

$BF^{2} = AB^{2} + AF^{2} = 8^{2} + (\frac{32}{3})^{2}$ $BF^{2} = AB^{2} + AF^{2} = 8^{2} + (\frac{32}{3})^{2}$

$\Rightarrow BF = \frac{40}{3} cm$ $\Rightarrow BF = \frac{40}{3} cm$

* Diện tích tam giác ABF là

$S = \frac{1}{2}.AB.AF = \frac{1}{2}.8.\frac{32}{3} = \frac{128}{3} cm^{2}.$ $S = \frac{1}{2}.AB.AF = \frac{1}{2}.8.\frac{32}{3} = \frac{128}{3} cm^{2}.$

Giải bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông - Sách VNEN toán 9 tập 1 trang 58. Phần trên VnDoc đã hướng dẫn các bạn soạn Toán 9, trả lời các câu hỏi với lời giải chi tiết giúp các bạn nắm chắc kiến thức từ đó vận dụng tốt giải các bài tập Toán lớp 9. Chúc các bạn học tốt

.............................................

Ngoài Soạn Toán 9 bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 9, Giải Vở BT Toán 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt