VnDoc.com

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Đề kiểm tra 15 phút Chương 5 Phương trình mặt phẳng, đường thẳng, mặt cầu CTST

Mô tả thêm:

Cùng nhau thử sức với bài kiểm tra 15 phút Toán 12 Chân trời sáng tạo Chương 5 Phương trình mặt phẳng, đường thẳng, mặt cầu nhé!

Thời gian làm: 15 phút
Số câu hỏi: 20 câu
Số điểm tối đa: 20 điểm
Tài khoản: Đăng nhập

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Câu 1: Nhận biết
Tính góc giữa hai mặt phẳng

Trong không gian $Oxyz$ cho hai mặt phẳng $(P):x + z + 4 = 0,(Q):x - 2y + 2z + 4 = 0$ . Góc giữa hai mặt phẳng $(P);(Q)$ bằng:
- A.
  $90^{0}$
- B.
  $30^{0}$
- C.
  $45^{0}$
- D.
  $60^{0}$
Ta có: $(P):x + z + 4 = 0$ có 1 vectơ pháp tuyến là $\overrightarrow{n_{1}} = (1;0;1)$

$(Q):x - 2y + 2z + 4 = 0$ có 1 vectơ pháp tuyến là $\overrightarrow{n_{2}} = (1; - 2;2)$

Khi đó:

$\cos\left( (P);(Q) ight) = \cos\left( \overrightarrow{n_{1}};\overrightarrow{n_{2}} ight)$ $= \frac{\left| \overrightarrow{n_{1}}.\overrightarrow{n_{2}} ight|}{\left| \overrightarrow{n_{1}} ight|.\left| \overrightarrow{n_{2}} ight|} = \frac{1}{\sqrt{2}}$

$\Rightarrow \left( (P);(Q) ight) = 45^{0}$
Câu 2: Thông hiểu

Xét tính đúng sai của các nhận định

Trong không gian $Oxyz$ , cho đường thẳng $\Delta:\left\{ \begin{matrix}x =3 - 2t \\y = 1 + 2t \\x = - 5 + t\end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)$ và mặt phẳng $(P):x + y - 5= 0$ .

a) Vectơ $\overrightarrow{u} = ( - 2;2;1)$ là một vectơ chỉ phương của $\Delta$ . Đúng||Sai

b) Góc giữa hai mặt phẳng $(P)$ và $(Oyz)$ bằng $45^{0}$ . Đúng||Sai

c) Đường thẳng đi qua $N(2;3; - 4)$ và song song với $\Delta$ có phương trình là $\frac{x - 2}{- 2} = \frac{y - 3}{2} = \frac{z + 4}{1}$ . Đúng||Sai

d) Đường thẳng d vuông góc $\Delta$ và tạo với $(P)$ một góc 45⁰ có một vectơ chỉ phương là $\overrightarrow{u_{1}} = (1; - 2;4)$ . Sai||Đúng

Đáp án là:

Trong không gian $Oxyz$ , cho đường thẳng $\Delta:\left\{ \begin{matrix}x =3 - 2t \\y = 1 + 2t \\x = - 5 + t\end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)$ và mặt phẳng $(P):x + y - 5= 0$ .

a) Vectơ $\overrightarrow{u} = ( - 2;2;1)$ là một vectơ chỉ phương của $\Delta$ . Đúng||Sai

b) Góc giữa hai mặt phẳng $(P)$ và $(Oyz)$ bằng $45^{0}$ . Đúng||Sai

c) Đường thẳng đi qua $N(2;3; - 4)$ và song song với $\Delta$ có phương trình là $\frac{x - 2}{- 2} = \frac{y - 3}{2} = \frac{z + 4}{1}$ . Đúng||Sai

d) Đường thẳng d vuông góc $\Delta$ và tạo với $(P)$ một góc 45⁰ có một vectơ chỉ phương là $\overrightarrow{u_{1}} = (1; - 2;4)$ . Sai||Đúng

a) Đúng

b) Đúng

c) Đúng

d) Sai

Phương án a) đúng: Từ phương trình của $\Delta:\left\{ \begin{matrix} x = 3 - 2t \\ y = 1 + 2t \\ x = - 5 + t \end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)$ ta có $\overrightarrow{u} = ( - 2;2;1)$ là một vectơ chỉ phương của $\Delta$ .

Phương án b) đúng: $(P):x + y - 5 = 0$ ; $(Oyz):x = 0$ nên ta có $\cos\left( (P);(Oyz) \right) = \frac{1}{\sqrt{2}}$ .

Suy ra $\left( (P);(Oyz) \right) =45^0$ .

Phương án c) đúng: Đường thẳng $\Delta_{1}// \Delta$ nên $\Delta_{1}$ nhận $\overrightarrow{u} = ( - 2;2;1)$ làm VTCP. Hơn nữa $\Delta_{1}$ đi qua $N(2;3; - 4)$ nên có phương trình là $\frac{x - 2}{- 2} = \frac{y - 3}{2} = \frac{z + 4}{1}$ .

Phương án d) sai: Gọi $\overrightarrow{u_{1}} = (a;b;c)$ (với $a^{2} + b^{2} + c^2 > 0$ ) là một VTCP của d. Do $d\bot\Delta$ nên $\overrightarrow{u_{1}}\bot\overrightarrow{u} \Rightarrow \overrightarrow{u_{1}}.\overrightarrow{u} = 0$

$\Rightarrow - 2a + 2b + c = 0 \Rightarrow c = 2a - 2b(*)$

Hơn nữa $\left( d;(P) \right) =45^0$ nên $\sin\left( d;(P) \right)= \frac{1}{\sqrt{2}} = \frac{|a + b|}{\sqrt{2}.\sqrt{a^{2} + b^{2} +c^{2}}}$

$\Leftrightarrow |a + b| = \sqrt{a^{2} + b^{2} + c^{2}}$

$\Leftrightarrow (a + b)^{2} = a^{2} + b^{2} + c^{2} \Leftrightarrow 2ab = c^{2}$

. Thay (*) vào ta được: $(2a - 2b)^{2} = 2ab \Leftrightarrow 2a^{2} - 5ab + 2b^{2} = 0(**)$

Nếu $b = 0 \Rightarrow a = 0;c = 0$ (không thỏa mãn).

Nếu $b \neq 0$ , ta có $(**) \Leftrightarrow 2.\left( \frac{a}{b} \right)^{2} - 5\left( \frac{a}{b} \right) + 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} \frac{a}{b} = 2 \\ \frac{a}{b} = \frac{1}{2} \end{matrix} \right.$ .

Với $\frac{a}{b} = 2 \Rightarrow a = 2b$ , thay vào (*) ta được $c = 2b$ . Do đó $\overrightarrow{u_{1}} = (2b;b;2b);(b \neq 0)$

Với $\frac{a}{b} = \frac{1}{2} \Rightarrow b = 2a$ , thay vào (*) ta được $c = - 2a$ . Do đó $\overrightarrow{u_{1}} = (a;2a; - 2a);(a \neq 0)$

Vậy $\overrightarrow{u_{1}} = (1; - 2;4)$ không là một VTCP của d.

Cách khác: Giả sử $\overrightarrow{u_{1}} = (1; - 2;4)$ là một VTCP của d. Khi đó $\sin\left( d;(P) \right) = \frac{\left| 1.1 + ( - 2).1 + 4.0 \right|}{\sqrt{1^{2} + ( - 2)^{2} + 4^{2}}.\sqrt{1^{2} + 1^{2}}} = \frac{1}{\sqrt{42}} \Rightarrow \left( d;(P) \right) \neq 45^{0}$ (mâu thuẫn).

Vậy $\overrightarrow{u_{1}} = (1;2;-4)$ không là một VTCP của d.
Câu 3: Thông hiểu
Chọn đáp án đúng

Trong không gian với hệ trục tọa độ $Oxyz$ , cho các điểm $A(5;1;3),B(1;2;6),C(5;0;4),D(4;0;6)$ . Viết phương trình mặt phẳng qua $D$ và song song với mặt phẳng $(ABC)$ .
- A.
  $x + y + z - 10 = 0$ .
- B.
  $x + y + z - 9 = 0$ .
- C.
  $x + y + z - 8 = 0$ .
- D.
  $x + 2y + z - 10 = 0$ .
Phương pháp tự luận

+) $\overrightarrow{AB} = ( - 4;1;3),\ \ \overrightarrow{AC} = (0; - 1;1) \Rightarrow \left\lbrack \overrightarrow{AB},\overrightarrow{AC} \right\rbrack = (4;4;4)$ .

+) Mặt phẳng đi qua $D$ có VTPT $\overrightarrow{n} = (1;1;1)$ có phương trình: $x + y + z - 10 = 0$ .

+) Thay tọa độ điểm $A$ vào phương trình mặt phẳng thấy không thỏa mãn.

Vậy phương trình mặt phẳng thỏa mãn yêu cầu bài toán là: $x + y + z - 10 = 0$ .

Phương pháp trắc nghiệm

Gọi phương trình mặt phẳng $(ABC)$ có dạng $Ax + By + Cz + D = 0$ .

Sử dụng MTBT giải hệ bậc nhất 3 ẩn, nhập tọa độ 3 điểm $A,B,C$ vào hệ, chọn $D = 1$ ta được $A = \frac{1}{9},B = \frac{1}{9},C = \frac{1}{9}$ . (Trong trường hợp chọn $D = 1$ vô nghiệm ta chuyển sang chọn $D = 0$ ).

Suy ra mặt phẳng $(ABC)$ có VTPT $\overrightarrow{n} = (1;1;1)$

Mặt phẳng đi qua $D$ có VTPT $\overrightarrow{n} = (1;1;1)$ có phương trình: $x + y + z - 10 = 0$ .

Thay tọa độ điểm $A$ vào phương trình mặt phẳng thấy không thỏa mãn.
Câu 4: Vận dụng
Tính góc giữa đường thẳng và mặt phẳng

Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $B$ , thỏa mãn điều kiện, $AB = BC = a$ , $AD = 2a$ , $SA$ vuông góc với mặt đáy $(ABCD)$ , $SA = a$ . Gọi $M,N$ lần lượt là trung điểm của $SB,CD$ . Tính cosin của góc giữa $MN$ và $(SAC)$ . (Làm tròn kết quả đến hàng phần trăm)
- A.
  $0,45$
- B.
  $0,56$
- C.
  $0,74$
- D.
  $0,63$
Chọn hệ trục tọa độ như hình vẽ

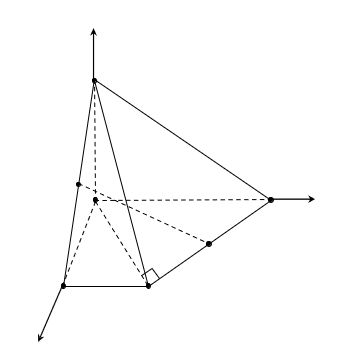
Chọn đơn vị là a

Có $A(0;0;0),B(1;0;0),C(1;1;0),D(0;2;0),S(0;0;1),M\left( \frac{1}{2};0;\frac{1}{2} \right),N\left( \frac{1}{2};\frac{3}{2};0 \right).$

Vecto chỉ phương của $\overrightarrow{MN}$ là $\overrightarrow{MN} = \left( 0;\frac{3}{2};\frac{- 1}{2} \right) \Rightarrow 2\overrightarrow{MN} = (0;3; - 1)$

Vecto pháp tuyến của $(SAC)$ là $\overrightarrow{n} = \left\lbrack \overrightarrow{AC},\overrightarrow{AS} \right\rbrack = (1; - 1;0)$

Vậy $\sin\left( MN,(SAC) \right) = \frac{|3|}{\sqrt{9 + 1}.\sqrt{2}} = \frac{3\sqrt{5}}{10}$

Suy ra: $\cos\left( MN,(SAC) \right) = \sqrt{1 - \left( \frac{3\sqrt{5}}{10} \right)^{2}} = \frac{\sqrt{55}}{10} \approx 0,74$
Câu 5: Vận dụng cao
Mối quan hệ giữa đường thẳng và mp

Cho 2 đường thẳng $(d)\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1 + t\\z = 1\end{array} ight.$ và $(\triangle )\left\{ \begin{array}{l}x = 1\\y = 1 + t\\z = 3 - t\end{array} ight.$
Mặt phẳng (P) chứa (d) và song song với $(\triangle )$ có phương trình tổng quát :
- A. $x - 2y + 2z - 2 = 0$
- B. $x + 2y + 2z + 2 = 0$
- C. $x + 2y - 2z + 2 = 0$
- D. $x - 2y - 2z - 2 = 0$
Phương trình (d) cho $A(2, - 1,1) \in (d)$ và vectơ chỉ phương của (d) là: $\overrightarrow a = (2,1,0)$
Phương trình $(\triangle )$ cho vectơ chỉ phương của $(\triangle )$ là : $\overrightarrow b = (0,1, - 1)$
Gọi $M(x,y,z)$ là điểm bất kỳ thuộc mặt phẳng (P) thì :
$\begin{array}{l}\overrightarrow {AM} = (x - 2,y + 1,z - 1);\,\,\,\,\left[ {\overrightarrow a ,\overrightarrow b } ight] = ( - 1,2,2)\\\left[ {\overrightarrow a ,\overrightarrow b } ight].\overrightarrow {AM} = 0 \Leftrightarrow - (x - 2) + 2(y + 1) + 2(z - 1) = 0\\ \Leftrightarrow x - 2y - 2z - 2 = 0\end{array}$
Câu hỏi này cho ta thấy mối quan hệ giữa đường thẳng và mặt phẳng, từ 2 đường thảng ta có thể viết PT được của 1 mp.
Câu 6: Nhận biết
Tính góc giữa hai đường thẳng

Trong không gian $Oxyz$ , cho hai đường thẳng $\Delta_{1}:\frac{x - 1}{- 2} = \frac{y + 2}{1} = \frac{z - 3}{2}$ và $\Delta_{2}:\frac{x + 3}{1} = \frac{y - 1}{1} = \frac{z + 2}{- 4}$ . Góc giữa hai đường thẳng $\Delta_{1};\Delta_{2}$ bằng?
- A.
  $30^{0}$ .
- B.
  $45^{0}$ .
- C.
  $60^{0}$ .
- D.
  $135^{0}$ .
Véc tơ chỉ phương của $\Delta_{1}$ là $\overrightarrow{u_{1}} = ( - 2;1;2)$

Véc tơ chỉ phương của $\Delta_{2}$ là $\overrightarrow{u_{2}} = (1;1; - 4)$

$\cos\left( \Delta_{1};\Delta_{2} \right) = \frac{\left| \overrightarrow{u_{1}}.\overrightarrow{u_{2}} \right|}{\left| \overrightarrow{u_{1}} \right|.\left| \overrightarrow{u_{2}} \right|} = \frac{\sqrt{2}}{2}$ .

Do đó góc giữa hai đường thẳng $\Delta_{1}$ và $\Delta_{2}$ là $45^{0}$
Câu 7: Nhận biết
Tìm vecto pháp tuyến của mặt phẳng

Trong không gian với hệ toạ độ $Oxyz$ , cho mặt phẳng (P) có phương trình $- 2x + 2y - z - 3 = 0$ . Mặt phẳng (P) có một vectơ pháp tuyến là:
- A.
  $\overrightarrow{n}(4; - 4;2)$ .
- B.
  $\overrightarrow{n}( - 2;2; - 3)$ .
- C.
  $\overrightarrow{n}( - 4;4;2)$ .
- D.
  $\overrightarrow{n}(0;0; - 3)$ .
Mặt phẳng (P) có phương trình $- 2x + 2y - z - 3 = 0$ có một vectơ pháp tuyến $\overrightarrow{n}(4; - 4;2)$
Câu 8: Thông hiểu

Xét sự đúng sai của các nhận định

Đúng||SaiTrong không gian $Oxyz$ , cho đường thẳng $d$ đi qua hai điểm $A(1;2;1)$ và $B(3;0;1)$ , mặt phẳng $(\alpha)$ đi qua ba điểm $M(0;1;0)$ , $N(2;1;3)$ , $P(4;1;1)$ .

a) Vectơ $\overrightarrow{AB}$ không là vectơ chỉ phương của đường thẳng $d$ . Sai||Đúng

b) $\overrightarrow{MN} = (2;0;3),\overrightarrow{MP} = (4;0;1)$ .

c) Mặt phẳng $(\alpha)$ có một vectơ pháp tuyến có toạ độ là $(0; - 1;0)$ . Đúng||Sai

d) Góc giữa đường thẳng $d$ và mặt phẳng $(\alpha)$ bằng $45^{o}$ . Đúng||Sai

Đáp án là:

Đúng||SaiTrong không gian $Oxyz$ , cho đường thẳng $d$ đi qua hai điểm $A(1;2;1)$ và $B(3;0;1)$ , mặt phẳng $(\alpha)$ đi qua ba điểm $M(0;1;0)$ , $N(2;1;3)$ , $P(4;1;1)$ .

a) Vectơ $\overrightarrow{AB}$ không là vectơ chỉ phương của đường thẳng $d$ . Sai||Đúng

b) $\overrightarrow{MN} = (2;0;3),\overrightarrow{MP} = (4;0;1)$ .

c) Mặt phẳng $(\alpha)$ có một vectơ pháp tuyến có toạ độ là $(0; - 1;0)$ . Đúng||Sai

d) Góc giữa đường thẳng $d$ và mặt phẳng $(\alpha)$ bằng $45^{o}$ . Đúng||Sai

Ta có: $\overrightarrow{AB} = (2\ \ ;\ \ - 2;\ \ 0)$ là một vectơ chỉ phương của đường thẳng $d;$

$\overrightarrow{MN} = (2\ \ ;\ \ 0;\ \ 3)$ , $\overrightarrow{MP} = (4\ \ ;\ \ 0;\ \ 1)$ và $\left\lbrack \overrightarrow{MN},\overrightarrow{MP} \right\rbrack = (0\ \ ;\ \ 10;\ \ 0)$ nên mặt phẳng $(\alpha)$ có một vectơ pháp tuyến là $\overrightarrow{n} = (0\ \ ;\ \ - 1;\ \ 0).$

Ta có: $\sin\left( d,(\alpha) \right) =\frac{\left| \overrightarrow{n}.\overrightarrow{AB} \right|}{\left|\overrightarrow{n} \right|.\left| \overrightarrow{AB} \right|}$ $=\frac{\left| 0.2 + ( - 1).( - 2) + 0.0 \right|}{\sqrt{0^{2} + ( - 1)^{2}+ 0^{2}}.\sqrt{2^{2} + ( - 2)^{2} + 0^{2}}} =\frac{\sqrt{2}}{2}$

Suy ra góc giữa đường thẳng d và mặt phẳng $(\alpha)$ bằng $45^{o}$ .

Đáp án: a) Sai, b) Đúng, c) Đúng, d) Đúng
Câu 9: Nhận biết
Tìm tham số m để hai đường thẳng vuông góc

Trong không gian với hệ tọa độ $Oxyz$ , cho 2 đường thẳng $d_{1}:\frac{x + 1}{2} = \frac{y - 1}{- m} =\frac{z - 2}{- 3};$ $d_{2}:\frac{x - 3}{1} = \frac{y}{1} = \frac{z -1}{1}$ . Tìm tất cả giá trị thực của $m$ để $d_{1}$ vuông góc với $d_{2}$ ?
- A.
  $m = - 1$
- B.
  $m = 1$
- C.
  $m = - 5$
- D.
  $m = 5$
Vectơ chỉ phương của $d_{1};d_{2}$ lần lượt là: $\overrightarrow{u_{1}} = (2; - m; - 3),\overrightarrow{u_{2}} = (1;1;1)$ .

Để $d_{1}\bot d_{2}$ thì $\overrightarrow{u_{1}}.\overrightarrow{u_{2}} = 0 \Leftrightarrow 2 - m - 3 = 0 \Leftrightarrow m = - 1$
Câu 10: Thông hiểu
Chọn phương án thích hợp

Hai mặt cầu $(S):x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0$ và $(S):x^{2} + y^{2} + z^{2} - 2a'x - 2b'y - 2c'z + d' = 0$ , cắt nhau theo đường tròn có phương trình: (Có thể chọn nhiều đáp án)
- A.
  $\left\{ \begin{matrix} x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0 \\ 2(a - a')x + 2(b - b')y + 2(c - c')z + d' - d = 0 \\ \end{matrix} \right.$
- B.
  $\left\{ \begin{gathered} {x^2} + {y^2} + {z^2} - 2a'x - 2b'y - 2c'z + d' = 0 \hfill \\ 2\left( {a - a'} \right)x + 2\left( {b - b'} \right)y + 2\left( {c - c'} \right)z + d' - d = 0 \hfill \\ \end{gathered} \right.$
- C.
  $\left\{ \begin{matrix} x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0 \\ 2(a - a')x + 2(b - b')y + 2(c - c')z + d - d' = 0 \\ \end{matrix} \right.$
Đáp án cần tìm là:

$\left\{ \begin{matrix} x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0 \\ 2(a - a')x + 2(b - b')y + 2(c - c')z + d' - d = 0 \\ \end{matrix} \right.$ và $\left\{ \begin{matrix} x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0 \\ 2(a - a')x + 2(b - b')y + 2(c - c')z + d - d' = 0 \\ \end{matrix} \right.$
Câu 11: Vận dụng cao
Xác định bán kính mặt cầu

Trong không gian với hệ tọa độ $Oxyz$ , cho hai điểm $S(0;0;1)$ và $A(1;1;1)$ . Hai điểm $M(m;0;0),N(0 ;n;0)$ thay đổi sao cho $m + n = 1$ và $m > 0,n > 0$ . Biết rằng luôn tồn tại một mặt cầu cố định đi qua $A$ và tiếp xúc với mặt phẳng $(SMN)$ . Bán kính của mặt cầu đó là:
- A.
  $\sqrt{2}$
- B.
  $2$
- C.
  $1$
- D.
  $\sqrt{3}$
Phương trình mặt phẳng $(SMN)$ là $\frac{x}{m} + \frac{y}{n} + \frac{z}{1} =1$
$\Leftrightarrow nx + my + mnz - mn =0$ .
Gọi $I(a;b;c)$ và $R$ là tâm và bán kính của mặt cầu cố định.
Ta có
$R = d(I;(SMN))$
$= \frac{|na + mb + mnc -mn|}{\sqrt{n^{2} + m^{2} + m^{2}n^{2}}}$
$= \frac{|(1 - m)a + mb + m(1 - m)(c -1)|}{\sqrt{1 - 2mn + m^{2}n^{2}}}$
$= \frac{|(1 - m)a + mb + m(1 - m)(c -1)|}{1 - mn}$
$= \frac{\left| (1 - c)m^{2} + (b + c - a- 1)m + a ight|}{m^{2} - m + 1}$
Mà $R$ không đổi nên $\frac{1 - c}{1} = \frac{b + c - a - 1}{- 1} =\frac{a}{1} = t \Rightarrow \left\{ \begin{matrix}a = t \\b = t \\c = 1 - t \\\end{matrix} ight.$ , hay $I(t;t;1- t)$ .
Mặt khác ta có $R = IA = \sqrt{3t^{3} - 4t +2} = |t| \Rightarrow t = 1$ .
Vậy $R = 1$ .
Câu 12: Thông hiểu
Viết phương trình (P)

Trong không gian với hệ toạ độ $Oxyz$ , cho hai điểm $A(1;2;1),B(3; - 1;5)$ . Phương trình mặt phẳng $(P)$ vuông góc với $AB$ và hợp với các trục tọa độ một tứ diện có thể tích bằng $\frac{3}{2}$ là
- A.
  $2x - 3y + 4z - 3 = 0$
- B.
  $2x - 3y + 4z + 3 = 0$
- C.
  $2x - 3y + 4z \pm 12 = 0$
- D.
  $2x - 3y + 4z \pm 6 = 0$
Ta có $\overrightarrow{AB} = (2; - 3;4) \Rightarrow (P):2x - 3y + 4z + m = 0$

Gọi M, N, P lần lượt là giao điểm của mặt phẳng (P) với trục Ox, Oy, Oz

Suy ra $M\left( - \frac{m}{2};0;0 ight),N\left( 0;\frac{m}{3};0 ight),P\left( 0;0;\frac{- m}{4} ight)$

Ta có thể tích tứ diện $V_{O.MNP} = \frac{1}{6}.\left| \frac{m^{3}}{24} ight| = \frac{3}{2} \Leftrightarrow m = \pm 6$

Vậy đáp án cần tìm là: $2x - 3y + 4z \pm 6 = 0$
Câu 13: Nhận biết
Viết phương trình tham số của đường thẳng

Trong không gian $Oxyz$ , cho đường thẳng $\Delta$ đi qua điểm $M(2;0; - 1)$ và có vectơ chỉ phương $\overrightarrow{a} = (4; - 6;2)$ . Phương trình tham số của đường thẳng $\Delta$ là:
- A.
  $\left\{ \begin{matrix} x = 2 + 2t \\ y = - 3t \\ z = - 1 + t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
- B.
  $\left\{ \begin{matrix} x = - 2 + 4t \\ y = - 6t \\ z = 1 + 2t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
- C.
  $\left\{ \begin{matrix} x = 4 + 2t \\ y = - 6 - 3t \\ z = 2 + t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
- D.
  $\left\{ \begin{matrix} x = 2 + 2t \\ y = - 3t \\ z = 1 + t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
Do $(2; - 2;1)$ cũng là vectơ chỉ phương nên phương trình tham số là: $\left\{ \begin{matrix} x = 2 + 2t \\ y = - 3t \\ z = - 1 + t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$ .
Câu 14: Nhận biết
Tìm khẳng định sai

Trong không gian với hệ toạ độ $Oxyz$ , cho mặt phẳng $(\alpha):Ax + By + Cz + D = 0$ . Tìm khẳng định sai trong các mệnh đề sau:
- A.
  $A = 0,B \neq 0,C \neq 0,D \neq 0$ khi và chỉ khi $(\alpha)$ song song với trục Ox.
- B.
  $D = 0$ khi và chỉ khi $(\alpha)$ đi qua gốc tọa độ.
- C.
  $A \neq 0,B = 0,C \neq 0,D = 0$ khi và chỉ khi $(\alpha)$ song song với mặt phẳng $(Oyz)$ .
- D.
  $A = 0,B = 0,C \neq 0,D \neq 0$ khi và chỉ khi $(\alpha)$ song song với mặt phẳng $(Oxy)$ .
Khẳng định sai: “ $A \neq 0,B = 0,C \neq 0,D = 0$ khi và chỉ khi $(\alpha)$ song song với mặt phẳng $(Oyz)$ .”
Câu 15: Thông hiểu
Tìm tâm mặt cầu

Cho các điểm $A(1;3;0)$ và $B(2;1;1)$ và đường thẳng $d:\frac{x}{2} = \frac{y - 3}{1} = \frac{z}{1}$ . Mặt cầu $(S)$ đi qua hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm của $(S)$ là:
- A.
  $(4;5;2).$
- B.
  $(6;6;3).$
- C.
  $(8;7;4).$
- D.
  $( - 4;1; - 2).$
Gọi $I(2t;3 + t;t)$ trên d vì $IA = IB \Rightarrow t = 4 \Rightarrow I(8;7;4).$
Câu 16: Vận dụng
Tìm tọa độ điểm M thỏa mãn biểu thức

Trong không gian với hệ trục tọa độ $Oxyz$ , cho ba điểm $A(0; - 2; - 1),B( - 2; - 4;3),C(1;3; - 1)$ và mặt phẳng $(P):x + y - 2z - 3 = 0$ . Tìm điểm $M \in (P)$ sao cho $|\overrightarrow{MA} + \overrightarrow{MB} + 2\overrightarrow{MC}|$ dạt giá trị nhỏ nhất.
- A.
  $M\left( \frac{1}{2};\frac{1}{2}; - 1 ight)$ .
- B.
  $M\left( - \frac{1}{2}; - \frac{1}{2};1 ight)$ .
- C.
  $M(2;2; - 4)$ .
- D.
  $M( - 2; - 2;4)$ .
Gọi $I$ là điểm sao cho $\overrightarrow{IA} + \overrightarrow{IB} + 2\overrightarrow{IC} = 0 \Rightarrow I(0;0;0)$ .

Từ đó:

$|\overrightarrow{MA} + \overrightarrow{MB} + 2\overrightarrow{MC}| = |4\overrightarrow{MI} + (\overrightarrow{IA} + \overrightarrow{IB} + 2\overrightarrow{IC})| = 4IM \geq 4IH$

với $H$ là hình chiếu của $I$ trên mặt phẳng $(P)$ .

Từ đó suy ra $|\overrightarrow{MA} + \overrightarrow{MB} + 2\overrightarrow{MC}|$ dạt giá trị nhỏ nhất khi và chỉ khi $M \equiv H$ .

Phương trình đường thẳng đi qua $I$ và vuông góc với mặt phẳng $(P)$ là: $\left\{ \begin{matrix} x = t \\ y = t \\ z = - 2t \\ \end{matrix} ight.$ .

Tọa độ diểm $H$ là nghiệm $(x;y;z)$ của hệ

$\left\{ \begin{matrix}x = t \\y = t \\z = - 2t \\x + y - 2z - 3 = 0 \\\end{matrix} \Leftrightarrow \left\{ \begin{matrix}x = \dfrac{1}{2} \\y = \dfrac{1}{2} \\z = - 1 \\t = \dfrac{1}{2} \\\end{matrix} ight.\ ight.$

Suy ra $H = \left( \frac{1}{2};\frac{1}{2}; - 1 ight)$ .

Vậy, tọa độ điểm $M$ cần tìm là $M = \left( \frac{1}{2};\frac{1}{2}; - 1 ight)$ .
Câu 17: Nhận biết
Viết phương trình mặt cầu (S)

Trong không gian $Oxyz$ , cho hai điểm $I(1;1;1)$ và $A(1;2;3)$ . Phương trình mặt cầu có tâm $I$ và đi qua $A$ là:
- A.
  $(x + 1)^{2} + (y + 1)^{2} + (z + 1)^{2} = 5$
- B.
  $(x + 1)^{2} + (y + 1)^{2} + (z + 1)^{2} = 29$
- C.
  $(x - 1)^{2} + (y - 1)^{2} + (z - 1)^{2} = 5$
- D.
  $(x - 1)^{2} + (y - 1)^{2} + (z - 1)^{2} = 25$
Ta có: $R = IA = \sqrt{(1 - 1)^{2} + (2 - 1)^{2} + (3 - 1)^{2}} = \sqrt{5}$

Vậy phương trình mặt cầu tâm $I$ và đi qua điểm $A$ có phương trình là:

$(x - 1)^{2} + (y - 1)^{2} + (z - 1)^{2} = 5$ .
Câu 18: Thông hiểu
Tính góc giữa hai mặt phẳng

Trong không gian với hệ toạ độ $Oxyz$ , cho $(P):x - 2y + 2z - 5 = 0,A( - 3;0;1),B(1; - 1;3)$ . Viết phương trình đường thẳng $d$ qua $A$ , song song với $(P)$ sao cho khoảng cách từ $B$ đến $d$ là lớn nhất.
- A.
  $\frac{x + 3}{1} = \frac{y}{- 1} = \frac{z - 1}{2}$
- B.
  $\frac{x + 3}{3} = \frac{y}{- 2} = \frac{z - 1}{2}$
- C.
  $\frac{x - 1}{1} = \frac{y}{- 2} = \frac{z - 1}{2}$
- D.
  $\frac{x + 3}{2} = \frac{y}{- 6} = \frac{z - 1}{- 7}$
Hình vẽ minh họa

Vì $( - 3 - 2\ .0 + 2\ .1 - 5).\left( 1 - 2.( - 1) + 2.3 - 5 ight) < 0$ nên hai điểm A, B khác phía so với (P).

Gọi H là hình chiếu của B lên d.

Ta có: BH ≤ BA nên khoảng cách BH từ B đến d lớn nhất khi và chỉ khi H trùng A.

Khi đó AB ⊥ d.

VTPT của (P) là $\overrightarrow{n} = (1; - 2;2),\overrightarrow{AB} = (4; - 1;2)$

VTCP của d là $\overrightarrow{u} = \left\lbrack \overrightarrow{n};\overrightarrow{AB} ightbrack = ( - 2;6;7)$

Mà d qua A(−3; 0; 1) nên phương trình đường thẳng d là: $\frac{x + 3}{2} = \frac{y}{- 6} = \frac{z - 1}{- 7}$
Câu 19: Nhận biết
Chọn đáp án thích hợp

Trong không gian với hệ trục tọa độ $Oxyz$ , phương trình nào sau đây không phải là phương trình của một mặt cầu?
- A.
  $x^{2} + y^{2} + z^{2} + x - 2y + 4z - 3 = 0$
- B.
  $2x^{2} + 2y^{2} + 2z^{2} - x - y - z = 0$
- C.
  $2x^{2} + 2y^{2} + 2z^{2} + 4x + 8y + 6z + 3 = 0$
- D.
  $x^{2} + y^{2} + z^{2} - 2x + 4y - 4z + 10 = 0$
Phương trình $(S):x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0$ là phương trình của một mặt cầu nếu $a^{2} + b^{2} + c^{2} - d > 0$ .

Vậy phương trình không phải phương trình mặt cầu là:

$x^{2} + y^{2} + z^{2} - 2x + 4y - 4z + 10 = 0$
Câu 20: Vận dụng
Chọn đáp án chính xác nhất

Trong không gian với hệ tọa độ $Oxyz$ , cho hai điểm $A(3;5; - 1),B(1;1;3)$ . Tìm tọa độ điểm $M$ thuộc $(Oxy)$ sao cho $\left| \overrightarrow{MA} + \overrightarrow{MB} ight|$ ngắn nhất.
- A.
  $( - 2; - 3;0)$
- B.
  $(2; - 3;0)$
- C.
  $( - 2;3;0)$
- D.
  $(2;3;0)$
Gọi $J(x; y; z)$ là điểm sao cho $\overrightarrow{JA} + \overrightarrow{JB} = \overrightarrow{0}$ Suy ra J(2; 3; 1).

Khi đó $\left| \overrightarrow{MA} + \overrightarrow{MB} ight| = \left| \overrightarrow{MJ} + \overrightarrow{JA} + \overrightarrow{MJ} + \overrightarrow{JB} ight| = 2\left| \overrightarrow{MJ} ight|$

Vậy $\left| \overrightarrow{MA} + \overrightarrow{MB} ight|$ đạt GTNN khi và chỉ khi $\left| \overrightarrow{MJ} ight|$ đạt GTNN hay M là hình chiếu của J lên mặt phẳng (Oxy).

Vậy M(2; 3; 0).

Chia sẻ bởi:
Khang Anh

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề kiểm tra 15 phút Chương 5 Phương trình mặt phẳng, đường thẳng, mặt cầu CTST

Chúc mừng Bạn đã hoàn thành bài!

Toán 12 - Chân trời sáng tạo

Đề thi HK1 Toán 12 Chân trời sáng tạo Đề 3

Đề thi HK1 Toán 12 Chân trời sáng tạo Đề 2

Đề thi HK1 Toán 12 Chân trời sáng tạo Đề 4

Đề thi HK1 Toán 12 Chân trời sáng tạo Đề 5

Đề thi HK1 Toán 12 Chân trời sáng tạo Đề 6

Đề thi HK1 Toán 12 Chân trời sáng tạo Đề 7