Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Khóa học Lớp 12 Toán 12 - Chân trời sáng tạo
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề kiểm tra 45 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST

Mô tả thêm:

Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 1: Ứng dụng đạo hàm để khảo sát hàm số Toán 12 sách Chân trời sáng tạo các em nhé!
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Thông hiểu

    Xác định tọa độ giao điểm

    Tìm tọa độ giao điểm của đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = \frac{x - 2}{x + 2}.

    TXĐ D\mathbb{= R}\backslash\left\{ - 2 ight\}.

    Dễ thấy đồ thị hàm số có TCĐ: x = - 2 và TCN: y = 1.

    Suy ra giao điểm của hai đường tiệm cận là ( - 2\ ;\ 1).

  • Câu 2: Nhận biết

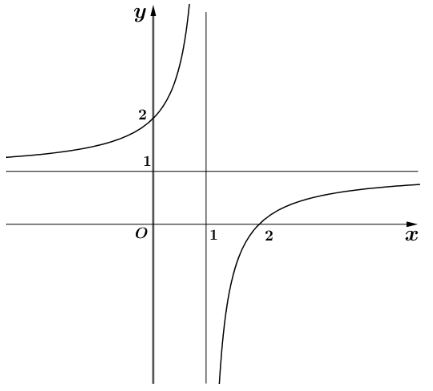
    Đường cong trong hình bên là đồ thị của hàm số nào?

    Trắc nghiệm Toán 12 bài 4

  • Câu 3: Vận dụng cao

    Tính số điểm cực trị của hàm số

    Cho hàm số y = f(x). Biết hàm số y = f’(x) có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số y = {2021^{f\left( x ight)}} + {2020^{f\left( x ight)}} là:

    Tính số điểm cực trị của hàm số

    Ta có:

    \begin{matrix} y' = f'\left( x ight){.2021^{f\left( x ight)}}.\ln 2021 + f'\left( x ight){.2020^{f\left( x ight)}}.\ln 2020 \hfill \\ = f'\left( x ight)\left[ {{{2021}^{f\left( x ight)}}.\ln 2021 + {{2020}^{f\left( x ight)}}.\ln 2020} ight] \hfill \\ \end{matrix}

    Do {2021^{f\left( x ight)}}.\ln 2021 + {2020^{f\left( x ight)}}.\ln 2020 > 0,\forall x \in \mathbb{R}

     y' = 0 \Leftrightarrow f'\left( x ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x_1} = a} \\ {{x_2} = b} \\ {{x_3} = c} \end{array}} ight.

    Tính số điểm cực trị của hàm số

    Vậy hàm số y = {2021^{f\left( x ight)}} + {2020^{f\left( x ight)}} có ba điểm cực trị.

  • Câu 4: Nhận biết

    Chọn đáp án chính xác

    Hàm số tương ứng với đồ thị trong hình vẽ dưới đây là:

    Từ đồ thị ta thấy đây là đồ thị hàm số bậc ba có dạng y = ax^{3} + bx^{2} + cx + d với a < 0 nên hàm số tương ứng là y = - x^{3} + 3x.

  • Câu 5: Nhận biết

    Chọn phương án thích hợp

    Biết rằng đường thẳng y = 4x + 5 cắt đồ thị hàm số y = x^{3} + 2x + 1 tại điểm duy nhất; kí hiệu (x_0;y_0) là tọa độ của điểm đó. Tìm y_0.

    Phương trình hoành độ giao điểm là x^{3} + 2x + 1 = 4x + 5

    \Leftrightarrow x^{3} - 2x - 4 = 0 \Leftrightarrow x = 2

    Với x = 2 \Rightarrow y = 13.

    Vậy y_{0} = 13

  • Câu 6: Thông hiểu

    Chọn khẳng định đúng

    Cho hàm số y = f(x) có bảng biến thiên sau:

    Khẳng định nào sau đây là đúng?

    "Hàm số có hai điểm cực trị" sai vì hàm số có ba điểm cực trị là x = - 1;\ x = 0;\ x = 1.

    "Hàm số đạt giá trị lớn nhất bằng - 3." sai vì hàm số không có giá trị lớn nhất.

    "Hàm số có một điểm cực tiểu" sai vì hàm số có hai điểm cực tiểu là x = - 1 và x = 1.

  • Câu 7: Vận dụng

    Tìm tập hợp tham số m thỏa mãn điều kiện

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f\left( \sin x \right) = m có nghiệm thuộc khoảng (0;\pi) là

    Đặt t = \sin x \Rightarrow \forall x \in (0;\pi) \Rightarrow t \in (0;1brack

    Vậy phương trình trở thành f(t) = m.

    Dựa và đồ thị hàm số suy ra m \in \lbrack - 1;1).

  • Câu 8: Vận dụng

    Tìm m thỏa mãn điều kiện

    Cho hàm số y = - x^{3} + 3mx^{2} - 3m -1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d:x + 8y - 74 = 0.

    Ta có y' = - 3x^{2} + 6mx = - 3x(x - 2m)

    y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2m \\ \end{matrix} ight..

    Để đồ thị hàm số có hai điểm cực trị \Leftrightarrow m eq 0.

    Khi đó gọi A(0; - 3m - 1) và B\left( 2m;4m^{3} - 3m - 1 ight) là hai điểm cực trị của đồ thị hàm số.

    Suy ra trung điểm của AB là điểm I\left( m;2m^{3} - 3m - 1 ight)và\overrightarrow{AB} = \left( 2m;4m^{3} ight) = 2m\left( 1;2m^{2} ight).

    Đường thẳng d có một vectơ chỉ phương là \overrightarrow{u} = (8; - 1).

    Ycbt \Leftrightarrow \left\{ \begin{matrix} I \in d \\ \overrightarrow{AB}.\overrightarrow{u} = 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m + 8\left( 2m^{3} - 3m - 1 ight) - 74 = 0 \\ 8 - 2m^{2} = 0 \\ \end{matrix} ight.\ \Leftrightarrow m = 2

  • Câu 9: Thông hiểu

    Tìm m để phương trình có hai nghiệm phân biệt

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có bảng biến thiên như hình vẽ. Tìm tất cả các giá trị của tham số m để phương trình f\left( x ight) = 2m có đúng hai nghiệm phân biệt.

    Tìm m để phương trình có hai nghiệm phân biệt

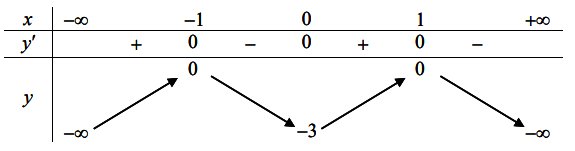
    Để phương trình f\left( x ight) = 2m có hai nghiệm phân biệt thì \left[ {\begin{array}{*{20}{c}} {2m = 0} \\ {2m < - 3} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {m = 0} \\ {m < \dfrac{{ - 3}}{2}} \end{array}} ight.

  • Câu 10: Vận dụng cao

    Ghi đáp án đúng vào ô trống

    Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.

    Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = g(x) = \frac{(x + 1)\left( x^{2} - 1 ight)}{f^{2}(x) - 2f(x)} là bao nhiêu?

    Đáp án: 6

    Đáp án là:

    Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.

    Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = g(x) = \frac{(x + 1)\left( x^{2} - 1 ight)}{f^{2}(x) - 2f(x)} là bao nhiêu?

    Đáp án: 6

    Ta có: f^{2}(x) - 2f(x) = 0\Leftrightarrow \left\lbrack \begin{matrix}f(x) = 0\ \ \ (1) \\f(x) = 2\ \ \ (2) \\\end{matrix} ight.

    Dựa vào đồ thị hàm số, ta thấy:

    (1) có nghiệm x_{1} = a < - 1 (nghiệm đơn) và x_{2} = 1 (nghiệm kép)

    \Rightarrow f(x) = k(x - a)(x - 1)^{2}(k > 0)

    (2) có nghiệm ba nghiệm đơn x_{1},x_{2},x_{3} với x_{1} = b < - 1 < x_{2} = 0 < 1 < x_{3} = c\ \ \ (b > a)

    \Rightarrow f(x) - 2 = k(x - b)x(x - c)(k > 0).

    \Rightarrow Hàm số y = g(x) có tập xác định D\mathbb{= R}\backslash\left\{ a;b;0;1;c ight\}

    +) Tìm tiệm cận ngang:

    Vì g(x) = \frac{(x + 1)\left( x^{2} - 1 ight)}{f^{2}(x) - 2f(x)} = \frac{(x + 1)\left( x^{2} - 1 ight)}{f(x)\left\lbrack f(x) - 2 ightbrack} = \frac{(x + 1)^{2}}{k^{2}(x - 1)(x - b)x(x - c)(x - a)}

    Nên \lim_{x ightarrow + \infty}g(x) = 0,\lim_{x ightarrow - \infty}g(x) = 0 \Rightarrow Đồ thị hàm số y = g(x) nhận đường thẳng y = 0 làm TCN.

    +) Tìm tiệm cận đứng:

    Tại các điểm x = a,x = b,x = 0,x = 1,x = c mẫu của g(x) nhận giá trị bằng 0 còn tử nhận các giá trị khác 0.

    Và do hàm số xác định trên D\mathbb{=R}\backslash\left\{ a; b ; 0; 1; c ight\} nên giới hạn một bên của hàm số y = g(x) tại các điểm x = a,x = b,x = 0,x = 1,x = c là các giới hạn vô cực.

    Do đó, đồ thị hàm số y = g(x) có 5 TCĐ: x = a,x = b,x = 0,x = 1 và x = c.

    Vậy ĐTHS y = g(x) có 6 đường tiệm cận: 1 TCN: y = 0 và 5 TCĐx = a,x = b,x = 0,x = 1,x = c.

  • Câu 11: Nhận biết

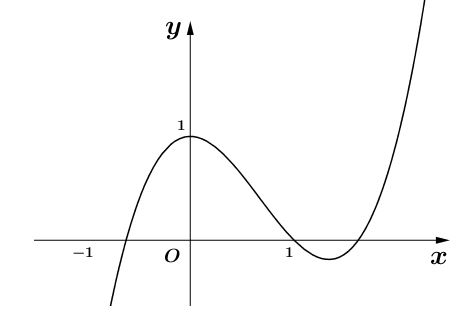
    Tìm hàm số đồng biến trên R

    Trong các hàm số dưới đây, hàm số nào đồng biến trên \mathbb{R}?

     Hàm số y = x – sinx có tập các định D = \mathbb{R} và y' = 1 - \cos x \geqslant 0, \vee x \in \mathbb{R}

    Nên hàm số luôn đồng biến trên \mathbb{R}

  • Câu 12: Thông hiểu

    Chọn mệnh đề đúng

    Cho hàm số y = x^{4} - 2x^{2} + 2. Mệnh đề nào dưới đây đúng?

    Xét y' = 0 \Leftrightarrow 4x^{3} - 4x = 0\Leftrightarrow \left\lbrack \begin{matrix} x = 1 \Rightarrow y = 1 \\ x = 0 \Rightarrow y = 2 \\ x = - 1 \Rightarrow y = 1 \\ \end{matrix} ight..

    Bảng biến thiên:

    Dựa vào bảng biến thiên ta thấy, hàm số đồng biến trên khoảng (2; + \infty).

  • Câu 13: Vận dụng

    Chọn phương án đúng

    Cho hàm số y = f(x)có bảng xét dấu đạo hàm như sau:

    Hàm số g(x) = f\left( 3 - 2^{x} \right)đồng biến trên khoảng nào sau đây

    Ta có g'(x) = - 2^{x}ln2.f'\left( 3 - 2^{x} ight).

    Để g(x) = f\left( 3 - 2^{x} ight)đồng biến thì

    g'(x) = - 2^{x}ln2.f'\left( 3 - 2^{x} ight) \geq 0 \Leftrightarrow f'\left( 3 - 2^{x} ight) \leq 0

    \Leftrightarrow - 5 \leq 3 - 2^{x} \leq 2 \Leftrightarrow 0 \leq x \leq 3.

    Vậy hàm số đồng biến trên (1;\ 2).

  • Câu 14: Thông hiểu

    Chọn mệnh đề đúng

    Cho hàm số y = x^{3} - 3x^{2}. Mệnh đề nào dưới đây đúng?

    Ta có y' = 3x^{2} - 6x; y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} ight..

    Lập bảng biến thiên rồi suy ra hàm số nghịch biến trên khoảng (0;2).

  • Câu 15: Nhận biết

    Tìm tiệm cận ngang của đồ thị hàm số

    Đường tiệm cận ngang của đồ thị hàm số y = \frac{x + 1}{x^{2} - 4} có phương trình là:

    Ta có: \lim_{x ightarrow \pm \infty}y = \lim_{x ightarrow \pm \infty}\frac{x + 1}{x^{2} - 4} = 0

    Vậy đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số.

  • Câu 16: Nhận biết

    Tìm số điểm cực trị của hàm số

    Cho hàm số y = f(x) xác định trên \mathbb{R} và có đạo hàm f'(x) = x(x - 1)^{3}(x + 2)^{2}. Tìm số điểm cực trị của hàm số đó?

    Ta có: f'(x) = x(x - 1)^{3}(x + 2)^{2} nên f'(x) = 0 có các nghiệm là x = 0;x = 1;x = - 2 và f'(x) chỉ đổi dấu khi x qua các nghiệm x = 0;x = 1

    Vậy hàm số đã cho có hai điểm cực trị.

  • Câu 17: Thông hiểu

    Tìm phương án đúng

    Cho hàm số f(x) có đạo hàm f'(x) = x(x + 1)^{2},\ \forall x\mathbb{\in R}. Số điểm cực trị của hàm số đã cho là

    Ta có

    f'(x) = 0 \Leftrightarrow x(x + 1)^{2} = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ (x + 1)^{2} = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = - 1 \\ \end{matrix} ight.

    Vì nghiệm x = 0 là nghiệm bội lẻ và x = - 1 là nghiệm bội chẵn nên số điểm cực trị của hàm số là 1.

  • Câu 18: Nhận biết

    Cho hàm số y = f(x) có đồ thị sau:

    Toán 12 bài 2

    Giá trị lớn nhất của hàm số trên đoạn [0;1] là:

  • Câu 19: Vận dụng cao

    Chọn đáp án đúng:

    Xét hàm số  y = f(x) = \left | x^{4}-4x^{3} +4x+a \right |. Gọi M,m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc [-4;4] sao cho M \leq 2m?

  • Câu 20: Nhận biết

    Chọn khẳng định đúng

    Cho hàm số f(x) xác định, liên tục trên tập số thực và đồ thị của hàm số f'(x) là đường cong như hình vẽ bên dưới.

    Khẳng định nào sau đây là khẳng định đúng?

    Từ đồ thị của hàm số f'(x) ta có:

    f'(x) \leq 0;\forall x \in ( - \infty; - 3) \cup ( - 2; + \infty)

    Vậy hàm số y = f(x) nghịch biến trên khoảng (0; + \infty).

  • Câu 21: Thông hiểu

    Tìm số đường thẳng thõa mãn yêu cầu

    Cho hàm số y = \frac{x + 1}{x - 3} có đồ thị (C) và các đường thẳng d_{1}:y = 2x, d_{2}:y = 2x - 2, d_{3}:y = 3x + 3, d_{4}:y = - x + 3. Hỏi có bao nhiêu đường thẳng trong bốn đường thẳng d_{1},d_{2},d_{3},d_{4} đi qua giao điểm của (C) và trục hoành.

    Ta có (C) cắt trục hoành (y - 0) tại điểm M( - 1;0).

    Trong các đường thẳng d_{1},d_{2},d_{3},d_{4}chỉ có M \in d_{3}, có nghĩa là có 1 đường thẳng đi qua M( - 1;0).

  • Câu 22: Nhận biết

    Chọn đáp án đúng

    Tiệm cận đứng của đồ thị hàm số y = \frac{x + 1}{x + 3} là

    Ta có \lim_{x ightarrow - 3^{+}}y = -\infty và \lim_{x ightarrow -3^{-}}y = + \infty nên đồ thị hàm số nhận đường thẳng x = - 3 làm tiệm cận đứng.

  • Câu 23: Thông hiểu

    Tìm giá trị lớn nhất nhỏ nhất của hàm số

    Cho hàm số f(x) = \frac{2x^{2} + x + 1}{x + 1}. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn \lbrack 0;1brack.

    Đạo hàm f'(x) = \frac{2x^{2} + 4x}{(x+ 1)^2}.

    Ta có \left\{ \begin{matrix} f'(x) \geq 0,\ \forall x \in \lbrack 0;1brack \\ f'(x) = 0 \Leftrightarrow x = 0 \\ \end{matrix} ight..

    Suy ra hàm số f(x) đồng biến trên đoạn \lbrack 0;1brack.

    Vậy \left\{ \begin{matrix} M = \max_{\lbrack 0;1brack}f(x) = f(1) = 2 \\ m = \min_{\lbrack 0;1brack}f(x) = f(0) = 1 \\ \end{matrix} ight.

  • Câu 24: Nhận biết

    Tìm điều kiện của tham số m

    Tất cả các giá trị của tham số m để hàm số y = x^{3} - 3x^{2} + mx + 5 có hai điểm cực trị?

    Ta có: y' = 3x^{2} - 6x + m

    Để hàm số có hai điểm cực trị thì y' = 0 có hai nghiệm phân biệt khi đó

    \Delta'_{y'} = 9 - 3m > 0 \Leftrightarrow m < 3

  • Câu 25: Nhận biết

    Tìm cực đại của hàm số

    Cho hàm số y = f(x) có đạo hàm f'(x) = x(x - 1)(x - 2);\forall x\mathbb{\in R}. Tìm số điểm cực đại của hàm số đã cho.

    Ta có: f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ x = 2 \\ \end{matrix} ight.

    Ta có bảng xét dấu:

    Suy ra hàm số có một điểm cực đại.

  • Câu 26: Vận dụng

    Ghi đáp án vào ô trống

    Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200m^{2}. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 300 nghìn đồng/m2. Hãy xác định chi phí thấp nhất để xây bể.

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200m^{2}. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 300 nghìn đồng/m2. Hãy xác định chi phí thấp nhất để xây bể.

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 27: Thông hiểu

    Ghi đáp án vào ô trống

    Lợi nhuận một xưởng thu được từ việc sản xuất một mặt hàng được cho bởi công thức P(x) = - x^{3} + 24x^{2} + 780x - 1000 trong đó x là khối lượng sản phẩm sản xuất được. Xưởng chỉ sản xuất tối đa 40 tạ sản phẩm trong một tuần. Hỏi để có lợi nhuận lớn nhất thì xưởng cần sản xuất bao nhiêu tạ sản phẩm trong một tuần?

    Đáp án: 26

    Đáp án là:

    Lợi nhuận một xưởng thu được từ việc sản xuất một mặt hàng được cho bởi công thức P(x) = - x^{3} + 24x^{2} + 780x - 1000 trong đó x là khối lượng sản phẩm sản xuất được. Xưởng chỉ sản xuất tối đa 40 tạ sản phẩm trong một tuần. Hỏi để có lợi nhuận lớn nhất thì xưởng cần sản xuất bao nhiêu tạ sản phẩm trong một tuần?

    Đáp án: 26

    Ta có P'(x) = - 3x^{2} + 48x + 780;\ \ P'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 10 \\ x = 26\ \ \ \\ \end{matrix} ight..

    Bảng biến thiên

    Vậy để lợi nhuận lớn nhất thì xưởng cần sản xuất 26 tạ sản phẩm trong một tuần.

  • Câu 28: Nhận biết

    Tính tổng m + M

    Cho hàm số f(x) liên tục trên đoạn \lbrack 0\ ;\ 3brack và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên \lbrack 0\ ;\ 3brack. Giá trị của M + m bằng?

    Dựa vào hình vẽ ta có: M = 3, m = - 2 nên M + m = 1.

  • Câu 29: Thông hiểu

    Chọn đáp án đúng:

    Cho hàm số y = f(x) = \frac{ax+1}{cx-1}. Nếu đồ thị hàm số có tiệm cận ngang y = 1 và tiệm cận đứng x = \frac{1}{2} thì giá trị của a và c là:

  • Câu 30: Nhận biết

    Chọn hàm số tương ứng với đồ thị

    Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

    Đồ thị hàm số là hàm số bậc 4 với \left\{ \begin{matrix} a < 0 \\ ab < 0 \\ \end{matrix} ight..

  • Câu 31: Vận dụng cao

    Tìm khoảng đồng biến của hàm số

    Cho hàm số đa thức f(x) có đạo hàm trên \mathbb{R}. Biết f(0) = 0 và đồ thị hàm số y = f'(x) như hình sau.

    Hàm số g(x) = \left| 4f(x) + x^{2} \right| đồng biến trên khoảng nào dưới đây?

    Xét hàm số h(x) = 4f(x) + x^{2} trên \mathbb{R}.

    Vì f(x) là hàm số đa thức nên h(x) cũng là hàm số đa thức và h(0) = 4f(0) = 0.

    Ta có h'(x) = 4f'(x) + 2x.

    Do đó h'(x) = 0 \Leftrightarrow f'(x) = - \frac{1}{2}x.

    Dựa vào sự tương giao của đồ thị hàm số y = f'(x) và đường thẳng y = - \frac{1}{2}x, ta có h'(x) = 0 \Leftrightarrow x \in \left\{ - 2;0;4 ight\}

    Suy ra bảng biến thiên của hàm số h(x) như sau:

    Từ đó ta có bảng biến thiên của hàm số g(x) = \left| h(x) ight| như sau:

    Dựa vào bảng biến thiên trên, ta thấy hàm số g(x) đồng biến trên khoảng (0;4).

  • Câu 32: Vận dụng

    Tìm tổng các đường tiệm cận

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = \frac{1}{2f(x) - 1} là:

    Điều kiện xác định của hàm số y = \frac{1}{2f(x) - 1}là 2f(x) - 1 eq 0 \Leftrightarrow f(x) eq \frac{1}{2}

    Từ bảng biến thiên ta có: f(x) = \frac{1}{2} \Leftrightarrow \left\lbrack \begin{matrix} x = x_{1} \in ( - \infty; - 0,5) \\ x = x_{2} \in ( - 0,5; - \infty) \\ \end{matrix} ight.

    Tập xác định \mathbb{R}\backslash\left\{ x_{1};x_{2} ight\}

    Ta có:

    \lim_{x ightarrow - \infty}\frac{1}{2f(x) - 1} = \frac{1}{2.1 - 1} = 1 suy ra đồ thị hàm số có tiệm cận ngang y = 1.

    \lim_{x ightarrow + \infty}\frac{1}{2f(x) - 1} = \frac{1}{2.1 - 1} = 1 suy ra đồ thị hàm số có tiệm cận ngang y = 1.

    \lim_{x ightarrow {x_{1}}^{\pm}}\frac{1}{2f(x) - 1} = \mp \infty suy ra đồ thị hàm số có tiệm cận đứng x = x_{1}.

    \lim_{x ightarrow {x_{2}}^{\pm}}\frac{1}{2f(x) - 1} = \pm \infty suy ra đồ thị hàm số có tiệm cận đứng x = x_{2}.

    Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = \frac{1}{2f(x) - 1} là 3.

  • Câu 33: Thông hiểu

    Chọn đáp án đúng

    Cho hàm số y = f(x) liên tục trên \mathbb{R}\backslash\left\{ 1 \right\} có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = f(x)

    Do \lim_{x ightarrow 1^{+}}y = - \infty;\ \lim_{x ightarrow 1^{-}} = + \infty \Rightarrow TCĐ: x = 1.

    \lim_{x ightarrow + \infty}y = - 1;\ \lim_{x ightarrow - \infty}y = 1 \Rightarrowđồ thị có 2 tiệm cận ngang là y = \pm 1

    Vậy, đồ thị hàm số đã cho có tổng số TCĐ và TCN là 3.

  • Câu 34: Nhận biết

    Xác định tiệm cận ngang của đồ thị hàm số

    Tiệm cận ngang của đồ thị hàm số y = \frac{x - 2}{x + 1} là

    Ta thấy \left\{ \begin{gathered} \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 2}}{{x + 1}} = 1 \hfill \\ \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 2}}{{x + 1}} = 1 \hfill \\ \end{gathered} ight.

    Do đó đồ thị hàm số có tiệm cận ngang là y = 1.

  • Câu 35: Vận dụng

    Tìm giá trị của V

    Một khối gỗ có dạng hình khối nón có bán kính đáy bằng r = 2m, chiều cao h = 6m. Bác thợ mộc chế tác từ khúc gỗ thành một khúc gỗ có dạng hình khối trụ như hình vẽ:

    Gọi V là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Xác định giá trị của V

    Gọi r_{t};h_{t} lần lượt là bán kính và chiều cao của khối trụ.

    Ta có: \frac{r_{t}}{2} = \frac{6 - h_{t}}{6} \Rightarrow 2\left( 6 - h_{t} ight) = 6r_{t} \Leftrightarrow h_{t} = 6 - 3r_{t}

    Ta lại có: V = \pi{r_{t}}^{2}.h_{t} = \pi{r_{t}}^{2}.\left( 6 - 3r_{t} ight) = \pi.\left( 6{r_{t}}^{2} - 3{r_{t}}^{3} ight)

    Xét hàm số f\left( r_{t} ight) = 6{r_{t}}^{2} - 3{r_{t}}^{3} với r_{t} \in (0;2)có:

    f'\left( r_{t} ight) = 12r_{t} - 9{r_{t}}^{2}

    f'\left( r_{t} ight) = 0 \Leftrightarrow 12r_{t} - 9{r_{t}}^{2} = 0 \Leftrightarrow r_{t} = \frac{4}{3}

    Ta có bảng biến thiên như sau:

    Dựa vào bảng biến thiên ta có \max f\left( r_{t} ight) = \frac{32}{9} đạt tại r_{t} = \frac{4}{3}

    Vậy V = \frac{32\pi}{9}\left( m^{3} ight) là giá trị cần tìm.

  • Câu 36: Nhận biết

    Chọn kết luận đúng

    Hàm số y = f(x) có đạo hàm f'(x) > 0;\forall x\mathbb{\in R}. Kết luận nào sau đây đúng?

    Vì hàm số y = f(x) có đạo hàm f'(x) > 0;\forall x\mathbb{\in R} nên hàm số đồng biến trên \mathbb{R}.

  • Câu 37: Thông hiểu

    Ghi đáp án vào ô trống

    Cho hàm số y = f(x) có đạo hàm f'(x) = (x - 2)^{2019}\left( x^{2} - x -2 ight)^{2020}(x + 3)^{3}. Hỏi hàm số y = f\left( |x| ight) có bao nhiêu cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) có đạo hàm f'(x) = (x - 2)^{2019}\left( x^{2} - x -2 ight)^{2020}(x + 3)^{3}. Hỏi hàm số y = f\left( |x| ight) có bao nhiêu cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 38: Thông hiểu

    Chọn đáp án đúng

    Tìm tất cả các giá trị của tham số thực m để hàm số y = mx^{3} + mx^{2} + m(m - 1)x + 2 đồng biến trên \mathbb{R}.

    TH1: m = 0 \Rightarrow y = 2 là hàm hằng nên loại m = 0.

    TH2: m eq 0. Ta có: y' = 3mx^{2} + 2mx + m(m - 1).

    Hàm số đồng biến trên \mathbb{R \Leftrightarrow}f'(x) \geq 0\ \forall x\mathbb{\in R \Leftrightarrow}

    \left\{ \begin{matrix} \Delta' = m^{2} - 3m^{2}(m - 1) \leq 0 \\ 3m > 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m^{2}(4 - 3m) \leq 0 \\ m > 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m \geq \frac{4}{3} \\ m > 0 \\ \end{matrix} ight.\ \Leftrightarrow m \geq \frac{4}{3}

  • Câu 39: Nhận biết

    Tìm giá trị lớn nhất của hàm số

    Tìm giá trị lớn nhất của hàm số f(x) = x^{4} - 2x^{2} + 5 trên đoạn \lbrack - 2;2brack.

    Đạo hàm f'(x) = 4x^3 -4x

    \Rightarrow f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \in \lbrack - 2;2brack \\ x = 1 \in \lbrack - 2;2brack \\ x = - 1 \in \lbrack - 2;2brack \\ \end{matrix} ight.

    Ta có \left\{ \begin{matrix} f( - 2) = f(2) = 13 \\ f( - 1) = f(1) = 4 \\ f(0) = 5 \\ \end{matrix} ight.\ \Rightarrow \max_{\lbrack - 2;2brack}f(x) = 13

  • Câu 40: Thông hiểu

    Chọn đáp án đúng

    Hàm số y = \left| x^{3} + 3x^{2} ight| đạt cực đại tại

    Tập xác định: D\mathbb{= R}

    Ta có: y = \left| x^{3} + 3x^{2} ight| = \left\{ \begin{matrix} x^{3} + 3x^{2}\ \ khi\ x \geq - 3 \\ - x^{3} - 3x^{2}\ \ khi\ x < - 3 \\ \end{matrix} ight.

    \Rightarrow y' = \left\{ \begin{matrix} 3x^{2} + 6x\ \ khi\ x \geq - 3 \\ - 3x^{2} - 6x\ khi\ x < - 3 \\ \end{matrix} ight.

    \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} ight.

    Ta có bảng biến thiên

    Vậy hàm số đạt cực tiểu tại x = - 3 và x = 0.

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
25 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề kiểm tra 45 phút Chương 1 Ứng dụng đạo hàm để khảo sát hàm số CTST
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 12 - Chân trời sáng tạo
Xem thêm