Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Khóa học Lớp 12 Toán 12 - Chân trời sáng tạo
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề kiểm tra 45 phút Chương 6 Xác suất có điều kiện CTST

Mô tả thêm:

Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 6: Xác suất có điều kiện Toán 12 sách Chân trời sáng tạo các em nhé!
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Vận dụng

    Tính xác suất có điều kiện

    Trong một kỳ thi, có 60% học sinh đã làm đúng bài toán đầu tiên và 40% học sinh đã làm đúng bài toán thứ hai. Biết rằng có 20% học sinh làm đúng cả hai bài toán. Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là bao nhiêu?

    Ta có:

    A: "học sinh đã làm đúng bài toán đầu tiên", thì P(A) = 60\% = 0,6.

    B: "học sinh đã làm đúng bài toán thứ hai", thì P(B) = 40\% = 0,4.

    A \cap B: "học sinh làm đúng cả hai bài toán", thì P(A \cap B) = 20\% = 0,2.

    Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là P\left( B|A \right) = \frac{P(A \cap B)}{P(A)} = \frac{0,2}{0,6} = \frac{1}{3} \approx 0.33.

  • Câu 2: Thông hiểu

    Tính xác suất thắng thầu

    Một công ty xây dựng đấu thầu 2 dự án độc lập. Khả năng thắng thầu của các dự án 1 là 0,6 và dự án 2 là 0,7. Biết công ty thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2?

    Gọi A là biến cố ”Thắng thầu dự án 1″

    Gọi B là biến cố “Thắng thầu dự án 2″

    Theo đề bài ta có: \left\{ \begin{matrix} P(A) = 0,6 \Rightarrow P\left( \overline{A} ight) = 0,4 \\ P(B) = 0,3 \Rightarrow P\left( \overline{B} ight) = 0,7 \\ \end{matrix} ight. với 2 biến cố A; B độc lập.

    Gọi D là biến cố “thắng thầu dự án thứ 2 biết thắng thầu dự án 1” do A; B là hai biến cố độc lập nên:

    P(D) = P\left( B|A ight) = P(B) = 0,7

  • Câu 3: Nhận biết

    Kết luận đúng

    Giả sử A và B là hai biến cố ngẫu nhiên thỏa mãn P(A) > 0 và 0 < P(B) < 1. Khi đó

    Ta có: P\left( \left. \ B \right|A \right) = \frac{P(B)P\left( \left. \ A \right|B \right)}{P(B)P\left( \left. \ A \right|B \right) + P\left( \overline{B} \right)P\left( \left. \ A \right|\overline{B} \right)}

  • Câu 4: Thông hiểu

    Chọn đáp án đúng

    Có hai chiếc hộp đựng 30 chiếc bút chì có hình dáng, kích thước giống nhau. Sau khi thống kê nhận được bảng số liệu sau:

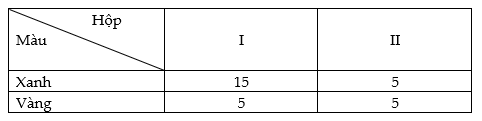
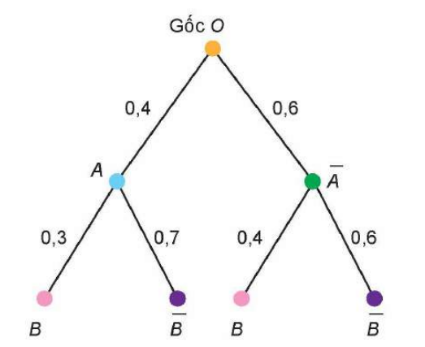
    Lấy ngẫu nhiên một chiếc bút từ hộp I bỏ sang hộp II. Sau đó, lấy ngẫu nhiên một chiếc bút từ hộp II. Xác suất để chiếc bút lấy ra từ hộp II có màu xanh là

    Gọi hai biến cố:

    A: “Lấy được bút xanh từ hộp I”;

    B: “Lấy được bút xanh từ hộp II”.

    Theo bài ra, ta có

    P(A) = \frac{15}{20} = \frac{3}{4} ; P\left( \overline{A} \right) = 1 - \frac{3}{4} = \frac{1}{4} ; P\left( B|A \right) = \frac{6}{11} ; P\left( B|\overline{A} \right) = \frac{5}{11}.

    Áp dụng công thức xác suất toàn phần, ta có

    P(B) = P(A)P\left( B|A \right) + P\left(\overline{A} \right)P\left( B|\overline{A} \right)=\frac{3}{4}.\frac{6}{11} + \frac{1}{4}.\frac{5}{11} =\frac{23}{44}.

  • Câu 5: Thông hiểu

    Tính xác suất lấy hai bi trắng

    Một hộp có 4 viên bi, mỗi viên có thể là màu đen hoặc trắng. Lấy ngẫu nhiên ra hai viên bi. Tính xác suất để lấy được hai bi trắng.

    Số lượng bi trắng và đen trong hộp chỉ có thể xảy ra 1 trong 5 trường hợp sau:

    H4: 4 bi trắng \Rightarrow P\left( H_{4} ight) = \frac{1}{5} = 0,2

    H3: 3 bi trắng; 1 bi đen \Rightarrow P\left( H_{3} ight) = \frac{1}{5} = 0,2

    H2: 2 bi trắng; 2 bi đen \Rightarrow P\left( H_{2} ight) = \frac{1}{5} = 0,2

    H1: 1 bi trắng; 3 bi đen \Rightarrow P\left( H_{1} ight) = \frac{1}{5} = 0,2

    H0: 0 bi trắng; 4 bi đen \Rightarrow P\left( H_{0} ight) = \frac{1}{5} = 0,2

    Gọi biến cố A là biến cố lấy được 2 bi trắng

    Ta có: \left\{ \begin{matrix}P\left( A|H_{4} ight) = 1;P\left( A|H_{3} ight) =\dfrac{C_{3}^{2}}{C_{4}^{2}} = \dfrac{1}{2} \\P\left( A|H_{2} ight) = \dfrac{C_{2}^{2}}{C_{4}^{2}} = \dfrac{1}{6} \\P\left( A|H_{1} ight) = 0;P\left( A|H_{0} ight) = 0 \\\end{matrix} ight.

    P(A) = P\left( H_{0} ight).P\left( A|H_{0} ight) + P\left( H_{1} ight)P\left( A|H_{1} ight) + P\left( H_{2} ight)P\left( A|H_{2} ight)

    + P\left( H_{3} ight)P\left( A|H_{3} ight) + P\left( H_{4} ight)P\left( A|H_{4} ight)

    \Rightarrow P(A) = 0,2.0 + 0,2.0 + 0,2.\frac{1}{6} + 0,2.\frac{1}{2} + 0,2.1 = \frac{1}{3}

  • Câu 6: Vận dụng cao

    Tính xác suất để cuộc gọi là đúng

    Một ứng dụng được sử dụng để chặn cuộc gọi rác trong điện thoại. Tuy nhiên, vì ứng dụng không tuyệt đối hoàn hảo nên một cuộc gọi rác bị chặn với xác suất 0,8 và một cuộc gọi đúng (không phải là cuộc gọi rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ cuộc gọi rác là 10\%. Chọn ngẫu nhiên một cuộc gọi không bị chặn. Xác suất để đó là cuộc gọi đúng là

    Gọi A là biến cố: “cuộc gọi được chọn là cuộc gọi rác”, B là biến cố: “cuộc gọi được chọn bị chặn” thì \overline{B} là biến cố: “cuộc gọi được chọn không bị chặn”.

    Theo đầu bài ta có: P(A) = 0,1; P\left( \overline{A} \right) = 0,9; P\left( \left. \ B \right|A \right) = 0,8; P\left( \left. \ B \right|\overline{A} \right) = 0,01.

    Ta có:

    P(B) = P\left( \left. \ B \right|A \right).P(A) + P\left( \left. \ B \right|\overline{A} \right).P\left( \overline{A} \right)

    = 0,8.0,1 + 0,01.0,9 = 0,089.

    Vì P\left( \left. \ B \right|\overline{A} \right) = 0,01 \Rightarrow P\left( \left. \ \overline{B} \right|\overline{A} \right) = 0,99

    P\left( \left. \ B \right|A \right) = 0,8 \Rightarrow P\left( \left. \ \overline{B} \right|A \right) = 0,2

    Theo công thức Bayes ta có:

    P\left( \left. \ \overline{A} \right|\overline{B} \right) = \frac{P\left( \overline{A} \right).P\left( \left. \ \overline{B} \right|\overline{A} \right)}{P\left( \overline{A} \right).P\left( \left. \ \overline{B} \right|\overline{A} \right) + P(A).P\left( \left. \ \overline{B} \right|A \right)}

    = \frac{0,9.0,99}{0,9.0,99 + 0,1.0,2} = \frac{891}{911}.

  • Câu 7: Nhận biết

    Tính P(A|B)

    Cho hai biến cố A và B, với P(A) = 0,2, P(B) = 0,26, P\left( B|A \right) = 0,7. Tính P\left( A|B \right).

    Theo công thức Bayes, ta có

    P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(B)} = \frac{0,2.0,7}{0,26} = \frac{7}{13}.

  • Câu 8: Nhận biết

    Tính xác suất

    Nếu hai biến cố A;B thỏa mãn P(A) = 0,3;P(B) = 0,6;P\left( A|B ight) = 0,4 thì P\left( B|A ight) bằng bao nhiêu?

    Theo công thức Bayes ta có:

    P\left( B|A ight) = \frac{P(B).P\left( A|B ight)}{P(A)}

    \Rightarrow P\left( B|A ight) = \frac{0,6.0,4}{0,3} = \frac{4}{5}

  • Câu 9: Nhận biết

    Tính xác suất P(A|B)

    Gieo con xúc xắc 1 lần. Gọi A là biến cố xuất hiện mặt 2 chấm. B là biến cố xuất hiện mặt chẵn. Xác suất P\left( A|B \right) là

    Theo định nghĩa xác suất có điều kiện ta có: P\left( A|B \right) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{1}{6}}{\frac{3}{6}} = \frac{1}{3}

  • Câu 10: Nhận biết

    Xác định P(A|B)

    Cho hai biến cố A,B có xác suất Ρ(A) = 0,4;Ρ(B) = 0,6;Ρ(AB) = 0,2. Tính xác suất Ρ\left( A|B \right).

    Theo định nghĩa xác suất có điều kiện, ta có Ρ\left( A|B \right) = \frac{Ρ(AB)}{Ρ(B)} = \frac{0,2}{0,6} = \frac{1}{3}.

  • Câu 11: Thông hiểu

    Tính xác suất thu được tín hiệu

    Một trạm chỉ phát hai tín hiệu A và B với xác suất tương ứng 0,84 và 0,16. do có nhiễu trên đường truyền nên \frac{1}{6} tín hiệu A bị méo và thu được như tín hiệu B còn \frac{1}{8} tín hiệu B bị méo và thu được như A. Tìm xác suất thu được tín hiệu A?

    Gọi A, B lần lượt là "phát ra tín hiệu A, B".

    Khi đó A, B tạo thành hệ đầy đủ.

    P(A) = 0,84;P(B) = 0,16

    Gọi C là "thu được tín hiệu A".

    Khi đó: P\left( C|A ight) = \frac{5}{6};P\left( C|B ight) = \frac{1}{8}

    Áp dụng công thức xác suất toàn phần ta có:

    P(C) = P(A).P\left( C|A ight) + P(B).P\left( C|B ight)

    \Rightarrow P(C) = 0,84.\frac{5}{6} + 0,16.\frac{1}{8} = 0,72.

  • Câu 12: Thông hiểu

    Chọn kết quả đúng

    Một trạm chỉ phát hai tín hiệu A và B với xác suất tương ứng 0,84 và 0,16. do có nhiễu trên đường truyền nên \frac{1}{6} tín hiệu A bị méo và thu được như tín hiệu B còn \frac{1}{8} tín hiệu B bị méo và thu được như A. Tìm xác suất thu được tín hiệu A?

    Gọi A, B lần lượt là "phát ra tín hiệu A, B".

    Khi đó A, B tạo thành hệ đầy đủ.

    P(A) = 0,84;P(B) = 0,16

    Gọi C là "thu được tín hiệu A". Khi đó: P\left( C|A ight) = \frac{5}{6};P\left( C|B ight) = \frac{1}{8}

    Áp dụng công thức xác suất toàn phần ta có:

    P(C) = P(A).P\left( C|A ight) + P(B).P\left( C|B ight)

    \Rightarrow P(C) = 0,84.\frac{5}{6} + 0,16.\frac{1}{8} = 0,72.

    Ta cần tính P(A|C). Áp dụng công thức Bayes ta có:

    P\left( A|C ight) = \frac{P(A)P\left(C|A ight)}{P(C)} = \dfrac{0,84.\dfrac{5}{6}}{0,72} =\dfrac{35}{36}

  • Câu 13: Nhận biết

    Xác định câu đúng

    Chọn khẳng định đúng.

    Câu đúng là : « Với hai biến cố A,B mà P(A) > 0,P(B) > 0, ta có:

    P(B|A) = \frac{P(B).P(A|B)}{P(A)}”

  • Câu 14: Vận dụng

    Xét tính đúng sai của các nhận định

    Để nghiên cứu sự phát triển của một loại cây, người ta trồng hạt giống của loại cây đó trên hai lô đất thí nghiệm M, N khác nhau. Xác suất phát triển bình thường của cây đó trên các lô đất M và N lần lượt là 0,56 và 0,62. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng. Xét các biến cố:

    A: “Cây phát triển bình thường trên lô đất M”;

    B: “Cây phát triển bình thường trên lô đất N”.

    a) Các cặp biến cố \overline{A}và B, A và \overline{B} là độc lập. Đúng||Sai

    b) Hai biến cố C = \overline{A}\ \cap B và D = \ A \cap \overline{B} không là hai biến cố xung khắc. Sai||Đúng

    c) P(\overline{A}) = 0,56; P(\overline{B}) = 0,62. Sai||Đúng

    d) Xác suất để cây chỉ phát triển bình thường trên một lô đất là 0,4856. Đúng||Sai

    Đáp án là:

    Để nghiên cứu sự phát triển của một loại cây, người ta trồng hạt giống của loại cây đó trên hai lô đất thí nghiệm M, N khác nhau. Xác suất phát triển bình thường của cây đó trên các lô đất M và N lần lượt là 0,56 và 0,62. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng. Xét các biến cố:

    A: “Cây phát triển bình thường trên lô đất M”;

    B: “Cây phát triển bình thường trên lô đất N”.

    a) Các cặp biến cố \overline{A}và B, A và \overline{B} là độc lập. Đúng||Sai

    b) Hai biến cố C = \overline{A}\ \cap B và D = \ A \cap \overline{B} không là hai biến cố xung khắc. Sai||Đúng

    c) P(\overline{A}) = 0,56; P(\overline{B}) = 0,62. Sai||Đúng

    d) Xác suất để cây chỉ phát triển bình thường trên một lô đất là 0,4856. Đúng||Sai

    a) Do hai lô đất khác nhau. Nên các cặp biến cố \overline{A}và B, A và \overline{B} là độc lập. Suy ra đúng.

    b) Do C \cap D = \overline{A}\ \cap A\ \cap B \cap \overline{B} = \varnothing nên hai biến cố C, D xung khắc. Suy ra sai.

    c) Tacó: P(\overline{A}) = 1 – P(A) = 1 – 0,56 = 0,44;

    P(\overline{B}) = 1 – P(B) = l – 0,62 = 0,38. Suy ra sai.

    d) Xác suất để cây chỉ phát triển bình thường trên một lô đất là:

    P(C \cup D) = P(C) + P(D) = P\left( \overline{A}\ \right).P(B) + P(A).P\left( \overline{B} \right)

    = 0,44. 0,62 + 0,56.0,38 = 0,4856. Suy ra đúng.

  • Câu 15: Vận dụng

    Tính xác suất người được chọn mắc bệnh A

    Tỉ lệ người dân đã tiêm vắc xin phòng bệnh A ở một địa phương là 65\%. Trong số những người đã tiêm phòng, tỉ lệ mắc bệnh A là 5\%; trong số những người chưa tiêm, tỉ lệ mắc bệnh A là 17\%. Chọn ngẫu nhiên một người ở địa phương đó. Tính xác suất người được chọn mắc bệnh A.

    Gọi X là biến cố “Người dân được tiêm phòng bệnh A”

    Y là biến cố “Người dân mắc bệnh A”.

    Ta có P(X) = 0,65 \Rightarrow P\left( \overline{X} \right) = 0,35.

    Tỉ lệ mắc bệnh khi tiêm phòng là: P\left( Y|X \right) = 0,05.

    Tỉ lệ mắc bệnh khi chưa tiêm phòng là P\left( Y|\overline{X} \right) = 0,17.

    Xác suất người này mắc bệnh A là:

    P(Y) = P(X).P\left( Y|X \right) + P\left( \overline{X} \right).P\left( Y|\overline{X} \right)

    = 0,65.0,05 + 0,35.0,17 = 0,092

  • Câu 16: Thông hiểu

    Tính xác suất để Hà được chọn vào đội tuyển

    Để được chọn vào đội tuyển học sinh giỏi môn Toán cấp thành phố, mỗi thí sinh phải vượt qua hai vòng thi. Bạn Hà tham dự cuộc tuyển chọn này. Xác suất để Hà qua được vòng thứ nhất là 0,8. Nếu qua được vòng thứ nhất thì xác suất để Hà qua được vòng thứ hai là 0,7. Xác suất để bạn Hà được chọn vào đội tuyển này là

    Gọi A là biến cố: “Hà qua được vòng thứ nhất” và B là biến cố: “Hà qua được vòng thứ hai”. Khi đó biến cố: “Hà được chọn vào đội tuyển” là AB.

    Ta có P(AB) = P(A).P\left( B\left| A \right.\ \right) = 0,8.0,7 = 0,56.

  • Câu 17: Vận dụng

    Xét tính đúng sai của các khẳng định

    Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ còn lại là nam. Có 3 bạn tên Hiền, trong đó có 1 bạn nữ và 2 bạn nam. Thầy giáo gọi ngẫu nhiên 1 bạn lên bảng.

    a) Xác suất để có tên Hiền là \frac{1}{10}. Đúng||Sai

    b) Xác suất để có tên Hiền, nhưng với điều kiện bạn đó nữ là \frac{3}{17}. Sai||Đúng

    c) Xác suất để có tên Hiền, nhưng với điều kiện bạn đó nam là \frac{2}{13}. Đúng||Sai

    d) Nếu thầy giáo gọi 1 bạn có tên là Hiền lên bảng thì xác xuất để bạn đó là bạn nữ là \frac{3}{17}. Sai||Đúng

    Đáp án là:

    Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ còn lại là nam. Có 3 bạn tên Hiền, trong đó có 1 bạn nữ và 2 bạn nam. Thầy giáo gọi ngẫu nhiên 1 bạn lên bảng.

    a) Xác suất để có tên Hiền là \frac{1}{10}. Đúng||Sai

    b) Xác suất để có tên Hiền, nhưng với điều kiện bạn đó nữ là \frac{3}{17}. Sai||Đúng

    c) Xác suất để có tên Hiền, nhưng với điều kiện bạn đó nam là \frac{2}{13}. Đúng||Sai

    d) Nếu thầy giáo gọi 1 bạn có tên là Hiền lên bảng thì xác xuất để bạn đó là bạn nữ là \frac{3}{17}. Sai||Đúng

    a) Xác suất để thầy giáo gọi bạn đó lên bảng có tên Hiền là

    Gọi A là biến cố “tên là Hiền”

    Gọi B là biến cố “nữ”.

    Xác suất để học sinh được gọi có tên là Hiền là: P(A) = \frac{3}{30} = \frac{1}{10}

    b) Xác suất để thầy giáo gọi bạn đó lên bảng có tên Hiền, nhưng với điều kiện bạn đó nữ là P\left( A|B \right)

    Ta có:

    P(B) = \frac{17}{30} ; P(A \cap B) = \frac{1}{30}

    Do đó: P\left( A|B \right) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{1}{30}}{\frac{17}{30}} = \frac{1}{17}

    c) Gọi C là biến cố “nam”.

    Xác suất để thầy giáo gọi bạn đó lên bảng có tên Hiền, nhưng với điều kiện bạn đó nam làP\left( A|C \right)

    Ta có:

    P(C) = \frac{13}{30} ; P(A \cap C) = \frac{2}{30}

    Do đó: P\left( A|C \right) = \frac{P(A \cap C)}{P(C)} = \frac{\frac{2}{30}}{\frac{13}{30}} = \frac{2}{13}

    d) Nếu thầy giáo gọi 1 bạn có tên là Hiền lên bảng thì xác xuất để bạn đó là bạn nữ là P\left( B|A \right)

    P\left( B|A \right) = \frac{P(A \cap B)}{P(A)} = \frac{\frac{1}{30}}{\frac{3}{30}} = \frac{1}{3}

    Đáp án: a) Đ, b) S, c) Đ, d) S.

  • Câu 18: Nhận biết

    Tính xác suất của biến cố

    Cho hai biến cố A,B với P(A) = 0,6; P(B) = 0,8 và P(A \cap B) = 0,4. Tính xác suất của P(A|B).

    Xác suất của biến cố là:

    P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{0,4}{0,8} = 0,5.

  • Câu 19: Thông hiểu

    Tính xác suất để chọn thư rác

    Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ thư rác là 3\%. Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác (kết quả làm tròn đến hàng phần nghìn).

    Gọi A là biến cố: “Thư được chọn là thư rác”; B là biến cố: “Thư được chọn là bị chặn”.

    Ta có P(A) = 3\% = 0,03;

    P\left( \overline{A} \right) = 1 - P(A) = 1 - 0,03 = 0,97;

    P\left( B|A \right) = 0,95;\ \ \ P\left( B|\overline{A} \right) = 0,01.

    Công thức Bayes, ta có:

    P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(A).P\left( B|A \right) + P\left( \overline{A} \right).P\left( B|\overline{A} \right)}

    = \frac{0,03.0,95}{0,03.0,95 + 0,97.0,01}\approx 0,746.

  • Câu 20: Thông hiểu

    Ghi lời giải bài toán vào chỗ trống

    Một bình đựng 50 viên bi kích thước, chất liệu như nhau, trong đó có 30 viên bi xanh và 20 viên bi trắng. Lấy ngẫu nhiên ra một viên bi, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được một viên bi xanh ở lần thứ nhất và một viên bi trắng ở lần thứ hai?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Một bình đựng 50 viên bi kích thước, chất liệu như nhau, trong đó có 30 viên bi xanh và 20 viên bi trắng. Lấy ngẫu nhiên ra một viên bi, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được một viên bi xanh ở lần thứ nhất và một viên bi trắng ở lần thứ hai?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 21: Nhận biết

    Tính P(A|B)

    Cho hai biến cố A và B là hai biến cố độc lập, với P(A) = 0,2024, P(B) = 0,2025. Tính P\left( A|B \right).

    Ta có: A và B là hai biến cố độc lập nên: P\left( A|B \right) = P(A) = 0,2024

  • Câu 22: Vận dụng

    Tính xác suất có điều kiện P(B|A)

    Một hộp chứa 4 quả bóng được đánh số từ 1 đến 4. An lấy ngẫu nhiên một quả bóng, bỏ ra ngoài, rồi lấy tiếp một quả bóng nữa. Xét các biến cố:

    A: "Quả bóng lấy ra lần đầu có số chẵn"

    B: "Quả bóng lấy ra lần hai có số lẻ".

    Tính xác suất có điều kiện P\left( B|A \right).

    Xác định không gian mẫu Ω và các biến cố.

    \Omega\ = \ \begin{Bmatrix} (1,2),\ (1,3),\ (1,4),\ (2,1),\ (2,3),\ (2,4),\ (3,1), \\ \ (3,2),\ (3,4),\ (4,1),\ (4,2),\ (4,3) \\ \end{Bmatrix}

    A\ = \ \left\{ (2,1),\ (2,3),\ (2,4),\ (4,1),\ (4,2),\ (4,3) \right\}

    B\ = \ \left\{ (1,1),(2,1),(3,1),(4,1),(1,3),(2,3),(3,3),(4,3) \right\}

    A \cap B\ = \ \left\{ (2,1),\ (2,3),\ (4,1),\ (4,3) \right\}

    Ta có n(\Omega) = 12.

    n(A) = 6 ⇒ P(A) = \frac{6}{12} = \frac{1}{2}; n(A \cap B) = 4 ⇒ P(A \cap B) = \frac{4}{12} = \frac{1}{3}.

    Vậy P\left( B|A \right) = \frac{P(A \cap B)}{P(A)} = \frac{\frac{1}{3}}{\frac{1}{2}} = \frac{2}{3}.

  • Câu 23: Nhận biết

    Tính xác suất

    Cho hai biến cố A;B với P(A) = \frac{1}{3};P(B) = \frac{1}{2};P(A + B) = \frac{3}{4}. Tính P\left( \overline{A}B ight)?

    Ta có:

    P(A.B) = P(A) + P(B) - P(A + B) = \frac{1}{12}

    \Rightarrow P\left( \overline{A}B ight) = P(B) - P(AB) = \frac{5}{12}

  • Câu 24: Thông hiểu

    Chọn đáp án đúng

    Có hai hộp bên ngoài giống nhau:

    Hộp thứ nhất đựng 1 sản phẩm lỗi và 9 sản phẩm tốt.

    Hộp thứ hai đựng 2 sản phẩm lỗi và 8 sản phẩm tốt.

    Lấy ngẫu nhiên một hộp, sau đó lấy ngẫu nhiên một sản phẩm. Xác suất để được sản phẩm tốt là:

    Gọi A1 là biến cố lấy sản phẩm từ hộp thứ nhất.

    A2 là biến cố lấy sản phẩm từ hộp thứ hai.

    Vì chọn ngẫu nhiên nên P\left( A_{1} ight) = P\left( A_{2} ight) = \frac{1}{2}

    Gọi B là biến cố lấy được sản phẩm tốt ta có:

    P\left( B|A_{1} ight) = \frac{9}{10};P\left( B|A_{2} ight) = \frac{8}{10}

    Do đó:

    P(B) = P\left( A_{1} ight).P\left( B|A_{1} ight) + P\left( A_{2} ight).P\left( B|A_{2} ight)

    \Rightarrow P(B) = \frac{1}{2}.\frac{9}{10} + \frac{1}{2}.\frac{8}{10} = \frac{17}{20} = 0,85

  • Câu 25: Vận dụng cao

    Tính xác suất của biến cố

    Bạn Tuấn hằng ngày ăn sáng bằng xôi hoặc bún. Nếu hôm nay bạn ăn sáng bằng xôi thì xác suất để hôm sau bạn ăn sáng bằng bún là 0,7. Xét một tuần mà thứ ba bạn ăn sáng bằng xôi. Biết xác suất để thứ năm tuần đó, bạn Tuấn ăn sáng bằng bún là 0,63. Hỏi nếu hôm nay bạn ăn sáng bằng bún thì xác suất để hôm sau bạn ăn sáng bằng xôi là

    Giả sử nếu hôm nay bạn ăn sáng bằng bún thì xác suất để hôm sau bạn ăn sáng bằng xôi là x (x < 1).

    Gọi A là biến cố “Thứ tư, bạn Tuấn ăn sáng bằng bún”,

    B là biến cố “Thứ năm, bạn Tuấn ăn sáng bằng bún”, khi đó P(B) = 0,63

    Ta cần tính P\left(\overline{B}|A \right)

    Ta có thứ ba bạn Tuấn ăn sáng bằng xôi nên P(A) = 0,7, P\left( \overline{A} \right) = 1 - 0,7 = 0,3

    Vì nếu hôm nay bạn ăn sáng bằng bún thì xác suất để hôm sau bạn ăn sáng bằng xôi là x và ăn sáng bằng bún là 1 - x hay P\left( B|A \right) = 1 - x.

    Ta có P\left( B|\overline{A} \right) = 0,7

    Theo công thức xác suất toàn phần:

    P(B) = P(A).P\left( B|A \right) +P\left( \overline{A} \right).P\left( B|\overline{A}\right)

    \Rightarrow 0,63 = 0,7.(1 - x) + 0,3.0,7

    \Rightarrow x = 0,4

    Vậy nếu hôm nay bạn ăn sáng bằng bún thì xác suất để hôm sau bạn ăn sáng bằng xôi là 0,4.

  • Câu 26: Nhận biết

    Xét tính đúng sai của các kết luận

    Một két nước ngọt đựng 24 chai nước có khối lượng và hình thức bề ngoài như nhau, trong đó

    có 16 chai loại I và 8 chai loại II. Bác Tùng lần lượt lấy ra ngẫu nhiên hai chai (lấy không hoàn lại). Xét

    các biến cố: A:” lần thứ nhất lấy ra chai nước loại I”; B:”Lần thứ hai lấy ra chai nước loại I”.

    a)P\left( B|A \right) = \frac{16}{23}. Sai||Đúng

    b)P\left( B|A \right) = \frac{15}{23}. Sai||Đúng

    c)P\left( B|A \right) = \frac{8}{23}. Đúng||Sai

    d) P\left( B|A \right) = \frac{7}{23}. Đúng||Sai

    Đáp án là:

    Một két nước ngọt đựng 24 chai nước có khối lượng và hình thức bề ngoài như nhau, trong đó

    có 16 chai loại I và 8 chai loại II. Bác Tùng lần lượt lấy ra ngẫu nhiên hai chai (lấy không hoàn lại). Xét

    các biến cố: A:” lần thứ nhất lấy ra chai nước loại I”; B:”Lần thứ hai lấy ra chai nước loại I”.

    a)P\left( B|A \right) = \frac{16}{23}. Sai||Đúng

    b)P\left( B|A \right) = \frac{15}{23}. Sai||Đúng

    c)P\left( B|A \right) = \frac{8}{23}. Đúng||Sai

    d) P\left( B|A \right) = \frac{7}{23}. Đúng||Sai

    Ta có: P(A) = \frac{16}{24} = \frac{2}{3};P(\overline{A}) = \frac{8}{24} = \frac{1}{3}.

    Nếu lần thứ nhất lấy ra chai loại I thì két còn 23 chai nước, trong đó có 15 chai loại I, 8 chai loại II. Suy ra P(B \mid A) = \frac{15}{23}.

    Nếu lần thứ nhất lấy ra chai loại II thì két còn 23 chai nước, trong đó có 16 chai loại I, 7 chai loại II. Suy ra P(B \mid \overline{A}) = \frac{16}{23}.

    Theo công thức xác suất toàn phần, ta có:

    P(B) = P(A).P(B \mid A) + P(\overline{A}).P(B \mid \overline{A}) = \frac{2}{3} \cdot \frac{15}{23} + \frac{1}{3} \cdot \frac{16}{23} = \frac{2}{3}.

    Ta có: P(\overline{B} \mid A) = 1 - P(B \mid A) = 1 - \frac{15}{23} = \frac{8}{23};

    P(\overline{B} \mid \overline{A}) = 1 - P(B \mid \overline{A}) = 1 - \frac{16}{23} = \frac{7}{23}.

    Đáp án: a) S, b) S, c) Đ, d) Đ.

  • Câu 27: Nhận biết

    Tính P(A|B)

    Cho hai biến cố A và B là hai biến cố độc lập, với P(A) = 0,2024; P(B) = 0,2025.

    Tính P\left( A\left| B \right.\ \right).

    Ta có: A và B là hai biến cố độc lập nên: P\left( A\left| B \right.\ \right) = P(A) = 0,2024

  • Câu 28: Vận dụng cao

    Tính xác suất của biến cố

    Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1 đáp án đúng được 5 điểm và mỗi câu trả lời sai bị trừ đi 2 điểm. Một học sinh không học bài nên đánh hàng loạt một câu trả lời. Tìm xác suất để học sinh này nhận điểm dưới 1.

    Xác suất để học sinh trả lời đúng 1 câu là \frac{1}{4} và trả lời sai 1 câu là \frac{3}{4}.

    Gọi x là số câu trả lời đúng \Rightarrow 10 - x là số câu trả lời sai.

    Số điểm học sinh đạt được là: 5x - 2.(10 - x) = 7x - 20

    Học sinh nhận được điểm dưới 1 khi 7x - 20 < 1 \Leftrightarrow x < 3

    Mà x\mathbb{\in Z \Rightarrow}x \in \{ 0;1;2\}

    Gọi A_{i}(i = 0,1,2) là biến cố: "Học sinh trả lời đúng i câu"

    A là biến cố "Học sinh nhận điểm dưới 1"

    Suy ra A = A_{0} \cup A_{1} \cup A_{2} và P(A) = P\left( A_{0}ight) + P\left( A_{1} ight) + P\left( A_{2} ight)

    Mà P\left( A_{i} ight) = C_{10}^{i}.\left( \frac{1}{4} ight)^{i}.\left( \frac{3}{4} ight)^{10 - i} nên P(A) = \sum_{i = 0,}^{2}C_{10}^{i}.\left( \frac{1}{4} ight)^{i}.\left( \frac{3}{4} ight)^{10 - i} = 0,5256

  • Câu 29: Thông hiểu

    Ghi đáp án vào ô trống

    Lớp 12A có 25 học sinh nam và 15 học sinh nữ. Trong số đó có 16 bạn nam và 6 bạn nữ thích chơi thể thao. Chọn một bạn bất kì của lớp 12A. Tính xác suất để bạn đó thích chơi thể thao biết rằng bạn học sinh đó là nữ (làm tròn đến hàng phần chục).

    Đáp án: 0,4

    Đáp án là:

    Lớp 12A có 25 học sinh nam và 15 học sinh nữ. Trong số đó có 16 bạn nam và 6 bạn nữ thích chơi thể thao. Chọn một bạn bất kì của lớp 12A. Tính xác suất để bạn đó thích chơi thể thao biết rằng bạn học sinh đó là nữ (làm tròn đến hàng phần chục).

    Đáp án: 0,4

    Xét 2 biến cố sau:

    A: “Học sinh được chọn là nữ”

    B: “Học sinh được chọn thích chơi thể thao”

    Khi đó, xác suất để bạn đó thích chơi thể thao biết rằng bạn học sinh đó là nữ là xác suất có điều kiện P(B|A).

    Ta có n(\Omega) = 40;n(A) = 15;n(B) = 16 + 6 = 22

    Áp dụng công thức ta có: P(B|A) = \dfrac{P(AB)}{P(A)} = \dfrac{\dfrac{6}{40}}{\dfrac{15}{40}} = \dfrac{2}{5} = 0,4

  • Câu 30: Nhận biết

    Chọn phát biểu đúng

    Cho hai biến cố A, B với 0 < P(B) < 1. Phát biểu nào sau đây đúng?

    Theo công thức xác suất toàn phần, ta có:

    P(A) = P(B).P\left( A|B ight) + P\left( \overline{B} ight).P\left( A|\overline{B} ight).

  • Câu 31: Thông hiểu

    Tính xác suất có điều kiện

    Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 10, biết rằng có ít nhất một con đã ra mặt 5 chấm.

    Gọi A : "ít nhất một con đã ra mặt 5 chấm".

    Và B : "tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10 ".

    Ta có: P(A) = 1 - P\left( \overline{A} \right) = 1 - \left( \frac{5}{6} \right)^{2} = \frac{11}{36} .

    Biến cố B có các trường hợp (4;6),(6;4),(5;5),(5;6),(6;5),(6;6) .

    Biến cố A \cap B có 3 trường hợp xảy ra: (5;5),(5;6),(6;5) có xác suất là: P(A \cap B) = \frac{3}{36} .

    Vậy P(B \mid A) = \frac{P(A \cap B)}{P(A)} = \frac{\frac{3}{36}}{\frac{11}{36}} = \frac{3}{11} .

  • Câu 32: Thông hiểu

    Tính xác suất để viên bi được chọn màu đỏ

    Có hai chiếc hộp đựng 50 viên bi có kích thước và khối lượng như nhau. Sau khi thống kê nhận được bảng số liệu sau:

    Chọn ngẫu nhiên một hộp, sau đó lấy ra ngẫu nhiên một viên bi từ hộp được chọn. Xác suất để chọn được viên bi màu đỏ là

    Xét hai biến cố

    A: “Chọn được hộp I”;

    B: “Chọn được viên bi màu đỏ”

    P(A) = \frac{1}{2} ; P\left( \overline{A} \right) = \frac{1}{2} ; P\left( B|A \right) = \frac{20}{35} = \frac{4}{7} ; P\left( B|\overline{A} \right) = \frac{5}{15} = \frac{1}{3}.

    Áp dụng công thức xác suất toàn phần, ta có

    P(B) = P(A)P\left( B|A \right) + P\left(\overline{A} \right)P\left( B|\overline{A} \right)

    =\frac{1}{2}.\frac{4}{7} + \frac{1}{2}.\frac{1}{3} =\frac{19}{42}.

  • Câu 33: Vận dụng

    Ghi đáp án vào ô trống

    Một xí nghiệp mỗi ngày sản xuất ra 2000 sản phẩm trong đó có 39 sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra. Tính xác suất của biến cố: Sản phẩm lấy ra lần thứ hai bị lỗi (làm tròn kết quả đến hàng phần trăm).

    Đáp án: 0,02

    Đáp án là:

    Một xí nghiệp mỗi ngày sản xuất ra 2000 sản phẩm trong đó có 39 sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra. Tính xác suất của biến cố: Sản phẩm lấy ra lần thứ hai bị lỗi (làm tròn kết quả đến hàng phần trăm).

    Đáp án: 0,02

    Xét các biến cố:

    A_{1}: Sản phẩm lấy ra lần thứ nhất bị lỗi.

    Khi đó, ta có: P\left( A_{1} ight) = \frac{39}{2000}; P\left( \overline{A_{1}} ight) = \frac{1961}{2000}.

    A_{2}: Sản phẩm lấy ra lần thứ hai bị lỗi.

    Khi sản phẩm lấy ra lần thứ nhất bị lỗi thì còn 1999 sản phẩm và trong đó có 38 sản phẩm lỗi nên ta có:

    P\left( {{A_2}\left| {{A_1}} ight.} ight) = \frac{{38}}{{1999}}, suy ra P\left( \overline{A_{2}}\left| A_{1} ight.\ ight) = \frac{1961}{1999}.

    Khi sản phẩm lấy ra lần thứ nhất không bị lỗi thì còn 1999 sản phẩm trong đó có 39sản phẩm lỗi nên ta có:

    P\left( A_{2}\left| \overline{A_{1}} ight.\ ight) = \frac{39}{1999}, suy ra P\left( \overline{A_{2}}\left| \overline{A_{1}} ight.\ ight) = \frac{1960}{1999}.

    Khi đó, xác suất để sản phẩm lấy ra lần thứ hai bị lỗi là:

    P\left( A_{2} ight) = P\left( A_{2}\left| A_{1} ight.\ ight).P\left( A_{1} ight) + P\left( A_{2}\left| \overline{A_{1}} ight.\ ight).P\left( \overline{A_{1}} ight)

    = \frac{38}{1999}.\frac{39}{2000} + \frac{39}{1999}.\frac{1961}{2000} \approx 0,02.

    Đáp số: 0,02.

  • Câu 34: Nhận biết

    Chọn công thức đúng

    Cho hai biến cố A và B là hai biến cố ngẫu nhiên màP(A) > 0,P(B) > 0, công thức Bayes là:

    Ta có: P\left( B|A \right) = \frac{P(B).P\left( A|B \right)}{P(A)}.

  • Câu 35: Vận dụng

    Tính xác suất của biến cố

    Chọn ngẫu nhiên lần lượt các số a, b phân biệt thuộc tập hợp \left\{ 3^{k} \mid k \in N,1 \leq k \leq 10 ight\}. Tính xác suất để \log_{a}b là một số nguyên dương.

    Phép thử: "Chọn ngẫu nhiên lần lượt các số a, b phân biệt thuộc tập hợp \left\{ 3^{k} \mid k \in N,1 \leq k \leq 10 ight\}

    Biến cố A: "\log_{a}b là một số nguyên dương".

    \Rightarrow n_{\Omega} = 10.9 = 90

    + Giả sử a = 3^{k_{1}},b = 3^{k_{2}}\left( k_{1} eq k_{2} ight) \Rightarrow log_{a}b = log_{3^{k_{1}}}\left( 3^{k_{2}} ight) = \frac{k_{2}}{k_{1}} là một số nguyên dương

    k_{2}

    10

    9

    8

    7

    6

    5

    4

    3

    2
    k_{1} 1;2;5 1;3 1;2;4

    1

    		 1;2;3

    1

    1;2

    1

    1

    \Rightarrow n_{A} = 17 \Rightarrow P(A) = \frac{n_{A}}{n_{\Omega}} = \frac{17}{90}.

  • Câu 36: Nhận biết

    Chọn đáp án đúng

    Cho hai biến cố A và B với 0 < P(B) < 1. Khi đó

    Ta có: P(A) = P(B)P\left( \left. \ A \right|B \right) + P\left( \overline{B} \right)P\left( \left. \ A \right|\overline{B} \right)

  • Câu 37: Nhận biết

    Tìm không gian mẫu của phép thử

    Một hộp chứa bốn viên bi cùng loại ghi số lần lượt từ 1 đến 4. Bạn Mạnh lấy ra một cách ngẫu nhiên một viên bi, bỏ viên bi đó ra ngoài và lấy ra một cách ngẫu nhiên thêm một viên bi nữa. Không gian mẫu của phép thử đó là

    Không gian mẫu là:

    \Omega = \begin{Bmatrix} (1,2);\ \ (1,3);\ \ (1,4);\ \ (2,1);\ \ (2,3);\ \ (2,4);\ \ \\ (3,1);\ \ (3,2);\ \ (3,4);\ \ (4,1);\ \ (4,2);\ \ (4,3) \\ \end{Bmatrix},

  • Câu 38: Thông hiểu

    Chọn đáp án đúng

    Có hai hộp đựng bóng giống nhau (khác màu sắc):

    Hộp thứ chứa 10 quả bóng trong đó có 9 quả màu đen.

    Hộp thứ hai chứa 20 quả bóng trng đó có 18 quả màu đen,

    Từ hộp thứ nhất lấy ngẫu nhiên một quả bóng bỏ sang hộp thứ hai. Tìm xác suất để lấy ngẫu nhiên một quả bóng từ hộp thứ hai được quả màu đen?

    Gọi A là biến cố lấy được quả bóng màu đen từ hộp thứ hai.

    Biến cố A có thể xảy ra đòng thời với một trong hai biến cố sau đây tạo nên một nhóm đầy đủ các biến cố:

    H1 là biến cố quả bóng bỏ từ hộp thứ nhất sang hộp thứ hai là màu đen.

    H2 là biến cố quả bóng bỏ từ hộp thứ nhất sang hộp thứ hai không phải màu đen.

    Xác suất để từ hộp thứ nhất bỏ sang hộp thứ hai là quả bóng màu đen bằng: P\left( H_{1} ight) = \frac{9}{10}

    Xác suất để từ hộp thứ nhất bỏ sang hộp thứ hai không phải quả bóng màu đen bằng: P\left( H_{2} ight) = \frac{1}{10}

    Xác suất có điều kiện để từ hộp thứ hai lấy được quả bóng màu đen khi các giả thuyết H_{1};H_{2} xảy ra là:

    P\left( A|H_{1} ight) = \frac{19}{21};P\left( A|H_{2} ight) = \frac{18}{21} = \frac{6}{7}

    Do đó:

    P(A) = P\left( H_{1} ight).\left( A|H_{1} ight) + P\left( H_{2} ight)P\left( A|H_{2} ight)

    \Rightarrow P(A) = \frac{9}{10}.\frac{19}{21} + \frac{1}{10}.\frac{6}{7} = 0,9

  • Câu 39: Thông hiểu

    Chọn đáp án đúng

    Trong hộp có 3 viên bi màu trắng và 7 viên bi màu đỏ. Lấy lần lượt mỗi lần một viên theo cách lấy không trả lại. Xác suất để viên bi lấy lần thứ hai là màu đỏ nếu biết rằng viên bị lấy lần thứ nhất cũng là màu đỏ là:

    Gọi A là biến cố “viên bi lấy lần thứ nhất là màu đỏ”.

    Gọi B là biến cố “viên bi lấy lần thứ hai là màu đỏ”.

    Không gian mẫu n(Ω )= 10.9 cách chọn

    Lần thứ nhất lấy 1 viên bi màu đỏ có 7 cách chọn, lần thứ hai lấy 1 viên bi trong 9 viên còn lại có cách 9 chọn, do đó: P(A) = \frac{7.9}{9.10} = \frac{7}{10}

    Lần thứ nhất lấy 1 viên bi màu đỏ có 7 cách chọn, lần thứ hai lấy 1 viên bi màu đỏ trong 6 viên bi còn lại có 6 cách chọn, do đó: P(A \cap B) = \frac{7.6}{10.9} = \frac{7}{15}

    Vậy xác suất để viên bi lấy lần thứ hai là màu đỏ nếu biết rằng viên bị lấy lần thứ nhất cũng là màu đỏ: P\left(B|A ight) = \dfrac{P(A \cap B)}{P(A)} =\dfrac{\dfrac{7}{15}}{\dfrac{7}{10}} = \dfrac{2}{3}.

  • Câu 40: Vận dụng cao

    Chọn đáp án hợp nhất

    Có 3 cửa hàng I, II, III cùng kinh doanh sản phẩm Y, trong đó thị phần của cửa hàng I, III như nhau và gấp đôi thị phần của cửa hàng II. Tỉ lệ sản phẩm loại A trong 3 cửa hàng lần lượt là 70\%; 75\% ; 50\%. Một khách hàng chọn ngẫu nhiên 1 cửa hàng và tử đó mua một sản phẩm. Giả sử khách hàng đã mua được sản phẩm loại A, hỏi khả năng người ấy đã mua được ở cửa hàng nào là nhiều nhất?

    Gọi T: "Khách hàng mua được sản phẩm loại A"

    Ai: "Mua ở cửa hàng i"

    Ta có {A1, A2, A3} là một hệ đầy đủ các biến cố và xác định được:P\left( A_{1} ight) = \frac{2}{5} = 0,4;P\left( A_{2} ight) = \frac{1}{5} = 0,2;P\left( A_{3} ight) = \frac{2}{5} = 0,4

    P\left( T|A_{1} ight) = 0,7;P\left( A|A_{2} ight) = 0,75;P\left( T|A_{3} ight) = 0,5

    Áp dụng công thức xác suất toàn phần ta có xác suất để khách hàng mua được sản phẩm loại A là:

    P(T) = P\left( A_{1} ight)P\left( T|A_{1} ight) + P\left( A_{2} ight)P\left( A|A_{2} ight) + P\left( A_{3} ight)P\left( T|A_{3} ight)

    \Rightarrow P(T) = 0,4.0,7 + 0,2.0,75 + 0,4.0,5 = 0,63

    Áp dụng công thức Bayes, ta có:

    P\left( A_{1}|T ight) = \frac{P\left( A_{1} ight)P\left( T|A_{1} ight)}{P(T)} = \frac{0,4.0,7}{0,63} = 0,4444

    P\left( A_{21}|T ight) = \frac{P\left( A_{2} ight)P\left( T|A_{2} ight)}{P(T)} = \frac{0,2.0,75}{0,63} = 0,2381

    P\left( A_{3}|T ight) = \frac{P\left( A_{3} ight)P\left( T|A_{3} ight)}{P(T)} = \frac{0,4.0,5}{0,63} = 0,3175

    Ta thấy rằng P(A1|T) là lớn nhất tức là khả năng người ấy đã mua ở cửa hàng I là nhiều nhất.

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 6 Xác suất có điều kiện CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
42 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề kiểm tra 45 phút Chương 6 Xác suất có điều kiện CTST
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 12 - Chân trời sáng tạo
Xem thêm