A.B.C.D.ĐÚNGĐÚNGSAISAI
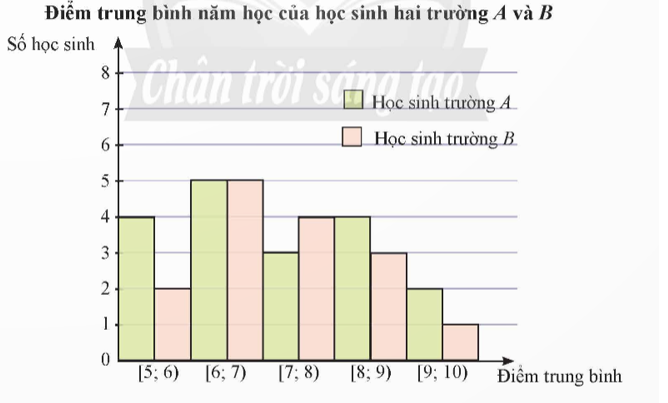
a) Giá trị đại diện của nhóm [5; 6) là 5,5.
Giá trị đại diện của nhóm [6; 7) là 6,5.
Giá trị đại diện của nhóm [7; 8) là 7,5.
Giá trị đại diện của nhóm [8; 9) là 8,5.
Giá trị đại diện của nhóm [9; 10) là 9,5.
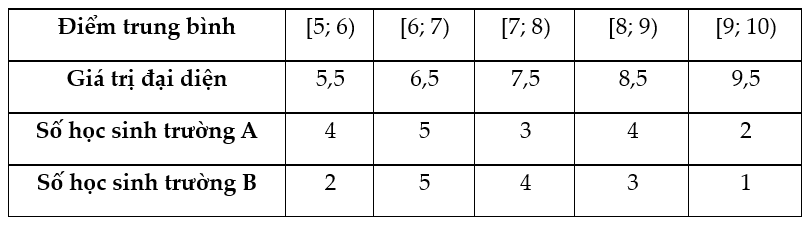
Từ biểu đồ, ta có bảng tần số ghép nhóm sau:
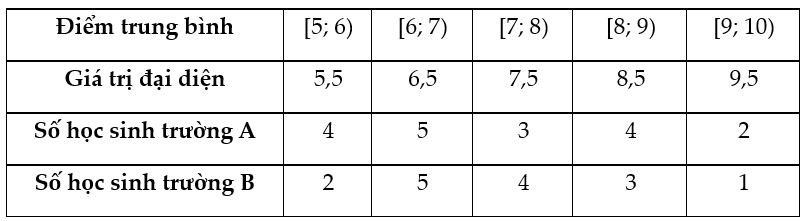
b) Xét mẫu số liệu của trường A:
Cỡ mẫu nA = 4 + 5 + 3 + 4 + 2 = 18.
Gọi  là mẫu số liệu gốc về điểm trung bình năm học của học sinh trường A được xếp theo thứ tự không giảm.
là mẫu số liệu gốc về điểm trung bình năm học của học sinh trường A được xếp theo thứ tự không giảm.
Ta có
 [5; 6),
[5; 6),
 [6; 7),
[6; 7),
 [7; 8),
[7; 8),
 [8; 9),
[8; 9),
 [9; 10).
[9; 10).
Tứ phân vị thứ nhất của mẫu số liệu gốc là  [6; 7). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
[6; 7). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: %20%3D%206%2C1)
Tứ phân vị thứ ba của mẫu số liệu gốc là  [8; 9). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
[8; 9). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: %7D%7B4%7D(9%20-%208)%20%3D%208%2C375)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: ∆Q = Q3 – Q1 = 8,375 – 6,1 = 2,275.
Xét mẫu số liệu của trường B:
Cỡ mẫu nB = 2 + 5 + 4 + 3 + 1 = 15.
Gọi  là mẫu số liệu gốc về điểm trung bình năm học của học sinh trường B được xếp theo thứ tự không giảm.
là mẫu số liệu gốc về điểm trung bình năm học của học sinh trường B được xếp theo thứ tự không giảm.
Ta có
 [5; 6),
[5; 6),
 [6; 7),
[6; 7),
 [7; 8),
[7; 8),
 [8; 9),
[8; 9),
 [9; 10).
[9; 10).
Tứ phân vị thứ nhất của mẫu số liệu gốc là  [6; 7). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
[6; 7). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: %20%3D%206%2C35)
Tứ phân vị thứ ba của mẫu số liệu gốc là  [8; 9). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
[8; 9). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: %7D%7B3%7D(9%20-%208)%20%3D%0A%5Cfrac%7B97%7D%7B12%7D)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 
d) Vì ∆Q = 2,275 > ∆'Q ≈ 1,73 nên nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn.