Xác định tọa độ điểm C
Trong không gian ![]() , cho hình bình hành hình bình hành. Biết các điểm
, cho hình bình hành hình bình hành. Biết các điểm ![]() . Xác định tọa độ điểm
. Xác định tọa độ điểm ![]() ?
?
Giả sử điểm ta có
là hình bình hành nên
. Vậy tọa độ điểm
.
Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 2: Vectơ và hệ tọa độ trong không gian Toán 12 sách Chân trời sáng tạo các em nhé!
Xác định tọa độ điểm C
Trong không gian ![]() , cho hình bình hành hình bình hành. Biết các điểm
, cho hình bình hành hình bình hành. Biết các điểm ![]() . Xác định tọa độ điểm
. Xác định tọa độ điểm ![]() ?
?
Giả sử điểm ta có
là hình bình hành nên
. Vậy tọa độ điểm
.
Xác định tọa độ điểm C’
Trong không gian hệ trục tọa độ ![]() , cho hình hộp
, cho hình hộp ![]() có tọa độ các điểm
có tọa độ các điểm ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() ?
?
Theo quy tắc hình hộp ta có:
Lại có
mà
Suy ra
Tìm m thỏa mãn điều kiện
Trong không gian ![]() cho
cho ![]() véc tơ
véc tơ ![]() ;
; ![]() . Tìm
. Tìm ![]() để
để ![]() .
.
Ta có:
.
Tìm tọa độ điểm D
Trong không gian ![]() , cho các điểm
, cho các điểm ![]() . Xác định tọa độ điểm
. Xác định tọa độ điểm ![]() sao cho tứ giác
sao cho tứ giác ![]() là hình bình hành?
là hình bình hành?
Giả sử điểm ta có
là hình bình hành nên
. Vậy tọa độ điểm
.
Ghi đáp án đúng vào ô trống
ột nguồn âm phát ra sóng âm là sóng cầu. Khi gắn hệ trục toạ độ ![]() (đơn vị trên mỗi trục là mét). Cường độ âm chuẩn tại điểm
(đơn vị trên mỗi trục là mét). Cường độ âm chuẩn tại điểm ![]() là tâm của nguồn phát âm với bán kính
là tâm của nguồn phát âm với bán kính ![]() . Để kiểm tra một điểm ở vị trí
. Để kiểm tra một điểm ở vị trí![]() có nhận được cường độ âm phát ra tại
có nhận được cường độ âm phát ra tại ![]() hay không người ta sẽ tính khoảng cách giữa hai vị trí
hay không người ta sẽ tính khoảng cách giữa hai vị trí ![]() và
và ![]() . Hỏi khoảng cách giữa hai vị trí
. Hỏi khoảng cách giữa hai vị trí ![]() và
và ![]() là bao nhiêu mét?
là bao nhiêu mét?
Đáp án: 14 (m)
ột nguồn âm phát ra sóng âm là sóng cầu. Khi gắn hệ trục toạ độ ![]() (đơn vị trên mỗi trục là mét). Cường độ âm chuẩn tại điểm
(đơn vị trên mỗi trục là mét). Cường độ âm chuẩn tại điểm ![]() là tâm của nguồn phát âm với bán kính
là tâm của nguồn phát âm với bán kính ![]() . Để kiểm tra một điểm ở vị trí
. Để kiểm tra một điểm ở vị trí![]() có nhận được cường độ âm phát ra tại
có nhận được cường độ âm phát ra tại ![]() hay không người ta sẽ tính khoảng cách giữa hai vị trí
hay không người ta sẽ tính khoảng cách giữa hai vị trí ![]() và
và ![]() . Hỏi khoảng cách giữa hai vị trí
. Hỏi khoảng cách giữa hai vị trí ![]() và
và ![]() là bao nhiêu mét?
là bao nhiêu mét?
Đáp án: 14 (m)
Ta có
(m).
Đáp số 14(m).
Tính giá trị của tham số k
Cho hình hộp ![]() . Tìm giá trị thực của
. Tìm giá trị thực của ![]() thỏa mãn đẳng thức vectơ
thỏa mãn đẳng thức vectơ ![]()
Hình vẽ minh họa
Ta có:
.
Vậy .
Chọn đáp án thích hợp
Trong không gian tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() sao cho
sao cho ![]() là trung điểm của
là trung điểm của ![]() ?
?
Gọi tọa độ điểm . Vì M là trung điểm của AB nên ta có:
Vậy tọa độ điểm B cần tìm là .
Tìm câu sai
Cho ![]() góc giữa hai vecto bằng
góc giữa hai vecto bằng ![]() . Tìm câu sai dưới đây?
. Tìm câu sai dưới đây?
Ta có:
Chọn mệnh đề sai
Trong không gian ![]() , cho tọa độ các vectơ
, cho tọa độ các vectơ ![]() ;
; ![]() và
và ![]() . Mệnh đề nào sau đây sai?
. Mệnh đề nào sau đây sai?
Ta có: suy ra “
” là mệnh đề sai.
Chọn đáp án thích hợp
Cho hình hộp ![]() . Gọi
. Gọi ![]() và
và ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Vectơ nào sau đây bằng
. Vectơ nào sau đây bằng ![]() ?
?

Ta có cùng hướng với
và
, suy ra
Xác định tọa độ điểm trong không gian
Trong không gian ![]() , điểm đối xứng của điểm
, điểm đối xứng của điểm ![]() qua trục
qua trục ![]() có tọa độ là
có tọa độ là
Gọi là điểm đối xứng của
qua trục
.
Hình chiếu vuông góc của lên trục
là
Khi đó là trung điểm của
. Do đó tọa độ của
là
Tìm tọa độ điểm M thỏa mãn yêu cầu
Trong không gian hệ trục tọa độ ![]() , cho ba điểm
, cho ba điểm ![]() . Tìm điểm
. Tìm điểm ![]() sao cho
sao cho ![]() đạt giá trị nhỏ nhất?
đạt giá trị nhỏ nhất?
Vì suy ra
. Ta có:
Theo bài ra:
Vậy nhỏ nhất bằng
khi
. Hay
Tìm tọa độ hình chiếu của M trên Ox
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Tìm tọa độ hình chiếu M lên trục
. Tìm tọa độ hình chiếu M lên trục ![]() .
.
Tọa độ hình chiếu của điểm M trên trục Ox là
Xác định tọa độ điểm M
Trong không gian với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Điểm
. Điểm ![]() thỏa mãn
thỏa mãn ![]() có tọa độ là:
có tọa độ là:
Từ giả thiết nên ba điểm
thẳng hàng và
nằm cùng phía so với điểm
do
dương.
Lại có
.
Vậy B là trung điểm của MA.
Khi đó ta đươc tọa độ điểm .
Tính góc giữa hai vectơ
Trong không gian ![]() , góc giữa hai vectơ
, góc giữa hai vectơ ![]() và
và ![]() là
là
Ta có .
Khi đó:
=.
Chọn phương án đúng
Cho hình chóp ![]() có
có ![]() là hình chữ nhật có
là hình chữ nhật có ![]() ,
, ![]() ; giá trị của
; giá trị của ![]() là
là
Vì
Xác định tham số m theo yêu cầu
Trong không gian ![]() , cho các vec tơ
, cho các vec tơ ![]() và
và ![]() . Có bao nhiêu giá trị nguyên dương của
. Có bao nhiêu giá trị nguyên dương của ![]() để góc giữa hai vec tơ
để góc giữa hai vec tơ ![]() và
và ![]() là góc tù?
là góc tù?
Ta có .
Góc giữa hai vec tơ và
là góc tù khi và chỉ khi
.
Vì nguyên dương nên
.
Vậy có 2 giá trị thỏa mãn yêu cầu bài toán.
Ghi đáp án vào ô trống
Một chiếc máy được đặt trên một giá đỡ ba chân tại điểm đặt ![]() , giá đỡ có các điểm tiếp xúc mặt đất của ba chân lần lượt là
, giá đỡ có các điểm tiếp xúc mặt đất của ba chân lần lượt là  ,
, . Biết rằng trọng lượng của chiếc máy là
. Biết rằng trọng lượng của chiếc máy là ![]() , tác dụng lên các giá đỡ theo các lực
, tác dụng lên các giá đỡ theo các lực ![]() như hình.
như hình.

Tính tích vô hướng của ![]() (làm tròn đến chữ số hàng đơn vị).
(làm tròn đến chữ số hàng đơn vị).
Đáp án: 6311
Một chiếc máy được đặt trên một giá đỡ ba chân tại điểm đặt ![]() , giá đỡ có các điểm tiếp xúc mặt đất của ba chân lần lượt là
, giá đỡ có các điểm tiếp xúc mặt đất của ba chân lần lượt là  ,
, . Biết rằng trọng lượng của chiếc máy là
. Biết rằng trọng lượng của chiếc máy là ![]() , tác dụng lên các giá đỡ theo các lực
, tác dụng lên các giá đỡ theo các lực ![]() như hình.
như hình.

Tính tích vô hướng của ![]() (làm tròn đến chữ số hàng đơn vị).
(làm tròn đến chữ số hàng đơn vị).
Đáp án: 6311
Ta có:
.
Suy ra, (vì chân bằng nhau, giá đỡ cân bằng, trọng lực tác dụng đều lên 3 chân của giá đỡ).
Do đó:
.
Mà .
Suy ra .
Từ đó .
Vậy .
Hoàn thành mệnh đề
Cho hai đường thẳng ![]() và
và ![]() lần lượt có vectơ chỉ phương là
lần lượt có vectơ chỉ phương là ![]() và
và ![]() . Nếu
. Nếu ![]() là góc giữa hai đường thẳng
là góc giữa hai đường thẳng ![]() và
và ![]() thì:
thì:
Do góc giữa hai đường thẳng bằng hoặc bù với góc giữa hai vectơ chỉ phương của chúng nên đáp án cần tìm là .
Chọn đáp án đúng
Cho tứ diện ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() . Tìm giá trị thực của
. Tìm giá trị thực của ![]() thỏa mãn đẳng thức vectơ
thỏa mãn đẳng thức vectơ ![]() ?
?
Hình vẽ minh họa
Ta có N là trung điểm của CD nên
M là trung điểm của AB nên
Suy ra
Ghi đáp án đúng vào ô trống
Cho tam giác ![]() có ba góc đều là góc nhọn. Gọi
có ba góc đều là góc nhọn. Gọi ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() ,
, ![]() là chân đường cao hạ từ
là chân đường cao hạ từ ![]() xuống cạnh
xuống cạnh ![]() thỏa mãn:
thỏa mãn: ![]() . Điểm
. Điểm ![]() đi động trên
đi động trên ![]() sao cho
sao cho ![]() (Trong đó
(Trong đó ![]() là phân số tối giản,
là phân số tối giản, ![]() ). Tính giá trị biểu thức
). Tính giá trị biểu thức ![]() khi độ dài véc tơ
khi độ dài véc tơ ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Đáp án: 9
Cho tam giác ![]() có ba góc đều là góc nhọn. Gọi
có ba góc đều là góc nhọn. Gọi ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() ,
, ![]() là chân đường cao hạ từ
là chân đường cao hạ từ ![]() xuống cạnh
xuống cạnh ![]() thỏa mãn:
thỏa mãn: ![]() . Điểm
. Điểm ![]() đi động trên
đi động trên ![]() sao cho
sao cho ![]() (Trong đó
(Trong đó ![]() là phân số tối giản,
là phân số tối giản, ![]() ). Tính giá trị biểu thức
). Tính giá trị biểu thức ![]() khi độ dài véc tơ
khi độ dài véc tơ ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Đáp án: 9
Hình vẽ minh họa
Gọi là trung điểm của
,
là điểm đối xứng của
qua
.
Khi đó tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên
là hình bình hành.
.
+ Dựng .
Ta có: .
Do đó nhỏ nhất khi
.
+ Ta có: .
+ Gọi là hình chiếu vuông góc của
lên
.
Ta có:
.
+ Do //
(vì cùng vuông góc với
).
Nên và
đồng dạng
.
+ có
là trung điểm
và
//
(do cùng vuông góc với
).
là đường trung bình.
Khi đó, là trung điểm
hay
.
Vậy .
Tìm tọa độ vectơ
Trong không gian với hệ trục tọa độ ![]() , cho hai vectơ
, cho hai vectơ ![]() . Tìm tọa độ vectơ
. Tìm tọa độ vectơ ![]() ?
?
Ta có: . Khi đó
.
Vậy
Chọn khẳng định đúng
Cho tứ diện ![]() . Gọi
. Gọi ![]() là các điểm thỏa nãm
là các điểm thỏa nãm ![]() còn
còn ![]() là các điểm xác định bởi
là các điểm xác định bởi ![]() . Chứng minh ba điểm
. Chứng minh ba điểm ![]() thẳng hàng. Khẳng định nào sau đây là đúng?
thẳng hàng. Khẳng định nào sau đây là đúng?
Hình vẽ minh họa
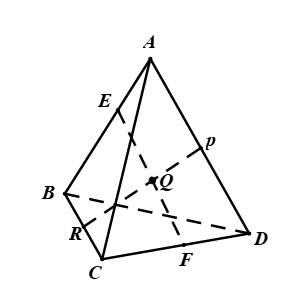
Ta có
Từ ta có
Lấy theo vế ta có
Tương tự
Mặt khác nên
Vậy thẳng hàng.
Tính góc giữa hai đường thẳng
Cho hình hộp ![]() có các cạnh đều bằng
có các cạnh đều bằng ![]() và các góc
và các góc ![]() . Tính diện tích các tứ giác
. Tính diện tích các tứ giác ![]() và
và ![]() .
.
Hình vẽ minh họa
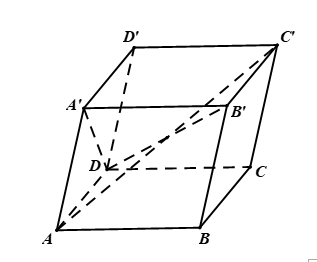
Ta có:
nên
.
Dễ dàng tính được
,
.
Tính được
Vậy .
Tìm tọa độ điểm B’
Trong không gian hệ trục tọa độ ![]() , cho hình hộp
, cho hình hộp ![]() . Biết
. Biết ![]() . Tọa độ điểm
. Tọa độ điểm ![]() là:
là:
Hình vẽ minh họa
Ta có:
Chọn khẳng định đúng
Trong không gian cho hình hộp ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Hình vẽ minh họa
Ta có: suy ra
đồng phẳng.
Tính giá trị của biểu thức
Trong không gian ![]() , cho
, cho ![]() , điểm
, điểm ![]()
![]() và
và
điểm ![]() sao cho
sao cho ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() . Khi đó
. Khi đó ![]() bằng
bằng
Ta có:
Tìm tọa độ trọng tâm tam giác
Cho tam giác ![]() có
có ![]() . Tọa độ của trọng tâm
. Tọa độ của trọng tâm ![]() của tam giác
của tam giác ![]() là:
là:
Với G là trọng tâm tam giác ABC:
Vậy tọa độ trọng tâm tam giác có tọa độ là .
Tìm tọa độ vecto
Trong không gian ![]() , cho
, cho ![]() . Tọa độ
. Tọa độ ![]() bằng?
bằng?
Ta có:
Chọn khẳng định đúng
Trong không gian ![]() , cho vectơ
, cho vectơ ![]() . Tọa độ điểm
. Tọa độ điểm ![]() là:
là:
Ta có:
Xác định vị trí điểm M
Cho tứ diện ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() ,
, ![]() là trung điểm của
là trung điểm của ![]() ). Xác định vị trí của
). Xác định vị trí của ![]() để
để ![]() nhỏ nhất.
nhỏ nhất.
Hình vẽ minh họa
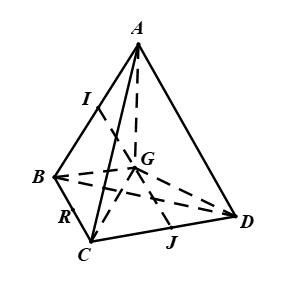
Ta có nên
nhỏ nhất khi
.
Chọn biểu thức phân tích vectơ đúng
Cho hình lăng trụ tam giác ![]() có
có ![]() . Hãy phân tích vectơ
. Hãy phân tích vectơ ![]() theo các vectơ
theo các vectơ ![]() ?
?
Hình vẽ minh họa
Ta có:
Chọn phương án thích hợp
Cho hình hộp ![]() . Trong các vectơ sau, vectơ nào bằng vectơ
. Trong các vectơ sau, vectơ nào bằng vectơ ![]() ?
?
Hình vẽ minh họa:
Đáp án cần tìm:
Chọn mệnh đề đúng
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Vì tọa độ điểm có
nên
.
Tìm vectơ cùng phương với vectơ đã cho
Trong không gian ![]() , cho vectơ
, cho vectơ ![]() . Hãy chọn vectơ cùng phương với
. Hãy chọn vectơ cùng phương với ![]() ?
?
Ta có: cùng phương với
khi
. Khi đó đáp án cần tìm là
(vì
).
Ghi đáp án vào ô trống
Trong không gian với hệ trục tọa độ ![]() cho hình thang
cho hình thang ![]() vuông tại
vuông tại ![]() và
và ![]() . Biết rằng tọa độ các điểm
. Biết rằng tọa độ các điểm ![]() và hình thang
và hình thang ![]() có diện tích bằng
có diện tích bằng ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Trong không gian với hệ trục tọa độ ![]() cho hình thang
cho hình thang ![]() vuông tại
vuông tại ![]() và
và ![]() . Biết rằng tọa độ các điểm
. Biết rằng tọa độ các điểm ![]() và hình thang
và hình thang ![]() có diện tích bằng
có diện tích bằng ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ghi đáp án đúng vào ô trống
Ba chiếc máy bay không người lái cùng bay lên từ một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Đông ![]() và về phía Nam
và về phía Nam ![]() , đồng thời cách mặt đất
, đồng thời cách mặt đất ![]() . Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc
. Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc ![]() và về phía Tây
và về phía Tây ![]() , đồng thời cách mặt đất
, đồng thời cách mặt đất ![]() . Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng.
. Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng.

Xác định khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó.
Đáp án: 20,8
Ba chiếc máy bay không người lái cùng bay lên từ một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Đông ![]() và về phía Nam
và về phía Nam ![]() , đồng thời cách mặt đất
, đồng thời cách mặt đất ![]() . Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc
. Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc ![]() và về phía Tây
và về phía Tây ![]() , đồng thời cách mặt đất
, đồng thời cách mặt đất ![]() . Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng.
. Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng.

Xác định khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó.
Đáp án: 20,8
Chọn hệ trục tọa độ , với gốc đặt tại điểm xuất phát của hai chiếc máy bay, mặt phẳng
trùng với mặt đất, trục
hướng về phía Bắc, trục
hướng về phía Tây, trục
hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét (xem hình vẽ).
Chiếc máy bay thứ nhất có tọa độ .
Chiếc máy bay thứ hai có tọa độ .
Do chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng nên ở vị trí trung điểm, suy ra chiếc máy bay thứ ba có tọa độ .
Khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó là:
.
Xác định tọa độ hình chiếu
Trong không gian tọa độ ![]() , hình chiếu vuông góc của điểm
, hình chiếu vuông góc của điểm ![]() trên mặt phẳng
trên mặt phẳng ![]() là:
là:
Hình chiếu vuông góc của điểm trên mặt phẳng
là điểm có tọa độ
.
Phân tích vectơ
Cho hình lập phương ![]() . Hãy phân tích vectơ
. Hãy phân tích vectơ ![]() theo các vectơ
theo các vectơ ![]() ?
?
Hình vẽ minh họa
Ta có: (Theo quy tắc hình bình hành).
Tìm câu sai
Cho hình hộp ![]() với tâm
với tâm ![]() .
.
Ta có mà
nên
sai.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
