VnDoc.com

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 89.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Đề kiểm tra 45 phút Chương 2 Vectơ và hệ trục tọa độ trong không gian

Mô tả thêm:

Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 2: Vectơ và hệ trục tọa độ trong không gian Toán 12 sách Kết nối tri thức các em nhé!

Thời gian làm: 45 phút
Số câu hỏi: 40 câu
Số điểm tối đa: 40 điểm
Tài khoản: Đăng nhập

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Rủ bạn học

Câu 1: Nhận biết
Xác định tọa độ vectơ

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{a} = (1;2;1);\overrightarrow{b} = ( - 1;3;0)$ . Vectơ $\overrightarrow{c} = 2\overrightarrow{a} + \overrightarrow{b}$ có tọa độ là:
- A.
  $\overrightarrow{c} = (1;7;2)$
- B.
  $\overrightarrow{c} = (1;5;2)$
- C.
  $\overrightarrow{c} = (3;7;2)$
- D.
  $\overrightarrow{c} = (1;7;3)$
Ta có: $2\overrightarrow{a} = (2;4;2)$ . Khi đó $\overrightarrow{c} = 2\overrightarrow{a} + \overrightarrow{b} = \left( 2 + ( - 1);4 + 3;2 + 0 ight) = (1;7;2)$

Vậy $\overrightarrow{c} = (1;7;2)$
Câu 2: Nhận biết
Chọn đáp án đúng

Trong không gian hệ trục tọa độ $Oxyz$ , điểm nào dưới đây thuộc trục $Oy$ ?
- A.
  $H(2;0;0)$
- B.
  $K(0;3;2)$
- C.
  $U(2;0;3)$
- D.
  $T(0; - 3;0)$
Điểm $A(x;y;z) \in Oy \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ z = 0 \\ \end{matrix} ight.$ . Suy ra trong bốn điểm đã cho điểm $T(0; - 3;0) \in Oy$ .
Câu 3: Vận dụng

Ghi đáp án vào chỗ trống

Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.
Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ $900(km/h)$ lên $920(km/h)$ , trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc $900(km/h)$ và $920(km/h)$ lần lượt biểu diễn bởi hai vectơ $\overrightarrow{F_{1}}$ và $\overrightarrow{F_{2}}$ với $\overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight)$ . Tính giá trị của $k$ (Làm tròn kết quả đến chữ số thập phân thứ hai).
Chỗ nhập nội dung câu trả lời tự luận

Đáp án là:

Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.
Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ $900(km/h)$ lên $920(km/h)$ , trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc $900(km/h)$ và $920(km/h)$ lần lượt biểu diễn bởi hai vectơ $\overrightarrow{F_{1}}$ và $\overrightarrow{F_{2}}$ với $\overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight)$ . Tính giá trị của $k$ (Làm tròn kết quả đến chữ số thập phân thứ hai).
Chỗ nhập nội dung câu trả lời tự luận
Câu 4: Thông hiểu
Chọn đẳng thức đúng

Cho hình lăng trụ tam giác $ABC.A_{1}B_{1}C_{1}$ . Đặt $\overrightarrow{AA_{1}} = \overrightarrow{a},\overrightarrow{AB} = \overrightarrow{b},\overrightarrow{AC} = \overrightarrow{c},\overrightarrow{BC} = \overrightarrow{d},$ trong các đẳng thức sau, đẳng thức nào đúng?
- A.
  $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} + \overrightarrow{d} = \overrightarrow{0}$ .
- B.
  $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{d}$ .
- C.
  $\overrightarrow{b} - \overrightarrow{c} + \overrightarrow{d} = \overrightarrow{0}$ .
- D.
  $\overrightarrow{a} = \overrightarrow{b} + \overrightarrow{c}$ .
Hình vẽ minh họa

+ Dễ thấy: $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \overrightarrow{0} \Rightarrow \overrightarrow{b} + \overrightarrow{d} - \overrightarrow{c} = \overrightarrow{0}$ .
Câu 5: Thông hiểu
Chọn đáp án thích hợp

Trong không gian cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ . Khi đó $\overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC} + \overrightarrow{SD}$ bằng.
- A.
  $4\overrightarrow{OS}$ .
- B.
  $4\overrightarrow{SO}$ .
- C.
  $2\overrightarrow{SO}$ .
- D.
  $3\overrightarrow{SO}$ .
Do $O$ là tâm của hình bình hành $ABCD$ nên $\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = \overrightarrow{0}$ .

Áp dụng quy tắc ba điểm, ta có

$\overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC} + \overrightarrow{SD}$

$= \left( \overrightarrow{SO} + \overrightarrow{OA} ight) + \left( \overrightarrow{SO} + \overrightarrow{OB} ight) + \left( \overrightarrow{SO} + \overrightarrow{OC} ight) + \left( \overrightarrow{SO} + \overrightarrow{OD} ight)$

$= 4\overrightarrow{SO}$
Câu 6: Thông hiểu
Chọn phương án thíchhợp

Trong không gian $Oxyz$ , cho hai điểm $A(2 ; - 2 ; 1)$ , $B(0; 1 ;2)$ . Tọa độ điểm $M$ thuộc mặt phẳng $(Oxy)$ sao cho ba điểm $A$ , $B$ , $M$ thẳng hàng là
- A.
  $M(4\ ;\ - 5\ ;\ 0)$ .
- B.
  $M(2 ; - 3 ;0)$ .
- C.
  $M(0 ; 0 ;1)$ .
- D.
  $M(4 ; 5; 0)$ .
Ta có: $M \in (Oxy) \Rightarrow M(x\ ;\ y\ ;\ 0)$ ; $\overrightarrow{AB} = ( - 2\ ;\ 3\ ;\ 1);\overrightarrow{AM} = (x - 2\ ;\ y + 2\ ;\ - 1)$ .

Để $A$ , $B$ , $M$ thẳng hàng thì $\overrightarrow{AB}$ và $\overrightarrow{AM}$ cùng phương , khi đó :

$\frac{x - 2}{- 2} = \frac{y + 2}{3} = \frac{- 1}{1} \Leftrightarrow \left\{ \begin{matrix} x = 4 \\ y = - 5 \\ \end{matrix} ight.$ .

Vậy $M(4\ ;\ - 5\ ;\ 0)$ .
Câu 7: Vận dụng
Chọn đáp án đúng

Trong không gian $Oxyz$ cho hình hộp chữ nhật $OABC.EFGH$ có các cạnh $OA = 5$ , $OC = 8$ , $OE = 7$ (xem hình vẽ dưới đây). Tọa độ $H(x;y;z)$ . Tính giá trị biểu thức $P = 50x + 75y + 1000z$
- A.
  7600
- B.
  6580
- C.
  7134
- D.
  6783
Ta có $H \in (yOz)$ và hình chiếu của $H$ lên $Oy$ trùng với $C$ nên $H(0;\ 8;\ 7)$ .

$P = 50x + 75y + 1000z = 50.0 + 75.8 + 1000.7 = 7600$ .
Câu 8: Thông hiểu
Tính thể tích tứ diện

Trong không gian với hệ trục tọa độ $Oxyz$ , cho tọa độ ba điểm $A(1;0;0),B(0;2;0),C(0;0;3)$ . Thể tích tứ diện $OABC$ bằng:
- A.
  $V = \frac{1}{3}$
- B.
  $V = \frac{1}{6}$
- C.
  $V = 1$
- D.
  $V = 2$
Ta có: $\left\{ \begin{matrix} \overrightarrow{OA} = (1;0;0) \Rightarrow OA = 1 \\ \overrightarrow{OB} = (0;2;0) \Rightarrow OB = 2 \\ \overrightarrow{OC} = (0;0;3) \Rightarrow OC = 3 \\ \end{matrix} ight.$ . Dễ thấy tứ diện $OABC$ vuông tại $O$ nên

$V_{OABC} = \frac{1}{6}.OA.OB.OC = \frac{1}{6}.1.2.3 = 1$

Vậy đáp án đúng là: $V = 1$ .
Câu 9: Vận dụng
Tính giá trị của biểu thức

Trong không gian $Oxyz$ , cho $A(1;0;0),\ \ B(0;2;0);M(x - 1;2y - 2;7)$ . Gọi $M'$ là hình chiếu của $M$ trên mặt phẳng $(Oxy)$ . Khi tứ giác $OBM'A$ là hình bình hành thì giá trị $x + y$ bằng?
- A.
  $4$ .
- B.
  $2$ .
- C.
  $1$ .
- D.
  $- 1$ .
$M'$ là hình chiếu của $M$ trên mặt phẳng $(Oxy) \Rightarrow M'(x - 1;2y - 2;0)$ .

$OBM'A$ là hình bình hành

$\Leftrightarrow \overrightarrow{OB} = \overrightarrow{AM'} \Leftrightarrow \left\{ \begin{matrix} 0 = x - 2 \\ 2 = 2y - 2 \\ 0 = 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 2 \\ y = 2 \\ \end{matrix} \right.$ .

Vậy $x + y = 4$ .
Câu 10: Vận dụng
Chọn kết quả đúng nhất

Cho tam giác $ABC$ , thì công thức tính diện tích nào sau đây là đúng nhất.
- A.
  $S = \frac{1}{2}\sqrt{AB^{2}AC^{2} - BC^{2}}$
- B.
  $S = \frac{1}{2}\sqrt{AB^{2}AC^{2} + \frac{1}{2}\left( \overrightarrow{AB}.\overrightarrow{AC} \right)^{2}}$
- C.
  $S = \frac{1}{2}\sqrt{AB^{2}AC^{2} - \frac{1}{2}\left( \overrightarrow{AB}.\overrightarrow{AC} \right)^{2}}$
- D.
  $S = \frac{1}{2}\sqrt{AB^{2}AC^{2} - \left( \overrightarrow{AB}.\overrightarrow{AC} \right)^{2}}$
Ta có:

$S_{ABC} = \frac{1}{2}ABAC\sin A = \frac{1}{2}\sqrt{AB^{2}AB^{2}sin^{2}A}$

$= \frac{1}{2}\sqrt{AB^{2}AC^{2}\left( 1 - cos^{2}A \right)}$

$= \frac{1}{2}\sqrt{AB^{2}AC^{2} - \left( \overrightarrow{AB}.\overrightarrow{AC} \right)^{2}}$ .
Câu 11: Vận dụng

Ghi đáp án đúng vào ô trống

Trong một căn phòng dạng hình hộp chữ nhật với chiều dài 10 m có 1 cây quạt hộp Q đặt ở sàn nhà và 3 ổ cắm điện $A,B,C$ trên tường. Chọn hệ trục tọa độ như hình vẽ sau (đơn vị: mét). Biết cây quạt cách tường $(Oxz)$ 3 m và cách tường $(Oyz)$ 6 m; các ổ cắm điện cách mặt sàn 40 cm, ổ cắm A và B cách bức tường chứa ổ cắm C lần lượt 7 m và 1 m, ổ cắm C cách bức tường chứa 2 ổ cắm còn lại 1,5 m.

Dây điện của quạt hộp Q cần dài tối thiểu bao nhiêu để có thể cắm tới cả 3 ổ $A,\ B,\ C$ (Đáp án làm tròn đến hàng phần trăm)

Đáp án: 6,20||6,2

Đáp án là:

Trong một căn phòng dạng hình hộp chữ nhật với chiều dài 10 m có 1 cây quạt hộp Q đặt ở sàn nhà và 3 ổ cắm điện $A,B,C$ trên tường. Chọn hệ trục tọa độ như hình vẽ sau (đơn vị: mét). Biết cây quạt cách tường $(Oxz)$ 3 m và cách tường $(Oyz)$ 6 m; các ổ cắm điện cách mặt sàn 40 cm, ổ cắm A và B cách bức tường chứa ổ cắm C lần lượt 7 m và 1 m, ổ cắm C cách bức tường chứa 2 ổ cắm còn lại 1,5 m.

Dây điện của quạt hộp Q cần dài tối thiểu bao nhiêu để có thể cắm tới cả 3 ổ $A,\ B,\ C$ (Đáp án làm tròn đến hàng phần trăm)

Đáp án: 6,20||6,2

Tọa độ cây quạt Q là $Q(6;3;0)$

Tọa độ các ổ cắm điện A, B, C lần lượt là: $A\left( 7;0;\frac{2}{5} ight),\ \ B\left( 1;0;\frac{2}{5} ight),\ \ C\left( 0;\frac{3}{2};\frac{2}{5} ight)$

$AQ = 3,19,\ BQ \approx 5,84,\ CQ \approx 6,20$ .
Câu 12: Nhận biết
Định tọa độ hình chiếu

Trong không gian tọa độ $Oxyz$ , hình chiếu vuông góc của điểm $B( - 2;3;1)$ trên trục $Ox$ có tọa độ là:
- A.
  $(2;0;0)$ .
- B.
  $(0; - 3; - 1)$ .
- C.
  $( - 2;0;0)$ .
- D.
  $(0;3;1)$ .
Hình chiếu vuông góc của điểm $B( - 2;3;1)$ trên trục $Ox$ là điểm có tọa độ $( - 2;0;0)$ .
Câu 13: Thông hiểu
Tìm tọa độ điểm B’

Trong không gian hệ trục tọa độ $Oxyz$ , cho hình hộp $ABCCD.A'B'C'D'$ . Biết $A(2;4;0),B(4;0;0),C( - 1;4;7),D'(6;8;10)$ . Tọa độ điểm $B'$ là:
- A.
  $B'(8;4;10)$
- B.
  $B'(6;12;0)$
- C.
  $B'(10;8;6)$
- D.
  $B'(13;0;17)$
Hình vẽ minh họa

Ta có: $\overrightarrow{AD} = \overrightarrow{BC} = ( - 5;4;7) \Rightarrow D( - 3;8; - 7)$

$\overrightarrow{BD} = \overrightarrow{B'D'} = ( - 7;8; - 7) \Rightarrow B'(13;0;17)$
Câu 14: Vận dụng cao
Tính giá trị lớn nhất của biểu thức

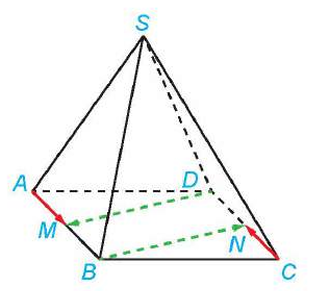
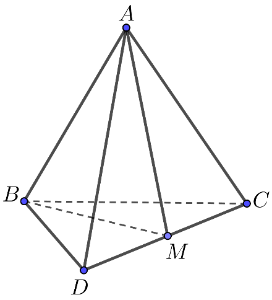
Cho tứ diện $ABCD$ có $BC = DA = a,CA = DB = b,AB = DC = c$ . Gọi $S$ là diện tích toàn phần (tổng diện tích tất cả các mặt). Tính giá trị lớn nhất của $\frac{1}{a^{2}b^{2}} + \frac{1}{b^{2}c^{2}} + \frac{1}{c^{2}a^{2}}$ .
- A.
  $\frac{9}{S^{2}}$
- B.
  $\frac{3}{S}$
- C.
  $\frac{2}{S^{2}}$
- D.
  $\frac{\sqrt{2}}{S}$
Do tứ diện $ABCD$ có $BC = DA = a,CA = DB = b,AB = DC = c$ nên $\Delta BCD = \Delta ADC = \Delta DAB = \Delta CBA$ .

Gọi $S'$ là diện tích và $R$ là bán kính đường tròn ngoại tiếp mỗi mặt đó thì $S = 4S' = \frac{abc}{R}$ , nên bất đẳng thức cần chứng minh:

$\frac{1}{a^{2}b^{2}} + \frac{1}{b^{2}c^{2}} + \frac{1}{c^{2}a^{2}} \leq \frac{9}{S^{2}} \Leftrightarrow a^{2} + b^{2} + c^{2} \leq 9R^{2}$ .

Theo công thức Leibbnitz:

Với điểm $M$ bất kì và $G$ là trọng tâm của tam giác $ABC$ thì

$MA^{2} + MB^{2} + MC^{2}$

$= GA^{2} + GB^{2} +BC^{2} + 3MG^{2}$

$= \frac{1}{3}\left( a^{2} + b^{2} + c^{2} + 9MG^{2}\right)$

Cho $M$ trùng với tâm đường tròn ngoại tiếp tam giác $ABC$ ta được:

$9R^{2} = aa^{2} + b^{2} + c^{2} + 9OG^{2} \geq a^{2} + b^{2} + c^{2}$ .
Câu 15: Nhận biết
Chọn đáp án đúng

Trong không gian $Oxyz$ , mặt phẳng $(\alpha):x - y + 2z - 3 = 0$ đi qua điểm nào sau đây?
- A.
  $\left( 1;1;\frac{3}{2} ight)$
- B.
  $\left( 1; - 1; - \frac{3}{2} ight)$
- C.
  $(1;6;1)$
- D.
  $(0;3;0)$
Xét điểm $\left( 1;1;\frac{3}{2} ight)$ ta có: $1 - 1 + 2.\frac{3}{2} - 3 = 0$ đúng nên $\left( 1;1;\frac{3}{2} ight) \in (\alpha)$ .
Câu 16: Vận dụng
Chọn khẳng định đúng

Trong không gian hệ trục tọa độ $Oxyz$ , cho hình hộp $ABCD.A'B'C'D'$ có tọa độ các điểm $A(1;0;1),B(2;1;2),D(1; - 1;1),C'(4;5; - 5)$ . Tìm tọa độ điểm $A'$ ?
- A.
  $A'(4;6; - 5)$
- B.
  $A'(2;0;2)$
- C.
  $A'(3;5; - 6)$
- D.
  $A'(3;4; - 6)$
Theo quy tắc hình hộp ta có:

$\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA'} = \overrightarrow{AC'}$

$\Rightarrow \overrightarrow{AA'} = \overrightarrow{AB} - \overrightarrow{AD} - \overrightarrow{AC'}$

Lại có $\left\{ \begin{matrix} \overrightarrow{AB} = (1;1;1) = \overrightarrow{i} + \overrightarrow{j} + \overrightarrow{k} \\ \overrightarrow{AD} = (0; - 1;0) = 0.\overrightarrow{i} - \overrightarrow{j} + 0.\overrightarrow{k} \\ \overrightarrow{AC'} = (3;5; - 6) = 3.\overrightarrow{i} + 5\overrightarrow{j} - 6\overrightarrow{k} \\ \end{matrix} ight.$ do đó $\Rightarrow \overrightarrow{AA'} = 2\overrightarrow{i} + 5\overrightarrow{j} - 6\overrightarrow{k}$ hay $\overrightarrow{AA'} = (3;5; - 6)$

Suy ra $A'(3;5; - 6)$
Câu 17: Thông hiểu
Chọn đáp án đúng

Trong không gian hệ trục tọa độ $Oxyz$ , cho các điểm $A(1;2; - 1),B(2; - 1;3),C( - 3;5;1)$ . Tìm tọa độ điểm $D$ sao cho tứ giác $ABCD$ là hình bình hành?
- A.
  $D( - 2;8; - 3)$
- B.
  $D( - 4;8; - 5)$
- C.
  $D( - 2;2;5)$
- D.
  $D( - 4;8; - 3)$
Giả sử điểm $D(x;y;z)$ ta có $ABCD$ là hình bình hành nên $\overrightarrow{AB} = \overrightarrow{DC}$

$\Leftrightarrow \left\{ \begin{matrix} 2 - 1 = - 3 - x \\ - 1 - 2 = 5 - y \\ 3 - ( - 1) = 1 - z \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = - 4 \\ y = 8 \\ z = - 3 \\ \end{matrix} ight.$ . Vậy tọa độ điểm $D( - 4;8; - 3)$ .
Câu 18: Nhận biết
Tìm các vectơ đồng phẳng

Trong không gian cho hình hộp $ABCD.A'B'C'D'$ . Hỏi bốn vectơ nào có giá cùng thuộc một mặt phẳng?
- A.
  $\overrightarrow{AC};\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AC'}$
- B.
  $\overrightarrow{A'D};\overrightarrow{AA'};\overrightarrow{A'D'};\overrightarrow{DD'}$
- C.
  $\overrightarrow{AC};\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AA'}$
- D.
  $\overrightarrow{AB'};\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AA'}$
Hình vẽ minh họa

Từ hình vẽ ta thấy các vectơ $\overrightarrow{A'D};\overrightarrow{AA'};\overrightarrow{A'D'};\overrightarrow{DD'}$ có giá cùng thuộc một mặt phẳng $(AA'D'D)$ .
Câu 19: Thông hiểu
Định tọa độ trọng tâm tam giác ABC

Trong không gian $(Oxyz)$ cho $\overrightarrow{OA} = \overrightarrow{i} - 2\overrightarrow{j} + 3\overrightarrow{k},$ điểm $B(3; - 4;1)$ và điểm $C(2;0; - 1).$ Tọa độ trọng tâm của tam giác ABC là
- A.
  $(1; - 2;3).$
- B.
  $( - 2;2; - 1).$
- C.
  $(2; - 2;1).$
- D.
  $( - 1;2; - 3).$
Ta có $\overrightarrow{OA} = \overrightarrow{i} - 2\overrightarrow{j} + 3\overrightarrow{k} = > A(1; - 2;3).$

Gọi G là trọng tâm của tam giác ABC ta có

$\left\{ \begin{matrix} x_{G} = \dfrac{x_{A} + x_{B} + x_{C}}{3} = \dfrac{1 + 3 + 2}{3} = 2 \\ y_{G} = \dfrac{y_{A} + y_{B} + y_{C}}{3} = \dfrac{- 2 - 4 + 0}{3} = - 2 \\ z_{G} = \dfrac{z_{A} + z_{B} + z_{C}}{3} = \dfrac{3 + 1 - 1}{3} = 1 \\ \end{matrix} ight.$ .

Vậy $G(2; - 2;1).$
Câu 20: Thông hiểu
Tìm tọa độ điểm C

Trong không gian $Oxyz$ , cho hai điểm $A( - 2\ ;\ 4\ ;\ 1)$ và $B(4\ ;\ 5\ ;\ 2)$ . Điểm $C$ thỏa mãn $\overrightarrow{OC} = \overrightarrow{BA}$ có tọa độ là
- A.
  $( - 6\ ;\ \ - 1\ ;\ - 1)$ .
- B.
  $( - 2\ ;\ \ - 9\ ;\ - 3)$ .
- C.
  $(6\ ;\ \ 1\ ;\ 1)$ .
- D.
  $(2\ ;\ \ 9\ ;\ 3)$ .
Gọi $C(x\ ;\ y\ ;\ z)$ .

Ta có $\overrightarrow{OC} = (x\ ;\ y\ ;\ z)$ , $\overrightarrow{BA} = ( - 6\ ;\ - 1\ ;\ - 1)$ .

Khi đó $\overrightarrow{OC} = \overrightarrow{BA} \Leftrightarrow \left\{ \begin{matrix} x = - 6 \\ y = - 1 \\ x = - 1 \\ \end{matrix} ight.$ .

Vậy $C( - 6\ ;\ - \ 1\ ; - \ 1)$ .
Câu 21: Vận dụng
Tính giá trị biểu thức

Trong không gian $Oxyz$ cho hai điểm $A(1\ ;\ \ 5\ ;\ 0)$ , $B(3\ ;\ 3\ ;\ 6)$ và đường thẳng $d:\ \frac{x + 1}{2} = \frac{y - 1}{- 1} = \frac{z}{2}$ . Điểm $M(a\ ;\ b\ ;\ c)$ thuộc đường thẳng $d$ sao cho chu vi tam giác $MAB$ nhỏ nhất. Khi đó biểu thức $a + 2b + 3c$ bằng
- A.
  $5$ .
- B.
  $7$ .
- C.
  $9$ .
- D.
  $3$ .
Ta có $AB = \sqrt{44}$ không đổi.

Do đó chu vi tam giác $MAB$ nhỏ nhất khi $(MA + MB)$ đạt giá trị nhỏ nhất.

$M \in (d) \Rightarrow M( - 1 + 2t\ ;\ 1 - t\ ;\ 2t)$ .

$MA = \sqrt{9t^{2} + 20} = \sqrt{(3t)^{2} + \left( 2\sqrt{5} ight)^{2}}$ , $MB = \sqrt{9t^{2} - 36t + 56} = \sqrt{(6 - 3t)^{2} + \left( 2\sqrt{5} ight)^{2}}$ .

Chọn $\overrightarrow{u} = \left( 3t\ ;\ 2\sqrt{5}\ ;\ 0 ight) \Rightarrow \left| \overrightarrow{u} ight| = \sqrt{(3t)^{2} + \left( 2\sqrt{5} ight)^{2}}$ .

Chọn $\overrightarrow{v} = \left( 6 - 3t\ ;\ 2\sqrt{5}\ ;\ 0 ight) \Rightarrow \left| \overrightarrow{v} ight| = \sqrt{(6 - 3t)^{2} + \left( 2\sqrt{5} ight)^{2}}$

$\Rightarrow \overrightarrow{u} + \overrightarrow{v} = \left( 6\ ;\ 4\sqrt{5}\ ;\ 0 ight) \Rightarrow \left| \overrightarrow{u} + \overrightarrow{v} ight| = 2\sqrt{29}$ .

Theo tính chất vecto $\left| \overrightarrow{u} ight| + \left| \overrightarrow{v} ight| \geq \left| \overrightarrow{u} + \overrightarrow{v} ight| = 2\sqrt{29}$ .

Dấu $" = "$ xảy ra khi và chỉ khi $\overrightarrow{u}$ cùng hướng với $\overrightarrow{v}$ $\Leftrightarrow t = 1$ .

Suy ra $MA + MB = \left| \overrightarrow{u} ight| + \left| \overrightarrow{v} ight| \geq 2\sqrt{29}$ .

Do đó $MA + MB$ đạt giá trị nhỏ nhất bằng $2\sqrt{29}$ khi $t = 1$ $\Rightarrow$ $M(1\ ;\ 0\ ;\ 2)$ .

Vậy $a + 2b + 3c = 1 + 2.0 + 3.2 = 7$ .
Câu 22: Nhận biết
Chọn khẳng định sai

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{a} = (1; - 2;0)$ và $\overrightarrow{b} = ( - 2;3;1)$ . Khẳng định nào sau đây sai?
- A.
  $\overrightarrow{a}.\overrightarrow{b} = - 8$
- B.
  $2\overrightarrow{a} = (2; - 4;0)$
- C.
  $\overrightarrow{a} + \overrightarrow{b} = ( - 1;1; - 1)$
- D.
  $\left| \overrightarrow{b} ight| = \sqrt{11}$
Ta có: $\overrightarrow{a} + \overrightarrow{b} = ( - 1;1;1)$ suy ra “ $\overrightarrow{a} + \overrightarrow{b} = ( - 1;1; - 1)$ ” là khẳng định sai.
Câu 23: Nhận biết
Tìm tọa độ điểm M

Trong không gian $Oxyz$ , cho điểm $M$ thỏa mãn $\overrightarrow{MO} = 3\overrightarrow{k} - 2\overrightarrow{i} + 4\overrightarrow{j}$ . Tọa độ điểm $M$ bằng
- A.
  $(3; - 2;4)$ .
- B.
  $( - 2;4;3)$ .
- C.
  $(2; - 4; - 3)$ .
- D.
  $(3;2;4)$ .
Ta có: $\overrightarrow{MO} =3 \overrightarrow{k} - 2\overrightarrow{i} + 4\overrightarrow{j}$ $\Rightarrow M(2; - 4; - 3)$
Câu 24: Thông hiểu
Tìm tọa độ biểu thức vectơ

Cho $\overrightarrow{AB} = (5; - 3;2),\overrightarrow{AC} = (4;2;1)$ . Tọa độ của $\overrightarrow{a} = 2\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}$ là:
- A.
  $\left( 10; - 5;\frac{9}{2} ight)$ .
- B.
  $(12; - 5;9)$ .
- C.
  $\left( 12; - 5;\frac{9}{2} ight)$ .
- D.
  $\left( 12; - 2;\frac{9}{2} ight)$ .
Ta có:

$\overrightarrow{a} = 2\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}$

$= \left( 2.5 + \frac{1}{2}.4;2.( - 3) + \frac{1}{2}.2;2.2 + \frac{1}{2}.1 ight)$

$= \left( 12; - 5;\frac{9}{2} ight)$
Câu 25: Thông hiểu
Tìm tọa độ điểm D thỏa mãn yêu cầu

Trong không gian hệ trục tọa độ $Oxyz$ , cho các điểm $A(0; - 1;1),B( - 2;1; - 1),C( - 1;3;2)$ . Biết rằng tứ giác $ABCD$ là hình bình hành, khi đó tọa độ điểm $D$ là:
- A.
  $D\left( - 1;1;\frac{2}{3} ight)$
- B.
  $D(1;3;4)$
- C.
  $D(1;1;4)$
- D.
  $D( - 1; - 3; - 2)$
Giả sử điểm $D(x;y;z)$ ta có $ABCD$ là hình bình hành nên $\overrightarrow{BA} = \overrightarrow{CD}$

$\Leftrightarrow \left\{ \begin{matrix} x + 1 = 2 \\ y - 3 = - 2 \\ z - 2 = 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 1 \\ y = 1 \\ z = 4 \\ \end{matrix} ight.$ . Vậy tọa độ điểm $D(1;1;4)$
Câu 26: Nhận biết
Chọn khẳng định đúng

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{u} = (1;2;3)$ và $\overrightarrow{v} = ( - 5;1;1)$ . Khẳng định nào sau đây đúng?
- A.
  $\overrightarrow{u} =\overrightarrow{v}$
- B.
  $\overrightarrow{u}\bot\overrightarrow{v}$
- C.
  $\left| \overrightarrow{u} ight| =\left| \overrightarrow{v} ight|$
- D.
  $\overrightarrow{u}//\overrightarrow{v}$
Ta có: $\overrightarrow{u}.\overrightarrow{v} = 1.( - 5) +2.1 + 3.1 = 0 \Rightarrow\overrightarrow{u}\bot\overrightarrow{v}$
Vậy khẳng định đúng là $\overrightarrow{u}\bot\overrightarrow{v}$
Câu 27: Thông hiểu

Ghi đáp án vào ô trống

Sự chuyển động của máy bay A được thể hiện trong không gian $Oxyz$ như sau: Máy bay khởi hành từ $B(0;0;2)$ chuyển động thẳng đều (Tính theo phút) với vận tốc được biểu thị theo véc tơ $\overrightarrow{v}(1;4;5)$ . Sau khi khởi hành được 30 phút, máy bay ở vị trí $M(x;y;z)$ . Tính $P = 3x + y + z$

Đáp án: 362

Đáp án là:

Sự chuyển động của máy bay A được thể hiện trong không gian $Oxyz$ như sau: Máy bay khởi hành từ $B(0;0;2)$ chuyển động thẳng đều (Tính theo phút) với vận tốc được biểu thị theo véc tơ $\overrightarrow{v}(1;4;5)$ . Sau khi khởi hành được 30 phút, máy bay ở vị trí $M(x;y;z)$ . Tính $P = 3x + y + z$

Đáp án: 362

Ta có:

Quãng đường máy bay di chuyển là:

$BM = \left| \overrightarrow{v} ight|.t \Rightarrow \overrightarrow{BM} = \overrightarrow{v}.30 = (30;120;150)$

$\Rightarrow \left\{ \begin{matrix} x = 30 \\ y = 120 \\ z - 2 = 150 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} x = 30 \\ y = 120 \\ z = 152 \\ \end{matrix} ight.\ ight.$

Khi đó: $P = 3.30 + 120 + 152 = 362$
Câu 28: Thông hiểu
Chọn khẳng định đúng

Cho tứ diện $ABCD$ . Gọi $P,\ Q$ là trung điểm của $AB$ và $CD$ . Chọn khẳng định đúng?
- A.
  $\overrightarrow{PQ} = \frac{1}{4}\left( \overrightarrow{BC} + \overrightarrow{AD} ight)$ .
- B.
  $\overrightarrow{PQ} = \frac{1}{2}\left( \overrightarrow{BC} + \overrightarrow{AD} ight)$ .
- C.
  $\overrightarrow{PQ} = \frac{1}{2}\left( \overrightarrow{BC} - \overrightarrow{AD} ight)$ .
- D.
  $\overrightarrow{PQ} = \overrightarrow{BC} + \overrightarrow{AD}$ .
Ta có : $\overrightarrow{PQ} = \overrightarrow{PB} + \overrightarrow{BC} + \overrightarrow{CQ}$ và $\overrightarrow{PQ} = \overrightarrow{PA} + \overrightarrow{AD} + \overrightarrow{DQ}$

nên $2\overrightarrow{PQ} = \left( \overrightarrow{PA} + \overrightarrow{PB} ight) + \overrightarrow{BC} + \overrightarrow{AD} + \left( \overrightarrow{CQ} + \overrightarrow{DQ} ight) = \overrightarrow{BC} + \overrightarrow{AD}$ .

Vậy $\overrightarrow{PQ} = \frac{1}{2}\left( \overrightarrow{BC} + \overrightarrow{AD} ight)$
Câu 29: Vận dụng
Chọn đáp án đúng

Trong không gian $Oxyz$ , cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $A'\left( \sqrt{3}\ ;\ - 1\ ;\ 1 \right)$ , hai đỉnh $B\ ,\ C$ thuộc trục $Oz$ và $AA' = 1$ ( $C$ không trùng với $O$ ). Biết véctơ $\overrightarrow{u} = (a\ ;\ b\ ;\ 2)$ với $a\ ,\ b\mathbb{\in R}$ là một véctơ chỉ phương của đường thẳng $A'C$ . Tính $T = a^{2} + b^{2}$ .
- A.
  $T = 5$ .
- B.
  $T = 16$ .
- C.
  $T = 4$ .
- D.
  $T = 9$ .
Hình vẽ minh họa

Gọi $M$ là trung điểm $BC$ .

Khi đó có $\left\{ \begin{matrix} AM\bot BC \\ AA'\bot BC \\ \end{matrix} ight.\ \Rightarrow BC\bot A'M$ tại $M \Rightarrow M$ là hình chiếu của $A'$ trên trục $Oz$

$A'\left( \sqrt{3}\ ;\ - 1\ ;\ 1 ight) \Rightarrow M(0\ ;\ 0\ ;\ 1)$ và $A'M = 2$ .

Ta có: $AM = \sqrt{A'M^{2} - A{A'}^{2}} = \sqrt{3}$ .

Mà tam giác $ABC$ đều nên $AM = \frac{\sqrt{3}}{2}BC = \sqrt{3} \Rightarrow BC = 2 \Rightarrow MC = 1$ .

Vì $C$ thuộc trục $Oz$ và $C$ không trùng với $O$ nên gọi $C(0\ ;\ 0\ ;\ c)$ , $c eq 0$ .

$\overrightarrow{MC} = (0\ ;\ 0\ ;\ c - 1)$ $\Rightarrow MC = |c - 1|$ ; $MC = 1$ $\Leftrightarrow |c - 1| = 1$ $\Leftrightarrow \left\lbrack \begin{matrix} c = 0\ (L) \\ c = 2 \\ \end{matrix} ight.$ $\Rightarrow C(0\ ;\ 0\ ;\ 2)$ .

$\overrightarrow{A'C} = \left( -\sqrt{3} ; 1 ;1 ight)$ là một véctơ chỉ phương của đường thẳng $A'C$

$\Rightarrow$ $\overrightarrow{u} = \left( - 2\sqrt{3}\ ;\ 2\ ;\ 2 ight)$ cũng là một véctơ chỉ phương của đường thẳng $A'C$ .

Vậy $a = - 2\sqrt{3};\ \ b = 2 \Rightarrow T = a^{2} + b^{2} = 16.$
Câu 30: Vận dụng cao
Tìm tọa độ điểm M thỏa mãn điều kiện

Trong không gian $Oxyz$ , cho $\overrightarrow{OA} = \overrightarrow{i} + \overrightarrow{j} - 3\overrightarrow{k}$ , $B(2;2;1)$ . Tìm tọa độ điểm $M$ thuộc trục tung sao cho $MA^{2} + MB^{2}$ nhỏ nhất.
- A.
  $M(0\ ; - 2\ ;0)$ .
- B.
  $M\left( 0\ ;\frac{3}{2}\ ;0 ight)$ .
- C.
  $M(0 ; - 3 ;0)$ .
- D.
  $M(0\ ; - 4\ ;0)$ .
Khi đó:

$MA^{2} + MB^{2} = {\overrightarrow{MA}}^{2} + {\overrightarrow{MB}}^{2}$

$= \left( \overrightarrow{MI} + \overrightarrow{IA} ight)^{2} + \left( \overrightarrow{MI} + \overrightarrow{IB} ight)^{2}$

$= 2{\overrightarrow{MI}}^{2} + {\overrightarrow{IA}}^{2} + {\overrightarrow{IB}}^{2} + 2\overrightarrow{MI}.\left( \overrightarrow{IA} + \overrightarrow{IB} ight)$

$= 2MI^{2} + IA^{2} + IB^{2} = 2MI^{2} + 9$ .

Do đó $MA^{2} + MB^{2}$ đạt giá trị nhỏ nhất khi và chỉ khi $MI$ có độ dài ngắn nhất, điều này xảy ra khi và chỉ khi $M$ là hình chiếu vuông góc của $I$ trên trục tung.

Phương trình mặt phẳng $(P)$ đi qua $I$ và vuông góc với trục tung là

$0.\left( x - \frac{3}{2} ight) + 1.\left( y - \frac{3}{2} ight) + 0.(z + 1) = 0$ hay $(P):y - \frac{3}{2} = 0$ .

Phương trình tham số của trục tung là $\left\{ \begin{matrix} x = 0 \\ y = t \\ z = 0 \\ \end{matrix} ight.$ .

Tọa độ điểm $M$ cần tìm là nghiệm $(x\ ;y\ ;z)$ của hệ phương trình:

$\left\{ \begin{matrix} x = 0 \\ y = t \\ z = 0 \\ y - \frac{3}{2} = 0 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} x = 0 \\ y = \frac{3}{2} \\ z = 0 \\ \end{matrix} ight.$ .

Vậy $M\left( 0\ ;\frac{3}{2}\ ;0 ight)$ .
Câu 31: Nhận biết
Chọn mệnh đề sai

Mệnh đề nào sau đây sai?
- A.
  Vectơ không là vectơ có điểm đầu và điểm cuối trùng nhau.
- B.
  Hai vectơ có độ dài bằng nhau và cùng phương thì hai vectơ đó bằng nhau.
- C.
  Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
- D.
  Độ dài vectơ là độ dài đoạn thẳng có hai đầu mút là điểm đầu và điểm cuối của vectơ đó.
Hai vectơ có độ dài bằng nhau và cùng hướng thì hai vectơ đó bằng nhau.
Câu 32: Thông hiểu
Tính giá trị biểu thức

Trong không gian với hệ trục tọa độ $Oxyz$ , cho hai điểm $B(1;2; - 3),C(7;4 - 2)$ . Tìm tọa độ điểm $E$ thỏa mãn đẳng thức $\overrightarrow{CE} = 2\overrightarrow{EB}$ ?
- A.
  $E\left( 3;\frac{8}{3}; - \frac{8}{3} ight)$
- B.
  $E\left( \frac{8}{3};3; - \frac{8}{3} ight)$
- C.
  $E\left( 3;3; - \frac{8}{3} ight)$
- D.
  $E\left( 1;2;\frac{1}{3} ight)$
Gọi $E(x;y;z)$

Ta có: $\left\{ \begin{matrix} \overrightarrow{CE} = (x - 7;y - 4;z + 2) \\ 2\overrightarrow{EB} = (2 - 2x;4 - 2y; - 6 - 2z) \\ \end{matrix} ight.$

Theo bài ra ta có:

$\overrightarrow{CE} =2\overrightarrow{EB} \Leftrightarrow \left\{ \begin{matrix}x - 7 = 2 - 2x \\y - 4 = 4 - 2y \\z + 2 = - 6 - 2z \\\end{matrix} ight.$ $\Leftrightarrow \left\{ \begin{matrix}x = 3 \\y = \dfrac{8}{3} \\z = - \dfrac{8}{3} \\\end{matrix} ight.\ \Rightarrow E\left( 3;\frac{8}{3}; - \dfrac{8}{3}ight)$

Vậy điểm E có tọa độ là $E\left( 3;\frac{8}{3}; - \frac{8}{3} ight)$ .
Câu 33: Thông hiểu
Chọn khẳng định đúng

Cho ba vectơ $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$ không đồng phẳng. Xét các vectơ $\overrightarrow{x} = 2\overrightarrow{a} +\overrightarrow{b},$ $\overrightarrow{y} = \overrightarrow{a} -\overrightarrow{b} - \overrightarrow{c},$ $\overrightarrow{z} = -3\overrightarrow{b} - 2\overrightarrow{c}$ . Khẳng định nào dưới đây đúng?
- A.
  Ba vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ đồng phẳng.
- B.
  Hai vectơ $\overrightarrow{x},\overrightarrow{a}$ cùng phương.
- C.
  Hai vectơ $\overrightarrow{x},\overrightarrow{b}$ cùng phương.
- D.
  Ba vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ đôi một cùng phương.
Giả sử ba vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ đồng phẳng, khi đó $\overrightarrow{x} =m\overrightarrow{y} + n\overrightarrow{z}$

Ta có: $\left\{ \begin{matrix}m\overrightarrow{y} = m\overrightarrow{a} - m\overrightarrow{b} -m\overrightarrow{c} \\overrightarrow{z} = - 3n\overrightarrow{b} - 2n\overrightarrow{c} \\\end{matrix} ight.$

$\Rightarrow m\overrightarrow{y} +n\overrightarrow{z} = m\overrightarrow{a} - (m + 3n)\overrightarrow{b} -(m + 2n)\overrightarrow{c}$

Khi đó:

$2\overrightarrow{a} + \overrightarrow{b}= m\overrightarrow{a} - (m + 3n)\overrightarrow{b} - (m +2n)\overrightarrow{c}$

$\Leftrightarrow \left\{ \begin{matrix} m = 2 \\ m + 3n = - 1 \\ m + 2n = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m = 2 \\ n = - 1 \\ \end{matrix} ight.$

Vậy ba vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ đồng phẳng.

Vậy khẳng định đúng là: “Ba vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ đồng phẳng”.
Câu 34: Thông hiểu
Xác định độ lớn góc giữa hai vectơ

Cho hình chóp $S.ABC$ có $SA = SB = SC$ và $\widehat{ASB} = \widehat{BSC} = \widehat{CSA}$ . Góc giữa cặp vectơ $\overrightarrow{SA}$ và $\overrightarrow{BC}$ là:
- A.
  $120^{0}$
- B.
  $90^{0}$
- C.
  $45^{0}$
- D.
  $60^{0}$
Ta có: $\overrightarrow{SA}.\overrightarrow{BC} = \overrightarrow{SA}.\left( \overrightarrow{SC} - \overrightarrow{SB} ight)$

$= \overrightarrow{SA}.\overrightarrow{SC} - \overrightarrow{SA}.\overrightarrow{SB}$

$= \left| \overrightarrow{SA}ight|.\left| \overrightarrow{SC} ight|.\cos\widehat{ASC} - \left|\overrightarrow{SA} ight|.\left| \overrightarrow{SB}ight|.\cos\widehat{ASB} = 0$

Vậy góc giữa cặp vectơ $\overrightarrow{SA}$ và $\overrightarrow{BC}$ là $90^{0}$ .
Câu 35: Nhận biết
Chọn đáp án sai

Tính chất nào sau đây sai?
- A.
  $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$
- B.
  $\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{b} - \overrightarrow{a}$
- C.
  $\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{a} + \left( - \overrightarrow{b} ight)$
- D.
  $\left( \overrightarrow{a} + \overrightarrow{b} ight) + \overrightarrow{c} = \overrightarrow{a} + \left( \overrightarrow{b} + \overrightarrow{c} ight)$
Tính chất sai là: $\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{b} - \overrightarrow{a}$
Câu 36: Thông hiểu
Tính giá trị biểu thức

Cho tam giác $ABC$ . Lấy điểm $S$ nằm ngoài mặt phẳng $(ABC)$ . Trên đoạn $SA$ lấy điểm $M$ sao cho $\overrightarrow{MS} = - 2\overrightarrow{MA}$ và trên đoạn $BC$ lấy điểm $N$ sao cho $\overrightarrow{NB} = - \frac{1}{2}\overrightarrow{NC}$ . Biết biểu diễn $\overrightarrow{MN} = m.\overrightarrow{AB} + n.\overrightarrow{SC}$ là duy nhất. Tính giá trị biểu thức $T = m + n$ ?
- A.
  $T = 0$
- B.
  $T = 1$
- C.
  $T = 2$
- D.
  $T = 3$
Hình vẽ minh họa

Theo giả thiết ta có: $\overrightarrow{MS} = - 2\overrightarrow{MA}$ ; $\overrightarrow{NB} = - \frac{1}{2}\overrightarrow{NC}$

Lấy điểm P trên cạnh AC sao cho $\overrightarrow{PC} = - 2\overrightarrow{PA}$ . Khi đó:

$\overrightarrow{MN} = \overrightarrow{MP} + \overrightarrow{PN} = \frac{1}{3}\overrightarrow{SC} + \frac{2}{3}\overrightarrow{AB}$

$\Rightarrow \left\{ \begin{matrix}m = \dfrac{2}{3} \ = \dfrac{1}{3} \\\end{matrix} ight.\ \Rightarrow T = 1$
Câu 37: Thông hiểu
Tính giá trị biểu thức

Trong không gian $Oxyz$ , cho điểm $M$ thỏa mãn $\overrightarrow{OM} = (2x - 4)\overrightarrow{i} -4\overrightarrow{j} + (y - 1) \overrightarrow{k}$ . Khi điểm $M \in Oy$ thì giá trị $x + 2y$ bằng?
- A.
  $2$ .
- B.
  $4$ .
- C.
  $1$ .
- D.
  $3$ .
Ta có:

$\left\{ \begin{matrix} \overrightarrow{OM} = (2x - 4)\overrightarrow{i} - 4\overrightarrow{j} + (y - 1)\overrightarrow{k} \\ M \in Oy \\ \end{matrix} ight.$

$\Rightarrow \left\{ \begin{matrix} 2x - 4 = 0 \\ y - 1 = 0 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} x = 2 \\ y = 1 \\ \end{matrix} ight.$

Vậy $x + 2y = 4$
Câu 38: Nhận biết
Chọn đáp án thích hợp

Cho hình hộp $ABCD.A'B'C'D'$ . Gọi $M$ và $N$ lần lượt là trung điểm của $BC$ và $CD$ . Vectơ nào sau đây bằng $2\overrightarrow{MN}$ ?
- A.
  $\overrightarrow{AD}$ .
- B.
  $\overline{A'C'}$ .
- C.
  $\overline{B'D'}$ .
- D.
  $\overrightarrow{BC}$ .
Ta có $\overrightarrow{B'D'}$ cùng hướng với $\overrightarrow{MN}$ và $B'D' = 2MN$ , suy ra $\overrightarrow{B'D'} =2\overrightarrow{MN}$
Câu 39: Nhận biết
Tính góc giữa hai vecto

Cho hình lập phương $ABCD.EFGH$ . Hãy xác định góc giữa cặp vectơ $\overrightarrow{AB}$ và $\overrightarrow{EG}$ ?
- A.
  $90{^\circ}$
- B.
  $60{^\circ}$
- C.
  $45{^\circ}$
- D.
  $120{^\circ}$
Hình vẽ minh họa

Ta có: $EG//AC$ (do $ACGE$ là hình chữ nhật)

$\Rightarrow \left( \overrightarrow{AB},\overrightarrow{EG} ight) = \left( \overrightarrow{AB},\overrightarrow{AC} ight) = \widehat{BAC} = 45{^\circ}$
Câu 40: Nhận biết
Tìm số thực m thỏa mãn điều kiện

Trong không gian với hệ trục tọa độ $Oxyz$ , cho $\overrightarrow{u} = (2; - 1;1)$ và $\overrightarrow{v} = (0; - 3; - m)$ . Tìm số thực $m$ sao cho tích vô hướng $\overrightarrow{u}.\overrightarrow{v} = 1$ .
- A.
  $m = 4$ .
- B.
  $m = 2$ .
- C.
  $m = 3$ .
- D.
  $m = - 2$ .
Ta có: $\overrightarrow{u}.\overrightarrow{v} = 1 \Leftrightarrow 3 - m = 1 \Leftrightarrow m = 2$ .

Tải file làm trên giấy

Chia sẻ bởi:
Khang Anh

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Đấu Trường Tri Thức

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề kiểm tra 45 phút Chương 2 Vectơ và hệ trục tọa độ trong không gian

Chúc mừng Bạn đã hoàn thành bài!

Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Chương II. Vectơ và hệ trục tọa độ trong không gian

Chương III. Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm

Chương IV. Nguyên hàm và tích phân

Chương V. Phương pháp tọa độ trong không gian

Chương VI. Xác suất có điều kiện

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Đấu Trường Tri Thức

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề kiểm tra 45 phút Chương 2 Vectơ và hệ trục tọa độ trong không gian

Đổi điểm làm bài

Đổi điểm làm bài

Chúc mừng Bạn đã hoàn thành bài!

Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Chương II. Vectơ và hệ trục tọa độ trong không gian

Chương III. Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm

Chương IV. Nguyên hàm và tích phân

Chương V. Phương pháp tọa độ trong không gian

Chương VI. Xác suất có điều kiện