Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Khóa học Lớp 12 Toán 12 - Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề kiểm tra 45 phút Chương 4 Nguyên hàm và tích phân

Mô tả thêm:

Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 4: Nguyên hàm và tích phân Toán 12 sách Kết nối tri thức các em nhé!
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Vận dụng cao

    Ghi đáp án vào ô trống

    Cho hàm số f(x) là hàm số chẵn, liên tục trên đoạn \lbrack -1;1brack và \int_{-1}^{1}{f(x)dx} = 4. Tính tích phân I = \int_{- 1}^{1}{\frac{f(x)}{1 +e^{x}}dx}?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số f(x) là hàm số chẵn, liên tục trên đoạn \lbrack -1;1brack và \int_{-1}^{1}{f(x)dx} = 4. Tính tích phân I = \int_{- 1}^{1}{\frac{f(x)}{1 +e^{x}}dx}?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 2: Nhận biết

    Chọn khẳng định đúng

    Giả sử hàm số F(x) là một nguyên hàm của hàm số f(x) trên K. Khẳng định nào sau đây đúng.

    Khẳng định đúng là: “Với mỗi nguyên hàm G của f trên K thì tồn tại một hằng số C sao cho G(x) = F(x) + C với x thuộc K.”

  • Câu 3: Nhận biết

    Chọn khẳng định đúng

    Công thức tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y = f(x);y = g(x) liên tục trên đoạn \lbrack a;bbrack và hai đường thẳng x = a;x = b;a < b là

    Ta có hình phẳng giới hạn bởi \left\{ \begin{matrix} \left( C_{1} ight):y = f(x) \\ \left( C_{2} ight):y = g(x) \\ x = a \\ x = b \\ \end{matrix} ight. là S = \int_{a}^{b}{\left| f(x) - g(x) ight|dx}.

  • Câu 4: Thông hiểu

    Tìm giá trị tham số a

    Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị y = x^{2} - ax với trục hoành (a eq 0). Quay hình (H) xung quanh trục hoành ta thu được khối tròn xoay có thể tích V = \frac{16\pi}{15}. Tìm a?

    Phương trình hoành độ giao điểm

    x^{2} - ax = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = a \\ \end{matrix} ight.

    Trường hợp 1: Với a > 0 thì thể tích khối tròn xoay là:

    V = \pi\int_{0}^{a}{\left( x^{2} - ax ight)^{2}dx} = \pi\left. \ \left( \frac{x^{5}}{5} - \frac{ax^{4}}{2} + \frac{a^{2}x^{3}}{3} ight) ight|_{0}^{a} = \frac{a^{5}\pi}{30}

    \Rightarrow \frac{a^{5}\pi}{30} = \frac{16\pi}{15} \Rightarrow a = 2

    Trường hợp 2: Với a < 0 thì thể tích khối tròn xoay là:

    V = \pi\int_{a}^{0}{\left( x^{2} - ax ight)^{2}dx} = \pi\left. \ \left( \frac{x^{5}}{5} - \frac{ax^{4}}{2} + \frac{a^{2}x^{3}}{3} ight) ight|_{a}^{0} = - \frac{a^{5}\pi}{30}

    \Rightarrow - \frac{a^{5}\pi}{30} = \frac{16\pi}{15} \Rightarrow a = - 2

    Vậy a = \pm 2.

  • Câu 5: Thông hiểu

    Tính diện tích hình phẳng

    Tính diện tích hình phẳng S giới hạn bởi đồ thị các hàm số y = 2^{x} và y = 3 - x, trục hoành và trục tung.

    Giao điểm 2^{x} = 3 - x \Rightarrow Nhẩm được nghiệm 1

    S = \int_{0}^{1}\left| 2^{x} + x - 3 ight|dx = \left| \frac{2^{x}}{\ln2} + \frac{x^{2}}{2} - 3x ight|_{0}^{1}

    = \frac{2}{\ln2} + \frac{1}{2} - 3 - \frac{1}{\ln2} = \frac{1}{\ln2} - \frac{5}{2}

  • Câu 6: Vận dụng

    Tìm tập nghiệm S của phương trình

    Cho F(x) là nguyên hàm của hàm số y = f\left( x ight) = \frac{1}{{{e^x} + 3}} thỏa mãn F\left( 0 ight) = - \frac{{ - 1}}{3}\ln 4. Tìm tập nghiệm S của phương trình 3F\left( x ight) + \ln \left( {{e^x} + 3} ight) = 2

    F\left( x ight) = \int {\frac{1}{{{e^x} + 3}}dx} = \int {\frac{{{e^x}}}{{{e^x}\left( {{e^x} + 3} ight)}}dx}

     Đặt t = {e^x} \Rightarrow dt = {e^x}dx

    \int {\frac{{{e^x}}}{{{e^x}\left( {{e^x} + 3} ight)}}dx} = \int {\frac{1}{{t\left( {t + 3} ight)}}dt}

    = \int {\left( {\frac{1}{{3t}} - \frac{1}{{3\left( {t + 3} ight)}}} ight)dt = \frac{{\ln |t|}}{3} - \frac{{\ln |t + 3|}}{3} + C}

    = \frac{{\ln \left( {{e^x}} ight)}}{3} - \frac{{\ln \left( {{e^x} + 3} ight)}}{3} + C = \frac{x}{3} - \frac{{\ln \left( {{e^x} + 3} ight)}}{3} + C

    F\left( 0 ight) = - \frac{1}{3}\ln 4 \Rightarrow - \frac{{\ln 4}}{3} + C = - \frac{1}{3}\ln 4 \Rightarrow C = 0

    Ta có:

    \begin{matrix} 3F\left( x ight) + \ln \left( {{e^x} + 3} ight) = 2 \hfill \\ \Leftrightarrow 3\left[ {\dfrac{x}{3} - \dfrac{{\ln \left( {{e^x} + 3} ight)}}{3}} ight] + \ln \left( {{e^x} + 3} ight) = 2 \hfill \\ \Leftrightarrow x = 2 \hfill \\ \end{matrix}

  • Câu 7: Vận dụng

    Xét tính đúng sai của các khẳng định

    Vào năm 2014, dân số nước ta khoảng 90,7 triệu người. Giả sử, dân số nước ta sau t năm được xác định bởi hàm số S(t) (đơn vị: triệu người), trong đó tốc độ gia tăng dân số được cho bởi S'(t) = 1,2698e^{0,014t}, với t là số năm kể từ năm 2014, S'(t) tính bằng triệu người / năm.

    a) S(t) là một nguyên hàm của S'(t).Đúng||Sai

    b) S(t) = 90,7e^{0,014t} + 90,7.Sai||Đúng

    c) Theo công thức trên, tốc độ tăng dân số nước ta năm 2034 (làm tròn đến hàng phần mười của triệu người / năm) khoảng 1,7triệu người /năm. Đúng||Sai

    d) Theo công thức trên, dân số nước ta năm 2034 (làm tròn đến hàng đơn vị của triệu người) khoẳng 120triệu người. Đúng||Sai

    Đáp án là:

    Vào năm 2014, dân số nước ta khoảng 90,7 triệu người. Giả sử, dân số nước ta sau t năm được xác định bởi hàm số S(t) (đơn vị: triệu người), trong đó tốc độ gia tăng dân số được cho bởi S'(t) = 1,2698e^{0,014t}, với t là số năm kể từ năm 2014, S'(t) tính bằng triệu người / năm.

    a) S(t) là một nguyên hàm của S'(t).Đúng||Sai

    b) S(t) = 90,7e^{0,014t} + 90,7.Sai||Đúng

    c) Theo công thức trên, tốc độ tăng dân số nước ta năm 2034 (làm tròn đến hàng phần mười của triệu người / năm) khoảng 1,7triệu người /năm. Đúng||Sai

    d) Theo công thức trên, dân số nước ta năm 2034 (làm tròn đến hàng đơn vị của triệu người) khoẳng 120triệu người. Đúng||Sai

    Ta có S(t) là một nguyên hàm của S'(t) và

    \int_{}^{}{S'(t)dt =}\int_{}^{}{1,2698e^{0,014t}dt} = 1,2698\int_{}^{}\left( e^{0,014t} \right)^{t}dt

    = \frac{1,2698e^{0,014t}}{0,014} = 90,7e^{0,014t} + C.

    Vì S(0) = 90,7 nên C = 0. Suy ra S(t) = 90,7e^{0,014t}.

    Tốc độ tăng dân số ở nước ta năm 2034 là:

    S'(20) = 1,2698e^{0,014.20} \approx 1,7 (triệu người/năm).

    Dân số nước ta năm 2034 là: S(20) = 90,7e^{0,014.20} \approx 120 (triệu người).

  • Câu 8: Nhận biết

    Chọn đáp án đúng

    Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị y = f(x), y = g(x), x = a, x = b, (a < b)

    Đáp án đúng: S = \int_{a}^{b}{\left| f(x) - g(x) ight|dx}.

  • Câu 9: Nhận biết

    Tìm khẳng định sai

    Cho hàm số f(x) liên tục trên K và a;b \in K, F(x) là một nguyên hàm của f(x) trên K. Chọn khẳng định sai trong các khẳng định sau?

    Theo định nghĩa tích phân ta có: \int_{a}^{b}{f(x)dx} = F(b) - F(a).

  • Câu 10: Vận dụng

    Xác định giá trị của biểu thức

    Cho F(x) là một nguyên hàm của hàm số f(x) = \frac{2x + 1}{x^{3} + 2x^{3} + x^{2}} trên khoảng (0; + \infty) thỏa mãn F(1) = \frac{1}{2}. Giá trị của biểu thức T = F(1) + F(2) + F(3) + ... + F(2019) bằng:

    Ta có: \int_{}^{}{f(x)dx} = \int_{}^{}{\frac{2x + 1}{x^{2}(x + 1)^{2}}dx} = \int_{}^{}{\left( \frac{1}{x^{2}} - \frac{1}{(x + 1)^{2}} ight)dx}

    Suy ra F(x) = - \frac{1}{x} + \frac{1}{x + 1} + C mà F(1) = \frac{1}{2} \Rightarrow C = 1 .Hay F(x) = - \frac{1}{x} + \frac{1}{x + 1} + 1

    Ta có:

    T = F(1) + F(2) + F(3) + ... + F(2019)

    T = \left( - \frac{1}{1} + \frac{1}{2} + 1 ight) + \left( - \frac{1}{2} + \frac{1}{3} + 1 ight) + \left( - \frac{1}{3} + \frac{1}{4} + 4 ight) + ... + \left( - \frac{1}{2019} + \frac{1}{2020} + 1 ight)

    T = - 1 + \frac{1}{2020} + 2019.1 = 2018 + \frac{1}{2020} = 2018\frac{1}{2020}

  • Câu 11: Thông hiểu

    Tính diện tích hình phẳng D

    Tính diện tích S_{D} của hình phẳng D được giới hạn bởi các đường y = \left| \frac{\ln x}{x} ight|, trục hoành và các đường thẳng x = \frac{1}{e};x = 2?

    Diện tích hình phẳng cần tìm là:

    S_{D} = \int_{\frac{1}{e}}^{2}{\left| \frac{\ln x}{x} ight|dx} = \int_{\frac{1}{e}}^{1}{\left| \frac{\ln x}{x} ight|dx} + \int_{1}^{2}{\left| \frac{\ln x}{x} ight|dx}

    = - \int_{\frac{1}{e}}^{1}{\frac{\ln x}{x}dx} + \int_{1}^{2}{\frac{\ln x}{x}dx}

    = - \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{\frac{1}{e}}^{1} + \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{1}^{2}

    = \frac{1}{2} + \frac{\ln^{2}2}{2} =\frac{1}{2}\left( 1 + \ln^{2}2 ight)

  • Câu 12: Thông hiểu

    Tìm tích phân

    Biết \int_{1}^{2}{\left\lbrack 4f(x) - 2x ightbrack dx} = 1. Khi đó \int_{1}^{2}{f(x)dx} bằng:

    Ta có:

    \int_{1}^{2}{\left\lbrack 4f(x) - 2x ightbrack dx} = 1 \Leftrightarrow 4\int_{1}^{2}{f(x)dx} - 2\int_{1}^{2}{xdx} = 1

    \Leftrightarrow 4\int_{1}^{2}{f(x)dx} - 2\left. \ .x^{2} ight|_{1}^{2} = 1 \Leftrightarrow 4\int_{1}^{2}{f(x)dx} = 4 \Leftrightarrow \int_{1}^{2}{f(x)dx} = 1

  • Câu 13: Vận dụng

    Ghi đáp án vào ô trống

    Trong không gian với hệ tọa độ Oxyz, cho khối cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z + 1)^{2} =25, mặt phẳng (P) có phương trình x + 2y - 2z + 5 = 0 cắt khối cầu (S) thành hai phần. Tính thể tích của phần không chứa tâm của mặt cầu (S).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Trong không gian với hệ tọa độ Oxyz, cho khối cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z + 1)^{2} =25, mặt phẳng (P) có phương trình x + 2y - 2z + 5 = 0 cắt khối cầu (S) thành hai phần. Tính thể tích của phần không chứa tâm của mặt cầu (S).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 14: Nhận biết

    Tính giá trị của biểu thức

    Biết hàm số f(x) = (x - 1)^{2} có nguyên hàm là F(x) = \frac{x^{3}}{a} + bx^{2} + cx + C với a,b,c\mathbb{\in Z}. Tính giá trị biểu thức T = a + b + c.

    Ta có:

    f(x) = (x - 1)^{2} = x^{2} - 2x + 1

    \int_{}^{}{f(x)dx} = \frac{x^{3}}{3} - x^{2} + x + C = F(x)\ \

    Theo bài ra ta có: F(x) = \frac{x^{3}}{a} + bx^{2} + cx + C khi đó:

    \left\{ \begin{matrix} \frac{1}{a} = \frac{1}{3} \\ b = - 1 \\ c = 1 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} a = 3 \\ b = - 1 \\ c = 1 \\ \end{matrix} \right.\ \Rightarrow T = 3 - 1 + 1 = 3

    Vậy đáp án cần tìm là: F(x) = \frac{x^{4}}{4} - \frac{x^{3}}{3} + x^{2} - x + \frac{49}{12}

  • Câu 15: Thông hiểu

    Tính vận tốc dự định của người đi xe đạp

    Một người đi xe đạp dự định trong buổi sáng đi hết quãng đường 60 km. Khi đi được \frac{1}{2} quãng đường, anh ta thấy vận tốc của mình chỉ bằng \frac{2}{3} vận tốc dự định, anh ta bèn đạp nhanh hơn vận tốc dự định 3km/h, đến nơi anh ta vẫn chậm mất 45 phút. Hỏi vận tốc dự định của người đi xe đạp là bao nhiêu?

    Vận tốc dự định là v(km/h).

    Thời gian đi nửa quãng đường đầu t_{1} = \frac{30}{\frac{2}{3}v} = \frac{45}{v}(h).

    Thời gian đi nửa quãng đường sau t_{2} = \frac{30}{v + 3}(h).

    Ta có phương trình

    t_{1} + t_{2} = \frac{60}{v} - 0,75 \Leftrightarrow \frac{45}{v} + \frac{30}{v + 3} = \frac{60}{v} + 0,75

    Giải phương trình suy ra: v = 12 km/h.

  • Câu 16: Nhận biết

    Chọn đáp án đúng

    Cho hàm số f(x) = x^{3} - x^{2} + 2x - 1. Gọi F(x) là một nguyên hàm của f(x), biết rằng F(1) = 4 thì:

    Ta có:

    \int_{}^{}{f(x)dx} = \frac{x^{4}}{4} - \frac{x^{3}}{3} + x^{2} - x + C = F(x)

    Theo bài ra ta có: F(1) = 4

    \Leftrightarrow \frac{1^{4}}{4} - \frac{1^{3}}{3} + 1^{2} - 1 + C = 4 \Leftrightarrow C = \frac{49}{12}

    Vậy đáp án cần tìm là: F(x) = \frac{x^{4}}{4} - \frac{x^{3}}{3} + x^{2} - x + \frac{49}{12}

  • Câu 17: Vận dụng cao

    Xác định thể tích V

    Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 như hình vẽ:

    Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x;( - 1 \leq x \leq 1)thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó.?

    Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x;( - 1 \leq x \leq 1) thì được thiết diện là một tam giác đều có cạnh bằng 2\sqrt{1 - x^{2}}

    Do đó, diện tích của thiết diện: S(x) =\frac{\left( 2\sqrt{1 - x^{2}} ight)^{2}\sqrt{3}}{4} = \sqrt{3}\left(1 - x^{2} ight)

    V = \int_{- 1}^{1}{S(x)dx} = \int_{-1}^{1}{\left\lbrack \sqrt{3}\left( 1 - x^{2} ight) ightbrackdx}

    = \sqrt{3}\left. \ \left( x -\frac{x^{3}}{3} ight) ight|_{- 1}^{1} =\frac{4\sqrt{3}}{3}

  • Câu 18: Nhận biết

    Xác định thể tích vật thể

    Tính thể tích của vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 \leq x \leq 3) là một hình chữ nhật có hai kích thước là x và 2\sqrt{9 - x^{2}}.

    Ta có:

    V = \int_{0}^{3}{2x\sqrt{9 - x^{2}}dx} = 18

  • Câu 19: Nhận biết

    Chọn đáp án đúng

    Cho hàm số f(x) có đạo hàm f'(x) liên tục trên \lbrack a;bbrack; f(b) = 5;\int_{a}^{b}{f'(x)dx} = 3\sqrt{5}. Tính giá trị f(a)?

    Ta có: \int_{a}^{b}{f'(x)dx} = 3\sqrt{5} \Leftrightarrow f(b) - f(a) = 3\sqrt{5}

    \Leftrightarrow f(a) = f(b) - 3\sqrt{5} = \sqrt{5}\left( \sqrt{5} - 3 ight)

  • Câu 20: Nhận biết

    Chọn đáp án thích hợp

    Tích phân I = \int_{0}^{1}\left( ax^{2} + bx \right)dx có giá trị là:

    Tích phân I = \int_{0}^{1}\left( ax^{2} + bx ight)dx có giá trị là:

    I = \int_{0}^{1}\left( ax^{2} + bx ight)dx = \left. \ \left( \frac{a}{3}x^{3} + \frac{b}{2}x^{2} ight) ight|_{0}^{1} = \frac{a}{3} + \frac{b}{2}.

    Đáp án đúng là I = \frac{a}{3} + \frac{b}{2}.

  • Câu 21: Vận dụng

    Chọn đáp án đúng

    Với phương pháp đổi biến số (x \rightarrow t), nguyên hàm I = \int_{}^{}{\frac{1}{\sqrt{- x^{2} + 2x + 3}}dx} bằng:

    Ta biến đổi: I = \int_{}^{}{\frac{1}{\sqrt{4 - (x - 1)^{2}}}dx}.

    Đặt x - 1 = 2sint,t \in \left\lbrack - \frac{\pi}{2},\frac{\pi}{2} \right\rbrack \Rightarrow dx = 2costdt.

    \Rightarrow I = \int_{}^{}{dt = t + C}.

  • Câu 22: Thông hiểu

    Tính thể tích khối tròn xoay

    Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD với A( - 1;2), B(5;5), C(5;0), D( - 1;0). Quay hình thang ABCD xung quanh trục Ox thì thể tích khối tròn xoay tạo thành bằng bao nhiêu?

    Hình vẽ minh họa

    Phương trình đường thẳng AB là:

    \frac{x + 1}{5 + 1} = \frac{y - 2}{5 - 2} \Leftrightarrow y = \frac{1}{2}x + \frac{5}{2}

    Thể tích khối tròn xoay là:

    V = \pi\int_{- 1}^{5}{f^{2}(x)dx} = \pi\int_{- 1}^{5}{\left( \frac{1}{2}x + \frac{5}{2} ight)^{2}dx} = 78\pi

  • Câu 23: Thông hiểu

    Chọn đáp án đúng

    Hãy xác định hàm số f(x) từ đẳng thức: x^{2} + xy + C = \int_{}^{}{f(y)dy}

    Ta có: \left( x^{2} + xy \right)' = x + C

    Vậy f(x) = x.

  • Câu 24: Vận dụng

    Tính tích phân

    Cho hai hàm số f(x) = ax^{3} + bx + c;g(x) = bx^{3} + ax + c;(a > 0) có đồ thị như hình vẽ:

    Gọi S_{1};S_{2} là diện tích hình phẳng được gạch trong hình vẽ. Khi S_{1} + S_{2} = 3 thì \int_{0}^{1}{f(x)dx} bằng bao nhiêu?

    Phương trình hoành độ giao điểm

    (a - b)x^{3} + (b - a)x = 0

    \Leftrightarrow (a - b)\left( x^{3} - x ight) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 1 \\ x = 0 \\ \end{matrix} ight.

    Ký hiệu S_{3} là diện tích hình phẳng như hình vẽ:

    Ta có:

    S_{1} = \int_{- 1}^{0}{\left\lbrack f(x) - g(x) ightbrack dx} = (a - b)\int_{- 1}^{0}{\left( x^{3} - x ight)dx} = \frac{1}{4}(a - b)

    S_{2} = - \int_{- 1}^{0}{g(x)dx} = - \int_{- 1}^{0}{\left( bx^{3} + ax + c ight)dx} = - \left( \frac{b}{4} + \frac{a}{2} + c ight)

    Vì vậy S_{1} + S_{2} = 3 \Leftrightarrow \frac{1}{4}(a - b) - \left( \frac{b}{4} + \frac{a}{2} + c ight) = 3

    \Leftrightarrow a + 2b + 4c = - 12

    \Rightarrow \int_{0}^{1}{f(x)dx} = \int_{0}^{1}{\left( ax^{3} + bx + c ight)dx} = \frac{a}{4} + \frac{b}{2} + c = \frac{a + 2b + 4c}{4} = - 3

  • Câu 25: Nhận biết

    Chọn đáp án đúng

    Cho \int_{}^{}{f(x)dx} = \frac{x^{4}}{4} - \frac{x^{3}}{3} + 2020 + C. Khi đó \int_{}^{}{f(3x)dx} là:

    Ta có: \int_{}^{}{f(x)dx} = \frac{x^{4}}{4} - \frac{x^{3}}{3} + 2020 + C

    Khi đó \int_{}^{}{f(3x)dx} = \frac{27x^{4}}{4} - 3x^{3} + \frac{2020}{3} + C

  • Câu 26: Thông hiểu

    Hàm số f(x) = x^3 + 3x - 2 có một nguyên hàm F(x)

    Hàm số f\left( x ight) = {x^3} + 3x - 2 có một nguyên hàm F(x). Biết đồ thị hàm số y = F(x) đi qua điểm B(2; 10). Giá trị F(-2) là:

     F\left( x ight) = \int {\left( {{x^3} + 3x - 2} ight)dx = \frac{{{x^4}}}{4} + \frac{{3{x^2}}}{2} - 2x + C}

    Hàm số đi qua B(2; 10) => \frac{{{2^4}}}{4} + \frac{{{{3.2}^2}}}{2} - 2.2 + C = 10 \Rightarrow C = 4

    => F\left( x ight) = \frac{{{x^4}}}{4} + \frac{{3{x^2}}}{2} - 2x + 4

    => F\left( { - 2} ight) = \frac{{{{\left( { - 2} ight)}^4}}}{4} + \frac{{3.{{\left( { - 2} ight)}^2}}}{2} - 2\left( { - 2} ight) + 4 = 6

  • Câu 27: Thông hiểu

    Chọn phương án thích hợp

    Tích phân I = \int_{0}^{\frac{\pi}{2}}{\left( \cos x - 1 \right)cos^{2}x}dx có giá trị là:

    Ta biến đổi: I = \int_{0}^{\frac{\pi}{2}}{\left( \cos x - 1 ight)cos^{2}x}dx

    = \int_{0}^{\frac{\pi}{2}}{\cos x\left( 1 - sin^{2}x ight)}dx - \int_{0}^{\frac{\pi}{2}}{cos^{2}x}dx

    = \left. \ \left( t - \frac{t^{3}}{3} ight) ight|_{0}^{1} - \frac{1}{2}\left. \ \left( x + \frac{1}{2}sin2x ight) ight|_{0}^{\frac{\pi}{2}} = \frac{2}{3} - \frac{\pi}{4}, với t = \sin x.

    Đáp án đúng là I = - \frac{\pi }{4} + \frac{2}{3}.

  • Câu 28: Vận dụng cao

    Chọn kết luận đúng

    Cho hai hàm số y = f(x) và y = g(x) không âm, có đạo hàm trên đoạn [1; 4] và thỏa mãn các hệ thức f\left( 1 ight) + g\left( 1 ight) = 4;g\left( x ight) = - xf'\left( x ight);f\left( x ight) = - xg'\left( x ight). Kết luận nào sau đây đúng?

    Ta có:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {g\left( x ight) = - xf'\left( x ight)} \\ {f\left( x ight) = - xg'\left( x ight)} \end{array}} ight. \hfill \\ \Rightarrow f\left( x ight) + g\left( x ight) = - x\left[ {f'\left( x ight) + g'\left( x ight)} ight] \hfill \\ \Rightarrow \dfrac{{f'\left( x ight) + g'\left( x ight)}}{{f\left( x ight) + g\left( x ight)}} = \dfrac{{ - 1}}{x} \hfill \\ \end{matrix}

    \begin{matrix} \Rightarrow \int\limits_1^4 {\dfrac{{f'\left( x ight) + g'\left( x ight)}}{{f\left( x ight) + g\left( x ight)}}dx = \int\limits_1^4 {\dfrac{{ - 1}}{x}dx} } \hfill \\ \Leftrightarrow \int\limits_1^4 {\dfrac{{d\left[ {f\left( x ight) + g\left( x ight)} ight]}}{{f\left( x ight) + g\left( x ight)}} = } \left. {\ln \left| x ight|} ight|_1^4 = - \ln 4 \hfill \\ \Rightarrow \ln \left| {f\left( x ight) + g\left( x ight)} ight|_1^4 = - \ln 4 \hfill \\ \Rightarrow \ln \left| {f\left( 4 ight) + g\left( 4 ight)} ight| - \ln \left| {f\left( 1 ight) + g\left( 1 ight)} ight| = - \ln 4 \hfill \\ \Rightarrow \ln \left| {f\left( 4 ight) + g\left( 4 ight)} ight| = 0 \hfill \\ \Rightarrow f\left( 4 ight) + g\left( 4 ight) = 1 \hfill \\ \end{matrix}

     

  • Câu 29: Thông hiểu

    Tính giá trị biểu thức

    Cho hàm số f(x) có đạo hàm với mọi x\mathbb{\in R} và f'(x) = 2x + 1. Giá trị của f(2) - f(1) bằng:

    Ta có:

    f'(x) = 2x + 1 \Rightarrow\int_{}^{}{f'(x)dx = \int_{}^{}{(2x + 1)dx}}

    = x^{2} + x + C \Rightarrow \existsC_{1}\mathbb{\in R}:f(x) = x^{2} + x + C

    \Rightarrow f(2) - f(1) = 2^{2} + 2 +C_{1} - \left( 1^{2} + 1 + C_{1} ight) = 4

  • Câu 30: Thông hiểu

    Xác định giá trị tích phân

    Cho hàm số y = f(x) có đạo hàm liên tục trên \mathbb{R} và có đồ thị như hình vẽ:

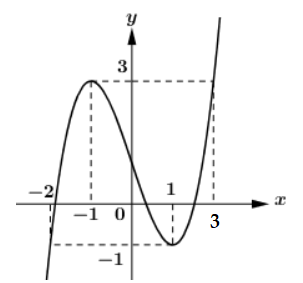
    Tích phân

    Tính tích phân I = \int_{1}^{2}{f'(2x - 1)dx}?

    Ta có:

    I = \int_{1}^{2}{f'(2x - 1)dx} = \frac{1}{2}\int_{1}^{2}{f'(2x - 1)d(2x - 1)}

    = \frac{1}{2}\left. \ f(2x - 1)ight|_{1}^{2} = \frac{1}{2}\left\lbrack f(3) - f(1) ightbrack =2

  • Câu 31: Thông hiểu

    Tính vận tốc của vật

    Một vật chuyển động với vận tốc v(t)(m/s)có gia tốc v'(t) = \frac{3}{t + 1}\left( m/s^{2} ight). Vận tốc ban đầu của vật là 6m/s. Tính vận tốc của vật sau 10 giây, (làm tròn kết quả đến hàng đơn vị).

    Vận tốc của vật là:v(t) = \int_{}^{}{v'(t)dt} = \int_{}^{}{\frac{3}{t + 1}dt} = 3ln(t + 1) + C

    Do vận tốc ban đầu của vật là 6m/s

    \Rightarrow v_{(t = 0)} = 6 \Rightarrow 3ln1 + C = 6 \Rightarrow C = 6

    Vận tốc của vật sau 10s là v(10) = 3ln11 + 6 \approx 13m/s

  • Câu 32: Thông hiểu

    Chọn đáp án đúng

    Tìm một nguyên hàm F(x) của hàm số f(x) = ax + \frac{b}{x^{2}};(x eq 0), biết rằng F( - 1) = 1;F(1) = 4;f(1) = 0?

    Ta có: F(x) = \int_{}^{}{\left( ax + \frac{b}{x^{2}} ight)dx = \frac{ax^{2}}{2} - \frac{b}{x} + c}

    Theo bài ra ta có:

    F( - 1) = 1;F(1) = 4;f(1) = 0

    \Rightarrow \left\{ \begin{matrix}\dfrac{a}{2} + b + c = 1 \\\dfrac{a}{2} - b + c = 4 \\a + b = 0 \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}a = \dfrac{3}{2} \\b = - \dfrac{3}{2} \\c = \dfrac{7}{4} \\\end{matrix} ight.. Vậy F(x) = \frac{3x^{2}}{4} + \frac{3}{2x} + \frac{7}{4}.

  • Câu 33: Thông hiểu

    Chọn đáp án chính xác

    Biết rằng A = \int_{}^{}\frac{\cos x}{\sin x + \cos x}dx;B = \int_{}^{}\frac{\sin x}{\sin x + \cos x}dx. Xác định T = 4B - 2A?

    Ta có: \left\{ \begin{gathered} A + B = \int 1 dx = x + {C_1} \hfill \\ A - B = \int {\frac{{\cos x - \sin x}}{{\sin x + \cos x}}} dx = \ln \left| {\sin x + \cos x} ight| + {C_2} \hfill \\ \end{gathered} ight.

    Do đó:\left\{ \begin{gathered} A = \frac{{x + \ln \left| {\sin x + \cos x} ight|}}{2} + \frac{{{C_1} + {C_2}}}{2} \hfill \\ B = \frac{{x - \ln \left| {\sin x + \cos x} ight|}}{2} + \frac{{{C_1} - {C_2}}}{2} \hfill \\ \end{gathered} ight.

    \Rightarrow T = 4B - 2A = x - 3\ln\left|\sin x + \cos x ight| + C

  • Câu 34: Nhận biết

    Tính tích phân I

    Giá trị tích phân I = \int_{1}^{2}{\frac{1}{x^{6}}dx} bằng:

    Ta có:

    I = \int_{1}^{2}{\frac{1}{x^{6}}dx} = \int_{1}^{2}{x^{- 6}dx} = \left. \ \frac{x^{- 5}}{- 5} ight|_{1}^{2} = \frac{31}{125}

  • Câu 35: Vận dụng

    Chọn đáp án đúng

    Tích phân I = \int_{\frac{\pi}{3}}^{\frac{\pi}{6}}{\frac{\sin^{3}x}{\sqrt{\cos x}}dx} có giá trị là:

    Ta nhận thấy: \left( \cos x ight)' = - \sin x. Ta dùng đổi biến số.

    Đặt t = \cos x \Rightarrow dt = - \sin xdx.

    Đổi cận\left\{ \begin{matrix} x = \dfrac{\pi}{3} \Rightarrow t = \dfrac{1}{2} \\ x = \dfrac{\pi}{6} \Rightarrow t = \dfrac{\sqrt{3}}{2} \\ \end{matrix} ight..

    I = \int_{\dfrac{\pi}{3}}^{\dfrac{\pi}{2}}{\dfrac{\sin^{3}x}{\sqrt{\cos x}}dx} = \int_{\dfrac{\pi}{3}}^{\dfrac{\pi}{2}}{\dfrac{\left( 1 - \cos^{2}x ight)\sin x}{\sqrt{\cos x}}dx}

    \Rightarrow I = \int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}{\frac{t^{2} - 1}{\sqrt{t}}dt} = {\int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}{\left( t^{\frac{3}{2}} - t^{- \frac{1}{2}} ight)dx }}

    \left. { = \left( {\frac{2}{5}{t^{\frac{5}{2}}} - 2{t^{\frac{1}{2}}}} ight)} ight|_{\frac{1}{2}}^{\frac{{\sqrt 3 }}{2}} = \frac{{19 - 17\sqrt[4]{3}}}{{\sqrt 2 }}

    Tích phân I = \int_{\frac{\pi}{3}}^{\frac{\pi}{6}}{\frac{sin^{3}x}{\sqrt{\cos x}}dx} có giá trị là: I = \frac{19 - 17\sqrt[4]{3}}{\sqrt{2}}.

  • Câu 36: Nhận biết

    Chọn đáp án đúng

    Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox : y = 2x - x^{2},\ y = 0,\ x = 0,\ x = 2.

    Thể tích khối tròn xoay V = \pi\int_{0}^{2}{\left( 2x - x^{2} \right)^{2}dx} = \frac{16\pi}{15}.

  • Câu 37: Vận dụng cao

    Tính quãng đường người chạy được

    Một người chạy trong thời gian 1 giờ, vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường thẳng parabol với I\left( \frac{1}{2};8 \right) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy

    Ta tìm được phương trình của parabol là

    (P):v(t) = - 32t^{2} + 32t

    Quãng đường s mà người đó chạy được trong khoảng thời gian 0,75 (h) là:

    s = \int_{0}^{0,75}{\left( - 32t^{2} + 32t ight)dt}

    = \left( - \frac{32}{3}t^{3} + 16t^{2} ight)|_{0}^{0,75} = 4,5(km)

  • Câu 38: Thông hiểu

    Tính diện tích hình phẳng

    Diện tích hình phẳng giới hạn bởi nhánh đường cong y = x^{2} với x \geq 0, đường thẳng y = 2 - x và trục hoành bằng

    Xét phương trình hoành độ giao điểm:

    x^{2} = 2 - x \Leftrightarrow x^{2} + x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2(ktm) \\ \end{matrix} ight.

    Ta có \Rightarrow S = \int_{0}^{1}{\left| x^{2} - (2 - x) ight|d_{x}} = \frac{7}{6}

  • Câu 39: Nhận biết

    Tìm quãng đường chuyển động

    Một vật chuyển động chậm dần với vận tốc v(t) = 150 - 15t(m/s). Hỏi rằng trong 5s trước khi dừng hẳn vật di chuyển được bao nhiêu mét?

    Khi dừng hẳn v(t) = 150 - 15t = 0 \Rightarrow t = 10(s)

    Khi đó trong 5s trước khi dừng hẳn vật di chuyển được:

    S = \int_{0}^{10}{v(t)dt} = \int_{0}^{10}{(150 - 15t)dt} = \frac{375}{2}m.

  • Câu 40: Nhận biết

    Tìm câu sai

    Câu nào sau đây sai?

    Câu sai cần tìm là: Nếu F'(t) = f(t) thì F^{/}\left( u(x) \right) = f\left( u(x) \right).

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 4 Nguyên hàm và tích phân Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
21 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề kiểm tra 45 phút Chương 4 Nguyên hàm và tích phân
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 12 - Kết nối tri thức
Xem thêm