Đề kiểm tra giữa học kì 1 môn Toán lớp 8 năm học 2022 - 2023 Đề 2

Đề kiểm tra giữa học kỳ 1 môn Toán lớp 8 có đáp án

Đề thi giữa kì 1 môn Toán lớp 8 có đáp án

Đề thi Toán 8 giữa kì 1 số 1
Đề thi Toán 8 giữa kì 1 số 2
Đáp án đề thi Toán 8 giữa kì 1 số 2

Đề thi giữa học kì môn Toán lớp 8 năm học 2022 - 2023 được VnDoc biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học THCS. Đề thi Toán giữa kì 1 bao gồm cả trắc nghiệm và tự luận, là tài liệu hữu ích cho các em ôn luyện, đồng thời cũng là tài liệu hay cho thầy cô tham khảo ra đề. Mời các bạn tải về để xem toàn bộ đề và đáp án.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 8, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 8 sau: Nhóm Tài liệu học tập lớp 8. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đề thi Toán 8 giữa kì 1 số 1

I. Trắc nghiệm:(3.0 điểm) Hãy khoanh tròn vào đáp án đúng.

Câu 1. Kết quả của phép nhân x( x – 3) là:

A. x²– 3x	C. x²+ 3x
B. x² + 3x	D. x² - 3

Câu 2. Chọn đẳng thức đúng trong các đẳng thức sau:

A. (x - y)² = x²– 2xy - y²	C. x² - y² = (x – y)(x - y)
B. (x + y)³ = x³– 3x²y + 3xy²– y³	D. (x + y)³ = x³+ 3x²y + 3xy²+ y³

Câu 3. Giá trị của biểu thức x³ + 3x² + 3x + 1 tại x = 2 là:

A. 27

B. -27

C. 8

D. 9

Câu 4.Kết quả của phép tính ( x – 2)(x – 3 ) là :

A. x²– 5x + 6

B. x² + 5x + 6

C. x² – x + 6

D. x² + x + 6

Câu 5. Phân tích đa thức 5x²– 2x thành nhân tử ta được kết quả là:

A. 5(x – 2)

B.5x(3x – 2)

C. x(5x – 2)

D. 5x(x - 2)

Câu 6.Tứ giác ABCD có $\hat{A}$ $\hat{A}$ = 120⁰; $\hat{B}$ $\hat{B}$= 80⁰ ; $\hat{C}$ $\hat{C}$ = 100⁰ thì:

A. $\hat{D}$ $\hat{D}$= 150⁰ ;

B. $\hat{D}$ $\hat{D}$ = 90⁰ ;

C. $\hat{D}$ $\hat{D}$ = 40⁰ ;

D. $\hat{D}$ $\hat{D}$ = 60⁰

II. Phần tự luận (7.0 điểm)

Câu 7. (1.5 điểm)Phân tích các đa thức sau thành nhân tử.

a) x³+ 3x

b) x²+ 2xy –4 + y²

Câu 8 . (1.5 điểm) Tìm x biết :

a) x²– 9 = 0

b) x(x - 5) + x - 5 = 0

Câu 9.(1,0điểm) Sắp xếp các đa thức theo luỹ thừa giảm dần của biến rồi làm tính chia :

(2x³ + 5x + 4x² + 3) : (x + 1)

Câu 10. ( 2.0 điểm) Cho tam giác MNP. Gọi E,F,I theo thứ tự là trung điểm của các cạnh MN, MP, NP. Biết MP = 16 cm

a) Tính EI?

b)Chứng minh tứ giác MEIF là hình bình hành.

Câu 11 . (1.0 điểm) Cho biểu thức P = x² - 3x + 7. Hãy tìm giá trị nhỏ nhất của P

Xem đáp án trong file tải về

Đề thi Toán 8 giữa kì 1 số 2

Câu 1 (2 điểm) Phân tích đa thức thành nhân tử

$a. 6{{x}^{2}}-6xy-4x+4y$ $a. 6{{x}^{2}}-6xy-4x+4y$	$b. {{x}^{3}}+10{{x}^{2}}+25x-x{{y}^{2}}$ $b. {{x}^{3}}+10{{x}^{2}}+25x-x{{y}^{2}}$
$c. {{x}^{2}}+x-6$ $c. {{x}^{2}}+x-6$	$d. 2{{x}^{2}}+4x-16$ $d. 2{{x}^{2}}+4x-16$

Câu 2 (2 điểm) Tìm giá trị của x, biết:

$a. {{x}^{3}}-16x=0$ $a. {{x}^{3}}-16x=0$
$b. {{\left( 2x+1 \right)}^{2}}-{{\left( x-1 \right)}^{2}}=0$ $b. {{\left( 2x+1 \right)}^{2}}-{{\left( x-1 \right)}^{2}}=0$
Câu 3 (2 điểm) Chứng minh biểu thức sau không phụ thuộc vào x

$a. A=\left( 2x-1 \right)\left( 4{{x}^{2}}+2x+1 \right)-\left( 2x+1 \right)\left( 4{{x}^{2}}-2x+1 \right)$ $a. A=\left( 2x-1 \right)\left( 4{{x}^{2}}+2x+1 \right)-\left( 2x+1 \right)\left( 4{{x}^{2}}-2x+1 \right)$

$b. B=x\left( 2x+1 \right)-{{x}^{2}}\left( x+2 \right)+{{x}^{3}}-x+5$ $b. B=x\left( 2x+1 \right)-{{x}^{2}}\left( x+2 \right)+{{x}^{3}}-x+5$

Câu 4 (1 điểm) Tính giá trị nhỏ nhất của biểu thức _{$P={{x}^{2}}-2xy+6{{y}^{2}}-12x+2y+45$}

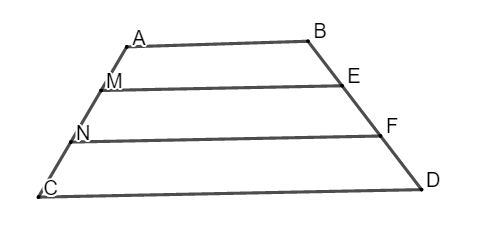
Câu 5 (2 điểm) Cho hình thang ABDC (AB // CD). Trên cạnh AD lấy điểm M và N sao cho AM = MN = NC. Từ M và N kẻ các đường thẳng song song với hai đáy cắt BC theo thứ tự E và F. Chứng minh rằng:

a. BE = EF = FD

b. Cho CD = 8cm, ME = 6cm. Tính độ dài AB và FN

Câu 6 (0,5 điểm) Cho x, y, z là các số dương. Tìm giá trị nhỏ nhất của:

$P=\left( x+y+z \right)\left( \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right)$ $P=\left( x+y+z \right)\left( \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right)$

Đáp án đề thi Toán 8 giữa kì 1 số 2

Câu 1:

a. $6{{x}^{2}}-6xy-4x+4y=6x\left( x-y \right)-4\left( x-y \right)=\left( x-y \right)\left( 6x-4 \right)$ $6{{x}^{2}}-6xy-4x+4y=6x\left( x-y \right)-4\left( x-y \right)=\left( x-y \right)\left( 6x-4 \right)$

b.

$x^3+10x^2+25x-xy^2=x\left(x^2+10x+25-y^2\right)=x\left[\left(x+5\right)^2-y^2\right]=x\left(x+5-y\right)\left(x+5+y\right)$ $x^3+10x^2+25x-xy^2=x\left(x^2+10x+25-y^2\right)=x\left[\left(x+5\right)^2-y^2\right]=x\left(x+5-y\right)\left(x+5+y\right)$

c. ${{x}^{2}}+x-6={{x}^{2}}-2x+3x-6=x\left( x-2 \right)+3\left( x-2 \right)=\left( x-2 \right)\left( x+3 \right)$ ${{x}^{2}}+x-6={{x}^{2}}-2x+3x-6=x\left( x-2 \right)+3\left( x-2 \right)=\left( x-2 \right)\left( x+3 \right)$

d.

$\begin{align} & 2{{x}^{2}}+4x-16=2\left( {{x}^{2}}+2x-8 \right)=2\left( {{x}^{2}}+2x+1-9 \right) \\ & =2\left[ {{\left( x+1 \right)}^{2}}-9 \right]=2\left( x+1-3 \right)\left( x+1+3 \right)=2\left( x-2 \right)\left( x+4 \right) \\ \end{align}$ $\begin{align} & 2{{x}^{2}}+4x-16=2\left( {{x}^{2}}+2x-8 \right)=2\left( {{x}^{2}}+2x+1-9 \right) \\ & =2\left[ {{\left( x+1 \right)}^{2}}-9 \right]=2\left( x+1-3 \right)\left( x+1+3 \right)=2\left( x-2 \right)\left( x+4 \right) \\ \end{align}$

Câu 2:

a.

$\begin{align} & {{x}^{3}}-16x=0 \\ & \Leftrightarrow x\left( {{x}^{2}}-16 \right)=0 \\ & \Leftrightarrow x\left( x-4 \right)\left( x+4 \right)=0 \\ \end{align}$ $\begin{align} & {{x}^{3}}-16x=0 \\ & \Leftrightarrow x\left( {{x}^{2}}-16 \right)=0 \\ & \Leftrightarrow x\left( x-4 \right)\left( x+4 \right)=0 \\ \end{align}$

Suy ra x = 0, x = 4, x = -4

b.

$\begin{align} & {{\left( 2x+1 \right)}^{2}}-{{\left( x-1 \right)}^{2}}=0 \\ & \Leftrightarrow \left( 2x+1-x+1 \right)\left( 2x+1+x-1 \right)=0 \\ & \Leftrightarrow \left( x+2 \right)\left( 3x \right)=0 \\ \end{align}$ $\begin{align} & {{\left( 2x+1 \right)}^{2}}-{{\left( x-1 \right)}^{2}}=0 \\ & \Leftrightarrow \left( 2x+1-x+1 \right)\left( 2x+1+x-1 \right)=0 \\ & \Leftrightarrow \left( x+2 \right)\left( 3x \right)=0 \\ \end{align}$

Suy ra x = 0 hoặc x = -2

Câu 3:

a.

$\begin{align} & A=\left( 2x-1 \right)\left( 4{{x}^{2}}+2x+1 \right)-\left( 2x+1 \right)\left( 4{{x}^{2}}-2x+1 \right) \\ & A={{\left( 2x \right)}^{3}}-1-\left[ {{\left( 2x \right)}^{3}}+1 \right] \\ & A=8{{x}^{3}}-1-8{{x}^{3}}-1 \\ & A=-2 \\ \end{align}$ $\begin{align} & A=\left( 2x-1 \right)\left( 4{{x}^{2}}+2x+1 \right)-\left( 2x+1 \right)\left( 4{{x}^{2}}-2x+1 \right) \\ & A={{\left( 2x \right)}^{3}}-1-\left[ {{\left( 2x \right)}^{3}}+1 \right] \\ & A=8{{x}^{3}}-1-8{{x}^{3}}-1 \\ & A=-2 \\ \end{align}$

Vậy biểu thức không phụ thuộc vào x

b.

$\begin{align} & B=x\left( 2x+1 \right)-{{x}^{2}}\left( x+2 \right)+{{x}^{3}}-x+5 \\ & B=2{{x}^{2}}+x-{{x}^{3}}-2{{x}^{2}}+{{x}^{3}}-x+5 \\ & B=5 \\ \end{align}$ $\begin{align} & B=x\left( 2x+1 \right)-{{x}^{2}}\left( x+2 \right)+{{x}^{3}}-x+5 \\ & B=2{{x}^{2}}+x-{{x}^{3}}-2{{x}^{2}}+{{x}^{3}}-x+5 \\ & B=5 \\ \end{align}$

Vậy biểu thức không phụ thuộc vào x

Câu 4:

$\begin{align} & P={{x}^{2}}-2xy+6{{y}^{2}}-12x+2y+45 \\ & P={{x}^{2}}+{{y}^{2}}+36-2xy-12x+12y+5{{y}^{2}}-10y+5+4 \\ & P={{\left( x-y-6 \right)}^{2}}+5{{\left( y-1 \right)}^{2}}+4 \\ \end{align}$ $\begin{align} & P={{x}^{2}}-2xy+6{{y}^{2}}-12x+2y+45 \\ & P={{x}^{2}}+{{y}^{2}}+36-2xy-12x+12y+5{{y}^{2}}-10y+5+4 \\ & P={{\left( x-y-6 \right)}^{2}}+5{{\left( y-1 \right)}^{2}}+4 \\ \end{align}$

Do _{$\left\{ \begin{matrix} {{\left( x-y-6 \right)}^{2}}\ge 0 \\ {{\left( y-1 \right)}^{2}}\ge 0 \\ \end{matrix} \right.,\forall x,y$} $\Rightarrow P\ge 4$ $\Rightarrow P\ge 4$

Vậy giá trị nhỏ nhất của biểu thức P là 4 khi và chỉ khi x = 7 và y = 1

Câu 5:

Đề kiểm tra giữa học kì 1 môn Toán lớp 8 năm học 2020 - 2021 Đề 2

a. Ta có ABCD là hình thang AB // CD

Ta có AB // CD, FN // CD suy ra AB // NF

Vậy ABFN là hình thang

Xét hình thang ABFN có ME // NF, ME = NF nên ME là đường trung bình của hình thang ABFN

Suy ra BE = EF

Xét tương tự với hình thang MEDC ta suy ra EF = FD

Ta có điều phải chứng minh

b. Theo chứng minh trên ta có

$NF=\frac{1}{2}\left( ME+CD \right)=\frac{1}{2}\left( 6+8 \right)=7cm$ $NF=\frac{1}{2}\left( ME+CD \right)=\frac{1}{2}\left( 6+8 \right)=7cm$

Ta lại có: $ME=\frac{1}{2}\left( AB+NF \right)\Rightarrow AB=2ME-NF=2.6-7=5cm$ $ME=\frac{1}{2}\left( AB+NF \right)\Rightarrow AB=2ME-NF=2.6-7=5cm$

Câu 6:

$P=\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1$ $P=\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1$

$=3+\left(\frac{x}{y}+\frac{y}{x}\right)+\left(\frac{x}{z}+\frac{z}{x}\right)+\left(\frac{y}{z}+\frac{z}{y}\right)$ $=3+\left(\frac{x}{y}+\frac{y}{x}\right)+\left(\frac{x}{z}+\frac{z}{x}\right)+\left(\frac{y}{z}+\frac{z}{y}\right)$

Mặt khác $\left( \frac{x}{y}+\frac{y}{x} \right)\ge 2$ $\left( \frac{x}{y}+\frac{y}{x} \right)\ge 2$ với mọi số dương x, y nên

$P=3+2+2+2=9$

Vậy giá trị nhỏ nhất của P là 9 khi x = y = z

Mời các bạn tải tài liệu miễn phí tham khảo hướng dẫn giải chi tiết!

-------------------------------------------------

Trên đây là VnDoc.com giới thiệu tới quý thầy cô và bạn đọc Đề kiểm tra giữa học kì 1 môn Toán 8 có đáp án. Ngoài ra VnDoc mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Toán lớp 8, Tiếng anh lớp 8, Vật lí lớp 8, Ngữ văn lớp 8,...

Chia sẻ, đánh giá bài viết

38

11.449

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Thị Huê
Nhóm:
VnDoc.com
Ngày: 18/10/2022

Tải về

Chọn file muốn tải về: