Đề ôn tập hè lớp 7 lên lớp 8 môn Toán năm 2019 - 2020 - Đề số 2

Đề ôn tập hè lớp 7 lên lớp 8 - Đề số 2 được VnDoc biên soạn bao gồm bài tập ôn hè môn Toán dành cho các em học sinh lớp 7 luyện tập, cùng cố lại kiến thức, nhằm chuẩn bị nền tảng vững chắc khi lên lớp 8, chuẩn bị kiến thức cho năm học mới. Chúc các em học tốt.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. Đề ôn tập hè lớp 7 lên lớp 8 môn Toán – Đề số 2

Bài 1: Thực hiện phép tính (tính nhanh nếu có thể)

a, \(\frac{{ - 3}}{4} - \left( {7\frac{3}{8} - \frac{{11}}{{24}}} \right)\)	b, \(\frac{{ - 1}}{2}.12\frac{4}{5} + \frac{{13}}{5} + 2\frac{4}{5}\)
c, \(\left( {\frac{{ - 4}}{{15}} - \frac{{13}}{7}} \right).\frac{3}{5} + \left( {1\frac{6}{7} + \frac{4}{{15}}} \right).\frac{3}{5}\)	d, \(\frac{{\frac{1}{5} - \frac{1}{7} - \frac{1}{3}}}{{\frac{2}{5} - \frac{2}{7} - \frac{2}{3}}} + \frac{4}{{16}} - {\left( { - \frac{5}{4}} \right)^2}\)

Bài 2: Tìm x, biết:

a, \(\left| {3x - 14} \right| - \left| {x + 2} \right| = 0\)	b, \({\left( {x + \frac{4}{7}} \right)^3} = - \left( { - 27} \right)\)
c, \({5^{x + 4}}{.5^3} = 625\)	d, \(\frac{{x + 1}}{3} = \frac{{4x + 7}}{5}\)

Bài 3: Tìm ba số x, y, z biết rằng \(\frac{x}{4} = \frac{y}{3} = \frac{z}{7}\) và 2x + y + 3z = 256

Bài 4: Cho hàm số \(y = - 3x\)

a, Vẽ đồ thị của hàm số

b, Trong các điểm A(4; 3); B (-6; 18); C (2; 6) và D(2; -6) điểm nào thuộc đồ thị của hàm số (có giải thích)

Bài 5: Cho tam giác ABC không cân, điểm I nằm ngoài tam giác ABC và thuộc nửa mặt phẳng có bờ là đường thẳng AC không chứa điểm B. Trên các tia đối của các tia IA, IB, IC theo thứ tự lấy điểm D, E, F sao cho ID = IA, IE = IB và IF = IC. Nối D với E, E với F và F với D.

a, Chứng minh \(\Delta ABC = \Delta DEF\)

b, Gọi M là điểm bất kỳ thuộc đoạn thẳng BC. Trên tia đối của tia IM lấy điểm M sao cho IN = IM. Chứng minh ba điểm E, F, N thẳng hàng

Bài 6: Cho biết xyz = 1. Tính giá trị \(A = \frac{x}{{xy + x + 1}} + \frac{y}{{yz + y + 1}} + \frac{z}{{xz + z + 1}}\)

B. Đáp án Đề ôn tập hè lớp 7 lên lớp 8 môn Toán

Bài 1:

a, \(\frac{{ - 23}}{3}\)

b, -1

c, 0

d, \(\frac{{ - 13}}{{16}}\)

Bài 2:

a, \(x \in \left\{ {3;8} \right\}\)

b, \(x = \frac{{17}}{7}\)

c, \(x = - 3\)

d, \(x = \frac{{ - 16}}{7}\)

Bài 3:

Có \(\frac{x}{4} = \frac{{2x}}{8};\frac{z}{7} = \frac{{3z}}{{21}}\) nên ta có \(\frac{{2x}}{8} = \frac{y}{3} = \frac{{3z}}{{21}} = \frac{{2x + y + 3z}}{{8 + 3 + 21}} = \frac{{256}}{{32}} = 8\)

Có \(\frac{x}{4} = 8 \Rightarrow x = 32;\frac{y}{3} = 8 \Rightarrow y = 24;\frac{z}{7} = 8 \Rightarrow z = 56\)

Bài 4:

a, Học sinh tự vẽ đồ thị hàm số

b,

Thay tọa độ điểm A vào hàm số có: \(3 = \left( { - 3} \right).4 \Leftrightarrow 3 = - 12\)(vô lý). Điểm A không thuộc đồ thị hàm số

Thay tọa độ điểm B vào hàm số có: \(18 = \left( { - 3} \right).\left( { - 6} \right) \Leftrightarrow 18 = 18\)(đúng). Điểm B thuộc đồ thị hàm số

Thay tọa độ điểm C vào đồ thị hàm số có: \(6 = \left( { - 3} \right).2 \Leftrightarrow 6 = - 6\)(vô lý). Điểm C không thuộc đồ thị hàm số

Thay tọa độ điểm D vào đồ thị hàm số có: \(6 = \left( { - 3} \right).\left( { - 2} \right) \Leftrightarrow 6 = 6\)(đúng). Điểm D thuộc đồ thị hàm số

Bài 5:

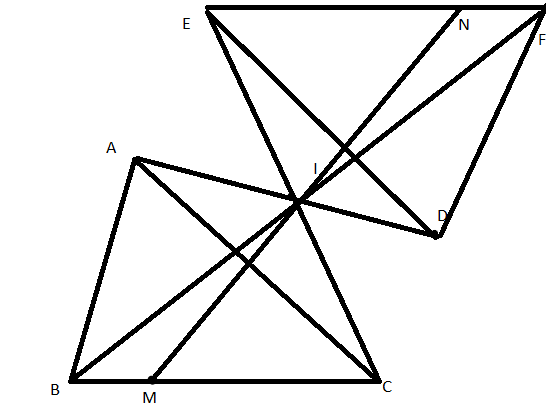
a, + Xét tam giác IAC và tam giác IDE có:

IA = ID (giả thiết)

\(\widehat {AIC} = \widehat {DIE}\)(hai góc đối đỉnh)

IE = IC (giả thiết)

Suy ra \(\Delta IAC = \Delta IDE\)(cạnh – góc – cạnh)

\(\Rightarrow AC = ED\)(cạnh tương ứng bằng nhau)

Chứng minh tương tự \(\Delta IAB = \Delta IDF \Rightarrow AB = DF\)

Và \(\Delta IBC = \Delta IFE \Rightarrow BC = EF\)

+ Xét tam giác ABC và tam giác DEF có:

AC = ED (cmt)

AB = DF (cmt)

BC = EF (cmt)

Suy ra \(\Delta ABC = \Delta DEF\)(cạnh – cạnh – cạnh)

b, + Có \(\Delta IBC = \Delta IFE\)(câu a) nên \(\widehat {IBC} = \widehat {IFE}\) (góc tương ứng bằng nhau)

mà hai góc ở vị trí so le trong

Suy ra BC // EF (1)

+ Xét tam giác IBM và tam giác IFN có:

IB = IF (giả thiết)

\(\widehat {BIM} = \widehat {FIN}\)(hai góc đối đỉnh)

IM = IN (giả thiết)

Suy ra \(\Delta IBM = \Delta IFN\)nên \(\widehat {IMB} = \widehat {INF}\)(góc tương ứng bằng nhau)

Mà hai góc ở ị trí so le trong

Suy ra BM // NF mà M thuộc BC nên BC // NF (2)

Từ (1) và (2) suy ra E, N, F thẳng hàng

Bài 6:

Có \(A = \frac{x}{{xy + x + 1}} + \frac{y}{{yz + y + 1}} + \frac{z}{{xz + z + 1}}\)

\(= \frac{{xz}}{{xyz + xz + z}} + \frac{{xyz}}{{xy{z^2} + xyz + xz}} + \frac{z}{{xz + z + 1}}\)

\(= \frac{{xz}}{{1 + xz + z}} + \frac{1}{{z + 1 + xz}} + \frac{z}{{xz + z + 1}} = \frac{{xz + z + 1}}{{xz + z + 1}} = 1\)

---------------------

Ngoài Bộ đề ôn tập hè lớp 7 lên lớp 8 trên, các em học sinh lớp 7 còn có thể tham khảo đề thi học kì 1 lớp 7 hay đề thi học kì 2 lớp 7 hoặc các tài liệu học tập lớp 8 mà VnDoc.com đã sưu tầm và chọn lọc để có thể chuẩn bị tốt nhất kiến thức trước khi vào năm học mới. Hy vọng với những tài liệu này, các em học sinh sẽ học tốt môn Toán lớp 7 hơn.