Bài tập Bất đẳng thức tam giác
Bài tập Toán lớp 7: Quan hệ giữa ba cạnh của một tam giác tập trung vào việc hướng dẫn phương pháp kiểm tra điều kiện tồn tại của một tam giác và cách vận dụng bất đẳng thức tam giác để giải các bài toán chứng minh, so sánh độ dài các cạnh một cách logic.
Với hệ thống bài tập được phân loại từ cơ bản đến nâng cao, đây là trợ thủ đắc lực giúp các em củng cố tư duy lập luận và rèn luyện kỹ năng giải toán chính xác. Tài liệu không chỉ hỗ trợ các em học tốt chương trình trên lớp mà còn là nguồn tham khảo giá trị để quý thầy cô làm phong phú thêm bài giảng của mình.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
Bài tập Toán 7: Bất đẳng thức tam giác
A. Một số kiến thức cần nhớ về bất đẳng thức tam giác
I. Phát biểu
+ Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại
+ Ta có tam giác ABC với ba cạnh lần lượt là AB, BC, AC thì:
AB + AC > BC
AB + BC > AC
AC + BC > AB
II. Chứng minh bất đẳng thức tam giác
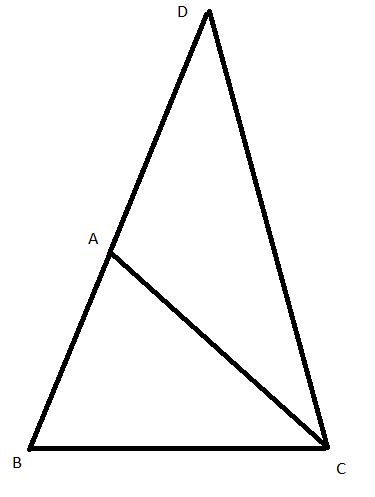
+ Trên tia đối của tia AB, lấy điểm D sao cho AD = AC
+ Do AB và AD là hai tia đối nhau nên điểm A nằm giữa hai điểm B và D. Suy ra tia CA nằm giữa hai tia CB và CD nên ta có: CB < CA < CD (1)
+ AD = AC nên tam giác ACD cân tại A. Suy ra CA = DA (2)
Từ (1) và (2) suy ra CB < DA < CD (3)
+ Trong tam giác BCD, từ (3) suy ra: AB + AC = BD > BC (điều phải chứng minh)
III. Hệ quả của bất đẳng thức tam giác
+ Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại
+ Tam giác ABC, có AB, BC, CA là độ dài các cạnh của tam giác ta có:
![]()
+ Chứng minh:
Ta có: AB + AC > BC (định lý của bất đẳng thức tam giác)
Suy ra AB > BC – AC
Tương tự, ta có:
AC > AB – BC; BC > AB – AC; AB > AC – BC; AC > BC – AB; BC > AC - AB
B. Bài tập vận dụng về bất đẳng thức tam giác
I. Bài tập trắc nghiệm
Câu 1: Ứng dụng bất đẳng thức tam giác, kiểm tra bộ ba đoạn thẳng nào dưới đây là ba cạnh của một tam giác:
| A. 15cm, 5cm, 20cm | B. 6cm, 4cm, 10cm |
| C. 9cm, 12cm, 15cm | D. 7cm, 13cm, 20cm |
Câu 2: Cho tam giác ABC có cạnh AB = 2cm và cạnh BC = 7cm. Tính độ dài cạnh AC biết độ dài cạnh AC là một số nguyên tố:
| A. 6cm | B. 5cm | C. 4cm | D. 3cm |
Câu 3: Cho tam giác ABC cân tại A có một cạnh bằng 7cm. Tính cạnh BC của tam giác đó biết chu vi của tam giác là 24cm:
| A. 9cm | B. 10cm | C. 12cm | D. 13cm |
Câu 4: Số tam giác có độ dài hai cạnh là 10cm và 4cm, độ dài cạnh thứ ba là một số nguyên là:
| A. 4 tam giác | B. 5 tam giác | C. 6 tam giác | D. 7 tam giác |
Câu 5: Cho tam giác ABC có điểm M là một điểm bất kì trong tam giác. Dấu “<, >, =” thích hợp để điền vào chỗ chấm: MB + MC … AB + AC là:
| A. < | B. = | C. > |
II. Bài tập tự luận
Bài 1: Cho tam giác ABC, điểm K là một điểm nằm trong tam giác. Gọi I là giao điểm của cạnh BK và AC
a, So sánh KA và KI + IA từ đó chứng minh KA + KB < IB + IA
b, So sánh IB với IC + CB từ đó chứng minh IB + IA < CA + CB
c, Chứng minh bất đẳng thức KA + KB < CA + CB
Bài 2: Cho tam giác ABC, biết AB = 3cm, AC = 6cm. Tính độ dài cạnh BC, biết độ dài này là một số nguyên tố. Khi đó tam giác ABC là tam giác gì?
C. Đáp án, lời giải bài tập về bất đẳng thức tam giác
I. Phần trắc nghiệm
| Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 |
| C | A | B | D | A |
I. Phần tự luận
Bài 1:
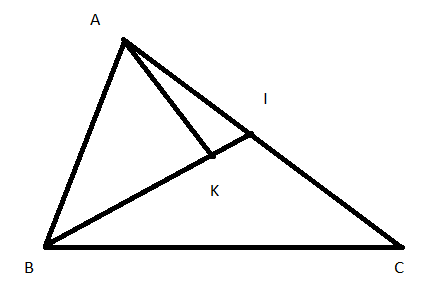
a, Xét tam giác AKI có theo bất đẳng thức tam giác ta được KA < KI + IA (1)
Cộng KB vào 2 vế bất đẳng thức (1) ta được:
AK + KB < KI + IA + KB
Nên AK + KB < IB + IA (3)
b, Xét tam giác ICB có theo bất đẳng thức tam giác ta được IB < IC + CB (2)
Cộng IA vào 2 vế bất đẳng thức (2) ta được:
IB + IA < IC + CB + IA
Hay IB + IA < (IC + IA) + CB
Nên IB + IA < AC + CB (4)
c, Từ (3) và (4) suy ra AM + MB < CA + CB
Bài 2:
Theo bất đẳng thức tam giác ABC ta có:
AC – AB < BC < AB + AC
Mà AB = 3cm và AC = 6cm suy ra 3 < BC < 11
Vì độ dài BC là một số nguyên tố nên BC = 5cm hoặc BC = 7cm
+ Với BC = 5cm, tam giác ABC là tam giác thường
+ Với BC = 7cm, tam giác ABC là tam giác thường
---------------
Trên đây VnDoc đã giới thiệu tới các bạn Bài tập Toán 7: Tam giác cân. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








