Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm, tính BC?

Giải Toán 7 Hình học chương 2

Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm, tính BC? là một dạng bài tập điển hình của định lý Pitago trong chương trình Toán lớp 7. Tài liệu này được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Bản quyền thuộc về VnDoc
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại

I. Kiến thức cần nhớ về định lý Pitago

1. Định lí Pitago

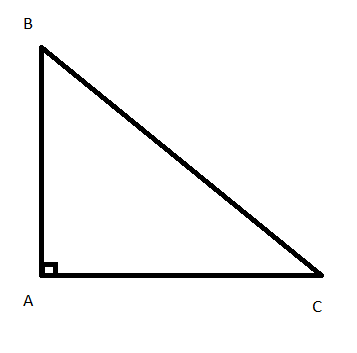
Bài tập Toán lớp 7: Định lý Pitago

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông

Tam giác ABC vuông tại A thì ta có: $B{C^2} = A{B^2} + A{C^2}$ $B{C^2} = A{B^2} + A{C^2}$

2. Định lí Pitago đảo

Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

Tam giác ABC có $B{C^2} = A{B^2} + A{C^2}$ $B{C^2} = A{B^2} + A{C^2}$ thì $\widehat {BAC} = {90^0}$ $\widehat {BAC} = {90^0}$ hay tam giác ABC vuông tại A

II. Bài tập ví dụ về định lý Pitago

Bài 1: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính BC.

Lời giải:

Xét tam giác ABC vuông tại A, áp dụng định lý Pitago có:

$A{B^2} + A{C^2} = B{C^2}$ $A{B^2} + A{C^2} = B{C^2}$

Thay số: ${6^2} + {8^2} = B{C^2} \Rightarrow B{C^2} = 100 \Leftrightarrow BC = 10$ ${6^2} + {8^2} = B{C^2} \Rightarrow B{C^2} = 100 \Leftrightarrow BC = 10$(cm)

Bài 2: Cho tam giác ABC vuông tại A, biết AB = 12cm, BC = 20cm

a, Tính AC

b, Lấy D thuộc AC sao cho DC = 7cm. Tính BD

Lời giải:

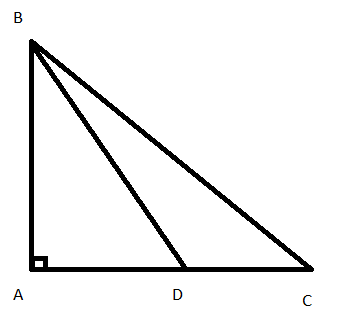
Bài tập Toán lớp 7: Định lý Pitago

a, Xét tam giác ABC vuông tại A, áp dụng định lý Pitago có:

$A{B^2} + A{C^2} = B{C^2}$ $A{B^2} + A{C^2} = B{C^2}$

Thay số: ${12^2} + A{C^2} = {20^2} \Leftrightarrow A{C^2} = 256 = {16^2} \Leftrightarrow AC = 16$ ${12^2} + A{C^2} = {20^2} \Leftrightarrow A{C^2} = 256 = {16^2} \Leftrightarrow AC = 16$(cm)

b, + Có AD + DC = AC. Suy ra AD = 16 – 7 = 9 (cm)

+ Xét tam giác ADC vuông tại A, áp dụng định lý Pitago có:

$A{D^2} + A{B^2} = B{D^2}$ $A{D^2} + A{B^2} = B{D^2}$

Thay số: ${9^2} + {12^2} = B{D^2} \Leftrightarrow B{D^2} = 225 \Leftrightarrow BD = 15$ ${9^2} + {12^2} = B{D^2} \Leftrightarrow B{D^2} = 225 \Leftrightarrow BD = 15$(cm)

Bài 3: Cho tam giác ABC có AB = 21cm, AC = 28cm, BC = 35cm. Chứng minh tam giác ABC là tam giác vuông

Lời giải:

Có $A{B^2} + A{C^2} = {21^2} + {28^2} = 1225$ $A{B^2} + A{C^2} = {21^2} + {28^2} = 1225$

$B{C^2} = {35^2} = 1225$ $B{C^2} = {35^2} = 1225$

Suy ra $A{B^2} + A{C^2} = B{C^2}$ $A{B^2} + A{C^2} = B{C^2}$. Theo định lý Pitago đảo suy ra tam giác ABC vuông tại A

III. Bài tập vận dụng về định lý Pitago

Bài 1: Cho tam giác ABC vuông tại A, biết AB = 15cm, AC = 20cm

a, Tính BC

b, Gọi D là trung điểm của AC, tính BD

Bài 2: Cho tam giác ABC cố AB = 15cm, BC = 20cm và AC = 25cm. Chứng minh AB vuông góc với BC

Bài 3: Cho tam giác ABC cân tại A, BC = 16cm, AB = 17cm. Gọi M là trung điểm của BC. Tính AM

Bài 4: Tìm độ dài của x trên hình vẽ:

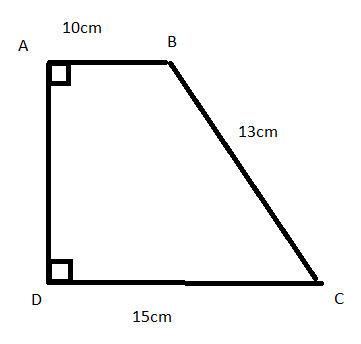
Bài tập Toán lớp 7: Định lý Pitago

Bài 5: Tìm số tự nhiên x sao cho x cùng với các số 24 và 25 lập thành độ dài của ba cạnh tam giác vuông

---------------

Trên đây VnDoc đã giới thiệu tới các bạn Bài tập Toán 7: Định lí Pi-ta-go. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc

Chia sẻ, đánh giá bài viết

7

6.742

Bài trước

Bài sau