Bài tập Toán lớp 7: Tổng ba góc của một tam giác

Bài tập Toán lớp 7: Tổng ba góc của một tam giác khái quát lý thuyết kèm bài tập vận dụng về Tổng 3 góc của một tam giác, giúp các em ôn tập các bài tập Toán lớp 7 chương 1 Hình học. Đây là tài liệu hữu ích giúp các em luyện tập các dạng Toán lớp 7 đạt kết quả tốt nhất, góp phần củng cố thêm kiến thức được học trong chương trình Toán 7.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. Lí thuyết Tổng 3 góc của một tam giác

- Định lí: Tổng ba góc của một tam giác bằng _{\({{180}^{0}}\)}

- Định lí: Trong tam giác vuông, hai góc nhọn phụ nhau.

- Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác ấy

- Tính chất: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

B. Bài tập Tổng ba góc của một tam giác

I. Bài tập trắc nghiệm

Câu 1: Cho tam giác ABC có _{\(\widehat{A}={{30}^{0}},\widehat{B}={{35}^{0}}\)}. Số đo _{\(\widehat{C}\)} là bao nhiêu?

\(A. \widehat{C}={{125}^{0}}\)	\(B. \widehat{C}={{115}^{0}}\)
\(C. \widehat{C}={{25}^{0}}\)	\(D. \widehat{C}={{95}^{0}}\)

Câu 2: Cho tam giác ABC có ba góc bằng nhau. Hỏi mỗi góc có số đo bằng bao nhiêu?

\(A. {{30}^{0}}\)	\(B. {{45}^{0}}\)
\(C. {{60}^{0}}\)	\(D. {{75}^{0}}\)

Câu 3: Cho tia phân giác ABC, kẻ phân giác BM, CN cắt nhau tại K. Biết góc A có số đo là _{\({{30}^{0}}\)}. Hỏi số đo góc _{\(\widehat{BKC}\)} bằng bao nhiêu?

		\(A. {{75}^{0}}\)	\(B. {{130}^{0}}\)
		\(C. {{105}^{0}}\)	\(D. {{87}^{0}}\)

Câu 4: Cho tam giác ABC, góc _{\(\widehat{ACx}={{125}^{0}}\)} là góc ngoài đỉnh C. Khẳng định nào sau đây đúng?

\(A. \widehat{A}+\widehat{B}<{{125}^{0}}\)	\(C. \widehat{A}+\widehat{B}>{{125}^{0}}\)
\(B. \widehat{A}+\widehat{B}={{125}^{0}}\)	\(D. \widehat{A}+\widehat{B}\ne {{125}^{0}}\)

II. Bài tập tự luận

Câu 1: Cho tam giác ABC có _{\(\widehat{A}<{{90}^{0}}\)}, từ B vẻ BD vuông góc với AC, từ C kẻ CE vuông góc với AB, BD cắt CE tại K. Tính số đo góc _{\(\widehat{EKD}\)}, biết _{\(\widehat{ACB}={{30}^{0}},\widehat{ABC}={{70}^{0}}\)}

Câu 2: Cho tam giác ABC biết góc _{\(\widehat{A}={{30}^{0}}\)}. Kẻ tia phân giác BD và CE của hai góc B và C. Biết rằng _{\(\widehat{AEC}=\widehat{ADB}\)}. Tính số đo các góc _{\(\widehat{C},\widehat{B}\)} của tam giác ABC.

Câu 3: Cho tam giác ABC có _{\(\widehat{B}={{65}^{0}},\widehat{C}={{65}^{0}}\)}. Vẽ tia Am song song với BC, tia An là tia đối của tia AB và tia Am nằm giữa hai tia An, AC

a. Tính số đo góc _{\(\widehat{BAC}\)}

B. Tính số đo góc _{\(\widehat{BAm}\)}

c. Chứng minh Am là tia phân giác của góc _{\(\widehat{nAC}\)}

III. Lời giải bài tập Tổng ba góc của một tam giác

Đáp án bài tập trắc nghiệm

1. B

2.C

3.C

4.B

Đáp án bài tập tự luận

Câu 1:

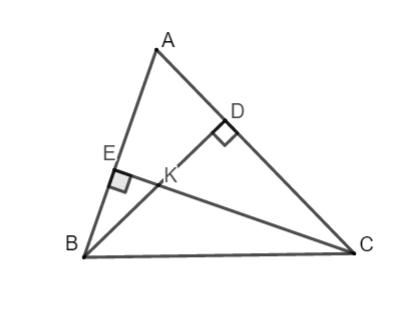
Xét tam giác BCD vuông tại D ta có:

\(\begin{align} & \widehat{DBC}+\widehat{DCB}={{90}^{0}}\Rightarrow \widehat{DBC}={{90}^{0}}-\widehat{DCB} \\ & \Rightarrow \widehat{DBC}=90-60={{30}^{0}} \\ \end{align}\)

Tương tự xét tam giác BEC vuông tại E có:

\(\begin{align} & \widehat{EBC}+\widehat{ECB}={{90}^{0}}\Rightarrow \widehat{ECB}={{90}^{0}}-\widehat{EBC} \\ & \Rightarrow \widehat{EBC}=90-70={{20}^{0}} \\ \end{align}\)

Xét tam giác KCB có:

Tổng ba góc của một tam giác bằng \({{180}^{0}}\) nên ta có:

\(\begin{align} & \widehat{KBC}+\widehat{KCB}+\widehat{BKC}={{180}^{0}}\Rightarrow \widehat{BKC}={{180}^{0}}-\left( {{20}^{0}}+{{30}^{0}} \right) \\ & \Rightarrow \widehat{BKC}={{130}^{0}} \\ \end{align}\)

Do \(\widehat{BKC}=\widehat{EKD}\) (đối đỉnh)

\(\Rightarrow \widehat{EKD}={{130}^{0}}\)

Câu 2:

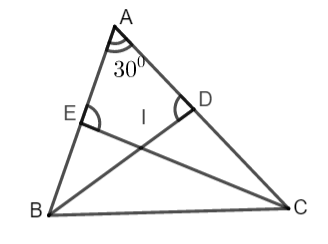
Xét tam giác ADB có:

_{\(\widehat{A}+\widehat{ABD}+\widehat{ADB}={{180}^{0}}\Rightarrow \widehat{ABD}={{180}^{0}}-\left( \widehat{ADB}+\widehat{A} \right)\)} (1)

(theo định lí tổng ba góc của tam giác)

Xét tam giác AEC có:

_{\(\widehat{A}+\widehat{AEC}+\widehat{ACE}={{180}^{0}}\Rightarrow \widehat{ACE}={{180}^{0}}-\left( \widehat{AEC}+\widehat{A} \right)\)}(2)

(theo định lí tổng ba góc của tam giác)

Do _{\(\widehat{AEC}=\widehat{ADB}\)} (3)

Từ (1), (2), (3) ta có _{\(\widehat{ABD}=\widehat{ACE}\)} (4)

Do BD và CE là phân giác góc B và C nên

_{\(\widehat{ABD}=\frac{1}{2}\widehat{B},\widehat{ACE}=\frac{1}{2}\widehat{C}\)} (5)

Từ (4) và (5) ta có: _{\(\widehat{B}=\widehat{C}\)}

Xét tam giác ABC có

\(\begin{align} & \widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}} \\ & \Rightarrow \widehat{B}+\widehat{C}={{180}^{0}}-\widehat{A}={{180}^{0}}-{{30}^{0}}={{150}^{0}} \\ & \Rightarrow \widehat{B}=\widehat{C}=\frac{{{150}^{0}}}{2}={{75}^{0}} \\ \end{align}\)

Câu 3:

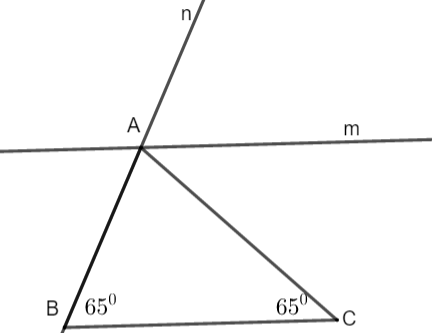
a. Xét tam giác ABC có:

\(\begin{align} & \widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}} \\ & \Rightarrow \widehat{A}={{180}^{0}}-\left( \widehat{B}+\widehat{C} \right)={{180}^{0}}-\left( {{65}^{0}}+{{65}^{0}} \right)={{50}^{0}} \\ \end{align}\)

b. Ta có: Am song song với BC nên \(\widehat{BCA}=\widehat{CAm}={{65}^{0}}\)(so le trong)

Mặt khác: _{\(\widehat{BAm}=\widehat{BCA}+\widehat{CAm}={{50}^{0}}+{{65}^{0}}={{115}^{0}}\)}

c. Ta có Am song song với BC nên _{\(\widehat{mAn}=\widehat{CBA}={{65}^{0}}\)}(đồng vị) (1)

Theo câu b: _{\(\widehat{BCA}=\widehat{CAm}={{65}^{0}}\)} (2)

Từ (1) và (2) suy ra _{\(\widehat{mAn}=\widehat{CAm}\)}

Vậy Am là tia phân giác của góc _{\(\widehat{nAC}\)}

-------------------------------------------------

Như vậy, VnDoc.com đã gửi tới các bạn Bài tập Toán lớp 7: Tổng ba góc của một tam giác. Hy vọng đây là tài liệu hữu ích giúp các em nắm vững các dạng toán về Tổng 3 góc của 1 tam giác, từ đó vận dụng vào làm các bài tập liên quan hiệu quả.

Ngoài ra, các em học sinh có thể tham khảo thêm các tài liệu khác do VnDoc sưu tầm và chọn lọc như Giải Toán 7, Giải SBT Toán 7, Chuyên đề Toán 7,... để học tốt môn Toán hơn và chuẩn bị cho các bài thi đạt kết quả cao.