Bài tập Toán lớp 7: Hai góc đối đỉnh
Bài tập Hai góc đối đỉnh
Bài tập Toán lớp 7: Hai góc đối đỉnh là tài liệu ôn tập với các bài tập Toán lớp 7 chương 1, giúp các em học sinh luyện tập các dạng Toán lớp 7 đạt kết quả tốt nhất, góp phần củng cố thêm kiến thức của các em.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
A. Lý thuyết Hai góc đối đỉnh
1. Định nghĩa
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia
2. Tính chất
+ Hai góc đối đỉnh thì bằng nhau
B. Bài tập Hai góc đối đỉnh
I. Bài tập trắc nghiệm
Câu 1: Cho hai đường thẳng aa’ và bb’ cắt nhau tại O. Góc đối đỉnh với góc 
\(\widehat {a'Ob}\) là:
| A. \(\widehat {a'Ob}\) |
B. \(\widehat {aOb}\) |
C. \(\widehat {a'Ob'}\) |
D. \(\widehat {aOb'}\) |
Câu 2: Chọn phát biểu đúng trong các phát biểu dưới đây:
A. Hai góc bằng nhau là hai góc đối đỉnh
B. Tổng của hai góc đối đỉnh bằng 1800
C. Hai đường thẳng cát nhau tạo thành hai cặp góc đối đỉnh
D. Hai góc bằng nhau và có chung đỉnh là hai góc đối đỉnh
Câu 3: Cho hai đường thẳng xy và zt cắt nhau tại A. Góc đối đỉnh với góc \(\widehat {xAt}\) là:
| A. \(\widehat {yAz}\) |
B. \(\widehat {yAt}\) |
C. \(\widehat {zAt}\) |
D. \(\widehat {xAy}\) |
Câu 4: Cho hai đường thẳng ab và cd cắt nhau tại O. Biết góc \(\widehat {aOc} = {72^0}\). Số đo của góc là:
| A. 970 | B. 500 | C. 720 | D. 1080 |
Câu 5: Cho ba đường thẳng ab, cd và mn cắt nhau tại O. Số cặp góc đối đỉnh được tạo thành là:
| A. 5 cặp | B. 6 cặp | C. 7 cặp | D. 8 cặp |
II. Bài tập tự luận
Bài 1: Vẽ bốn đường thẳng xx’, yy’, zz’ và tt’ cùng đi qua điểm O. Hãy viết tên các cặp góc đối đỉnh (khác góc bẹt)
Bài 2: Cho góc \(\widehat {xOy}\) có số đo bằng 500. Vẽ hai tia Om và On lần lượt là tia đối của tia Oy và Ox. Tính số đo các góc còn lại trên hình
Bài 3: Vẽ \(\widehat {x'Ay'}\) đối đỉnh với \(\widehat {xAy}\). Vẽ tia phân giác Az của \(\widehat {xAy}\) và tia đối At của tia Az. So sánh \(\widehat {x'At}\) và \(\widehat {y'At}\)
Bài 4: Hai đường thẳng AB và CD cắt nhau tại O sao cho \(\widehat {AOC} = {60^0}\).
a, Tính số đo các góc còn lại
b, Vẽ tia Ot là phân giác của \(\widehat {AOC}\) và Ot’ là tia đối của tia Ot. Chứng minh Ot' là tia phân giác của \(\widehat {BOD}\)
C. Lời giải bài tập Hai góc đối đỉnh
I. Bài tập trắc nghiệm
| Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 |
| D | C | A | C | B |
II. Bài tập tự luận
Bài 1:
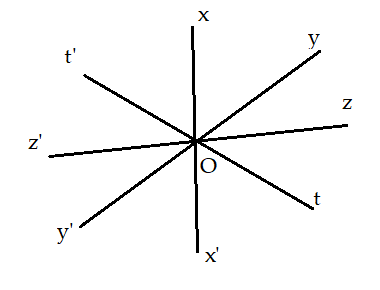
Các cặp góc đối đỉnh (khác góc bét là): \(\widehat {xOy}\) và \(\widehat {x'Oy'}\); \(\widehat {yOz}\) và \(\widehat {y'Oz'}\); \(\widehat {zOt}\) và \(\widehat {z'Ot'}\); \(\widehat {tOx'}\)và \(\widehat {t'Ox}\); \(\widehat {xOz}\) và \(\widehat {x'Oz'}\); \(\widehat {yOt}\) và \(\widehat {y'Ot'}\); \(\widehat {zOx'}\) và \(\widehat {z'Ox}\); \(\widehat {tOy'}\)và \(\widehat {t'Oy}\); \(\widehat {xOt}\) và \(\widehat {x'Ot'}\); \(\widehat {yOx'}\)và \(\widehat {y'Ox}\); \(\widehat {zOy}'\)và \(\widehat {z'Oy}\); \(\widehat {tOz'}\)và \(\widehat {t'Oz}\)
Bài 2:
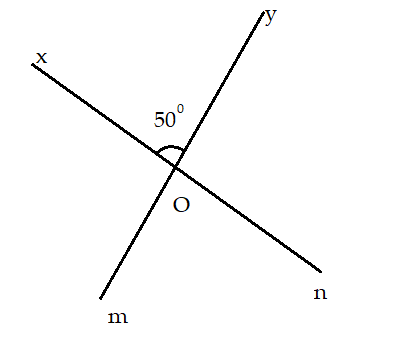
+ Có \(\widehat {xOy}\) và \(\widehat {mOn}\) là hai góc đối đỉnh nên \(\widehat {xOy} = \widehat {mOn} = {50^0}\)
+ Có Ox và On là hai tia đối nhau nên \(\widehat {xOy}\) và \(\widehat {yOn}\) là hai góc kề bù
\(\begin{array}{l}
\Rightarrow \widehat {xOy} + \widehat {yOn} = {180^0}\\
{50^0} + \widehat {yOn} = {180^0}\\
\Rightarrow \widehat {yOn} = {180^0} - {50^0} = {130^0}
\end{array}\)
+ Có \(\widehat {nOy}\) và \(\widehat {mOx}\) là hai góc đối đỉnh nên \(\widehat {nOy} = \widehat {mOz} = {130^0}\)
Bài 3:
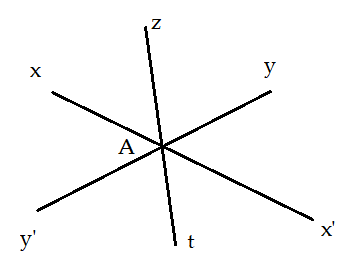
+ Có \(\widehat {x'Ay'}\) và \(\widehat {xAy}\) là góc đối đỉnh nên Ax và Ax’ là hai tia đối nhau, Ay và Ay’ là hai tia đối nhau
+ Có Az là tia phân giác của \(\widehat {xAy}\) nên \(\widehat {xAz} = \widehat {zAy}\)(1)
+ Az và At là hai tia đối nhau; Ax và Ax’ là hai tia đối nhau \(\widehat {xAz}\) nên đối đỉnh với \(\widehat {x'At}\). Suy ra \(\widehat {x'At} = \widehat {xAz}\)(2)
+ Az và At là hai tia đối nhau; Ay và Ay’ là hai tia đối nhau nên \(\widehat {yAz}\) đối đỉnh với \(\widehat {y'At}\). Suy ra \(\widehat {y'At} = \widehat {yAz}\)(3)
+ Từ (1), (2) và (3) suy ra \(\widehat {y'At} = \widehat {tAx'}\)
Bài 4:
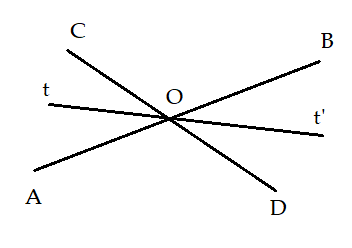
a, + Có \(\widehat {AOC}\) và \(\widehat {BOD}\) là hai góc đối đỉnh nên \(\widehat {AOC} = \widehat {BOD} = {60^0}\)
+ Có \(\widehat {AOC}\) và \(\widehat {BOC}\) là hai góc kề bù nên \(\widehat {AOC} + \widehat {BOC} = {180^0}\)
\(\begin{array}{l}
{60^0} + \widehat {BOC} = {180^0}\\
\Rightarrow \widehat {BOC} = {180^0} - {60^0} = {120^0}
\end{array}\)
+ Có \(\widehat {BOC}\) và \(\widehat {DOA}\) là hai góc đối đỉnh nên \(\widehat {BOC} = \widehat {DOC} = {120^0}\)
b, Vì Ot là tia phân giác của \(\widehat {AOC}\) nên \(\widehat {AOt} = \widehat {tOC} = \frac{{{{60}^0}}}{2} = {30^0}\)
Có \(\widehat {AOt}\) và \(\widehat {BOt'}\) là hai góc đối đỉnh nên \(\widehat {AOt} = \widehat {BOt'} = {30^0}\)
Có \(\widehat {COt}\) và \(\widehat {DOt'}\) là hai góc đối đỉnh nên \(\widehat {COt} = \widehat {DOt'} = {30^0}\)
Suy ra có \(\widehat {BOt'} = \widehat {DOt'} = \frac{{\widehat {BOD}}}{2}\) nên Ot’ là tia phân giác của \(\widehat {BOD}\)
-------
Như vậy, VnDoc.com đã gửi tới các bạn Bài tập Toán lớp 7: Hai góc đối đỉnh. Ngoài ra, các em học sinh có thể tham khảo thêm các tài liệu khác do VnDoc sưu tầm và chọn lọc như Giải Toán 7, Giải SBT Toán 7, Chuyên đề Toán 7,... để học tốt môn Toán hơn và chuẩn bị cho các bài thi đạt kết quả cao.
