Công thức tính diện tích tam giác: vuông, thường, cân, đều

Công thức tính diện tích tam giác: vuông, thường, cân, đều

Có rất nhiều các cách khác nhau để tính diện tích tam giác với nhiều công thức được sử dụng phổ biến cũng như công thức khi sử dụng cần được phải chứng minh. Ở bài viết này, VnDoc sẽ giới thiệu đến các bạn những cách tính diện tích tam giác dễ hiểu và được sử dụng nhiều nhất để bạn có thể áp dụng ngay trong các bài thi.

• Đề ôn tập ở nhà môn Toán lớp 8 - Nghỉ dịch nCoV
• Bài ôn tập ở nhà nghỉ phòng chống dịch bệnh môn Hóa lớp 8
• Bài ôn tập ở nhà nghỉ phòng chống dịch bệnh môn Vật lý lớp 8
• Bài tập ôn tập ở nhà trong thời gian nghỉ phòng chống dịch bệnh - Môn Ngữ văn 8
• Đề ôn tập ở nhà môn Ngữ văn lớp 8 - Nghỉ dịch nCoV

Để tính diện tích tam giác bạn cần xác định loại tam giác đó là gì, từ đó tìm ra công thức tính diện tích chính xác và các yếu tố cần thiết để tính diện tích tam giác nhanh nhất.

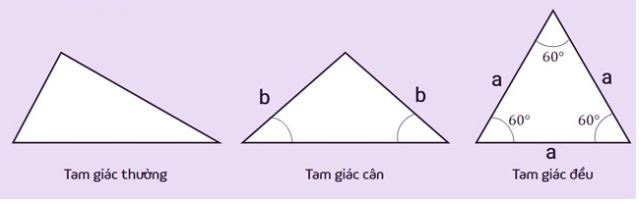
Các loại tam giác

Tam giác thường: là tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau. Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt của tam giác.

Tam giác cân: là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy. Tính chất của tam giác cân là hai góc ở đáy thì bằng nhau.

Tam giác đều: là trường hợp đặc biệt của tam giác cân có cả ba cạnh bằng nhau. Tính chất của tam giác đều là có 3 góc bằng nhau và bằng \(60^o\).

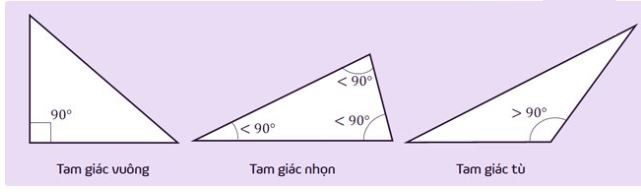
Tam giác vuông: là tam giác có một góc bằng \(90^o\) (là góc vuông).

Tam giác tù: là tam giác có một góc trong lớn hơn lớn hơn \(90^o\)(một góc tù) hay có một góc ngoài bé hơn \(90^o\) (một góc nhọn).

Tam giác nhọn: là tam giác có ba góc trong đều nhỏ hơn \(90^o\) (ba góc nhọn) hay có tất cả góc ngoài lớn hơn \(90^o\) (sáu góc tù).

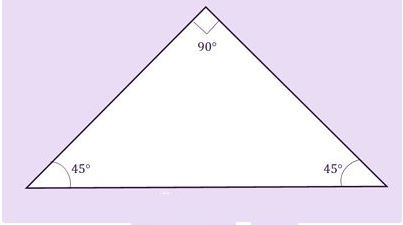
Tam giác vuông cân: vừa là tam giác vuông, vừa là tam giác cân.

Công thức diện tích tam giác

1. Tính diện tích tam giác thường

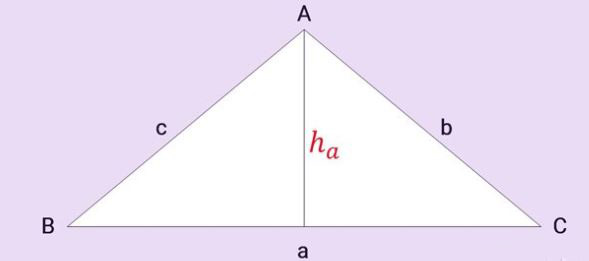
Tam giác ABC có ba cạnh a, b, c, h_a là đường cao từ đỉnh A như hình vẽ:

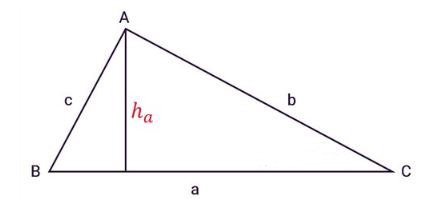
a. Công thức chung

Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.

\(S_{A B C}=\frac{1}{2} a \cdot h_{a}=\frac{1}{2} b \cdot h_{b}=\frac{1}{2} c \cdot h_{c}\)

b. Tính diện tích tam giác khi biết một góc

Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.

\(S_{A B C}=\frac{1}{2} a . b . \sin \hat{C}=\frac{1}{2} a . c . \sin \hat{B}=\frac{1}{2} b . c . \sin \hat{A}\)

c. Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron.

Sử dụng công thức Heron đã được chứng minh:

\(S=\sqrt{p(p-a)(p-b)(p-c)}\)

Với p là nửa chu vi tam giác:

\(p=\frac{1}{2}(a+b+c)\)

Có thể viết lại bằng công thức:

\(S=\frac{1}{4} \sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)}\)

d. Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R).

\(S_{A B C}=\frac{a b c}{4 R}\)

Cách khác: \(S_{A B C}=2 \cdot R^{2} \cdot \sin \hat{A} \cdot \sin \hat{B} \cdot \sin \hat{C}\)

Lưu ý: Cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.

e. Tính diện tích bằng bán kính đường tròn nội tiếp tam giác (r).

\(S_{A B C}=p \cdot r\)

2. Tính diện tích tam giác cân

Tam giác cân ABC có ba cạnh, a là độ dài cạnh đáy, b là độ dài hai cạnh bên, h_a là đường cao từ đỉnh A như hình vẽ:

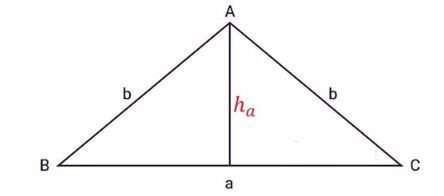
Áp dụng công thức tính diện tích thường, ta có công thức tính diện tích tam giác cân:

\(S_{A B C}=\frac{1}{2} a \cdot h_{a}\)

3. Tính diện tích tam giác đều

Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài các cạnh như hình vẽ:

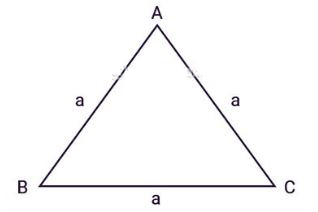
Áp dụng định lý Heron để suy ra, ta có công thức tính diện tích tam giác đều:

\(S_{A B C}=a^{2} \frac{\sqrt{3}}{4}\)

4. Tính diện tích tam giác vuông

Tam giác ABC vuông tại B, a, b là độ dài hai cạnh góc vuông:

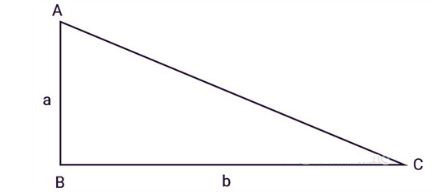
Áp dụng công thức tính diện tích thường cho diện tích tam giác vuông với chiều cao là 1 trong 2 cạnh góc vuông và cạnh đáy là cạnh còn lại.

Công thức tính diện tích tam giác vuông:

\(S_{A B C}=\frac{1}{2} a . b\)

5. Tính diện tích tam giác vuông cân

Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông:

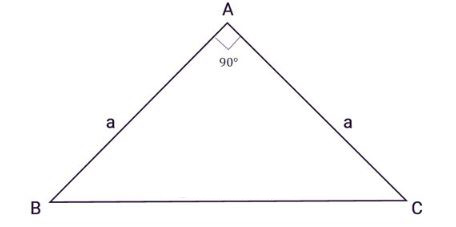
Áp dụng công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, ta có công thức:

\(S_{A B C}=\frac{1}{2} a^{2}\)