Đề thi kiểm định chất lượng môn Toán lớp 9 huyện Hiệp Hòa, Bắc Giang năm 2016 (Lần 3)
Đề thi kiểm tra chất lượng môn Toán lớp 9
Đề thi kiểm định chất lượng môn Toán lớp 9 huyện Hiệp Hòa, Bắc Giang năm 2016 (Lần 3) có 5 câu hỏi cùng đáp án đi kèm. Đây là tài liệu ôn tập hữu ích dành cho các bạn học sinh lớp 9, giúp các bạn củng cố kiến thức và chuẩn bị tốt nhất cho kì thi tuyển sinh vào lớp 10, kì thi cuối năm hiệu quả.
77 đề thi vào lớp 10 môn Toán các trường chuyên
| PHÒNG GD&ĐT HIỆP HÒA |
ĐỀ THI KIỂM ĐỊNH CHẤT LƯỢNG TOÁN 9 LẦN 3 NĂM HỌC 2015 - 2016 MÔN THI: TOÁN Ngày thi: 18/01/2016 Thời gian làm bài: 120 phút (Không kể thời gian giao đề) |
Câu I (2,5 điểm)
Tính giá trị của biểu thức: P = √2(√8 - 2√3) + 2√6
Tìm x để căn thức sau có nghĩa: ![]()
3. Tìm a và b để đường thẳng (d): (a - 2)x + b có hệ số góc bằng 4 và đi qua điểm M(1;-3).
Câu II (2,5 điểm)
1. Cho biểu thức:
![]()
a. Rút gọn biểu thức B.
b. Tìm giá trị nhỏ nhất của biểu thức B.
2. Cho hệ phương trình:
![]()
Tìm a và b biết hệ phương trình đã cho có nghiệm (x; y) = (2; 3).
Câu III (1,5 điểm)
Một xe máy dự định đi quãng đường dài 60 km trong một thời gian nhất định. Trên thực tế, xe máy đi nửa quãng đường đầu với vận tốc lớn hơn vận tốc dự định là 10 km/h, và đi nửa quãng đường còn lại với vận tốc thấp hơn vận tốc dự định là 6 km/h nhưng xe máy đã đến đúng thời gian đã định. Tính thời gian xe máy dự định đi quãng đường trên.
Câu IV (3 điểm)
Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn sao cho MA < MB. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM.
a) Chứng minh bốn điểm E, M, N, C cùng nằm trên một đường tròn.
b) Chứng minh NE vuông góc với AB.
c) Vẽ điểm F đối xứng với E qua M. Chứng minh rằng tứ giác AENF là hình thoi.
d) Chứng minh FN là tiếp tuyến của đường tròn (B; BA).
Câu V (0,5 điểm)
Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
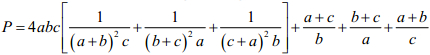
Đáp án đề kiểm tra chất lượng môn Toán lớp 9
Câu I
1 (1 điểm)
P = √2(√8 - 2√3) + 2√6 = √2.√8 - 2√2.√3 + 2√6 = √16 - 2√6 + 2√6
= 4
2 (0,75 điểm)
![]() có nghĩa ↔ 3x - 6 ≥ 0
có nghĩa ↔ 3x - 6 ≥ 0
3x ≥ 6 ↔ x ≥ 2
Vậy với x ≥ 2 thì A có nghĩa
3 (0,7 điểm)
Đường thẳng d có hệ số góc bằng 4 ↔ a - 2 = 4 ↔ a = 6
Mặt khác (d) đi qua điểm M (1;-3) nên thay a = 6, x = 1; y = -3 vào y = (a - 2)x + b.
Khi đó ta có: -3 = (6 - 2).1 + b
→ -3 = 4 + b
→ b = -7
Vậy a = 6 và b = -7 là các giá trị cần tìm và khi đó (d): y = 4x - 7
Câu II
1 (1,75đ)
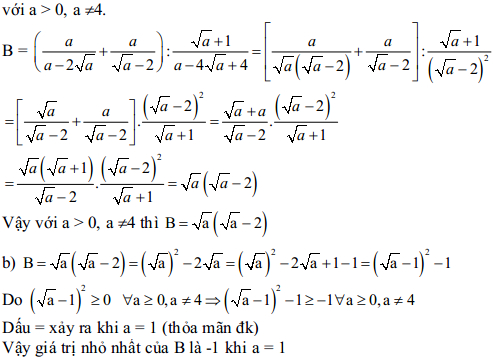
(Còn tiếp)