Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Văn Giang - Hưng Yên lần 1
Đề minh họa môn Toán năm 2019 có đáp án
SỞ GD&ĐT HƯNG YÊN
TRƯỜNG THPT VĂN GIANG
(Đề gồm: 06 trang)
KỲ THI THỬ THPT QUỐC GIA LẦN 1 NĂM 2019
Môn: TOÁN
Thời gian làm bài: 90 phút
Họ tên
:............................................................
Số báo danh
: ................ Phòng thi: …....
Câu 1: Diện tích hình phẳng được giới hạn bởi hai đường
2
y x 3x
và
y x
bằng (đvdt).
A. 2. B.
8
3
. C.
16
3
. D.
32
3
.
Câu 2: Cho hình chóp SABCD có SA vuông góc với đáy góc giữa SC và đáy là.
A.
SCA
. B.
SAC
. C.
SDA
. D.
SBA
.
Câu 3: Tập xác định D của hàm số
3
y 3x 5
là :
A.
5
\
3
.
B.
5
;
3
. C.
5
;
3
. D.
3
;
5
.
Câu 4: Giả sử
b b
a c
f (x)dx 2, f (x)dx 3
với
a b c
thì
c
a
f (x)dx
bằng?
A.
5
. B.
1
. C.
1
. D.
5
.
Câu 5: Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
0; 2; 1 , 2; 4;3 , 1;3; 1
A B C
và mặt phẳng
: 2 3 0.
P x y z
Tìm điểm
M P
sao cho
2
MA MB MC
đạt giá trị nhỏ
nhất.
A.
2;2; 4
M
. B.
2; 2;4
M
. C.
1 1
; ;1
2 2
M
. D.
1 1
; ; 1
2 2
M
.
Câu 6: Hàm số nào sau đây nghịch biến trên từng khoảng xác định?
A.
4 2
y x x
. B.
y 2x sin x
. C.
x 1
y
x 2
. D.
3 2
y x 3x
.
Câu 7: Số phức z thỏa mãn
z 2z 3 2i
là:
A.
1 2i
. B.
1 2i
. C.
2 i
. D.
2 i
.
Câu 8: Sau Tết Nguyên đán Kỉ Hợi, bé Nam được tổng tiền lì xì là 15 triệu động. Bố Nam gửi toàn
bộ số tiền trên của con vào ngân hàng với lãi suất ban đầu là 5%/năm, tiền lãi hàng năm được nhập
vào gốc và sau một năm thì lãi suất tăng 0,2% so với năm trước đó. Hỏi sau 5 năm tổng tiền của bé
Nam trong ngân hàng.
A. 19,5 triệu đồng. B. 19,6 triệu đồng. C. 13,5 triệu đồng. D. 14,5 triệu đồng.
Câu 9: Giải phương trình
2
2
2
log x 3.log x 2 0
. Ta có tổng các nghiệm là:
A.
5
2
. B. 6. C.
9
2
. D. 3.
Câu 10: Cho hàm số
2 1
1
x
y
x
. Phương trình tiếp tuyến tại điểm
2;5
M
của đồ thị hàm số trên là.
Mã đề 111
A.
3 11
y x
. B.
3 11
y x
. C.
3 11
y x
. D.
3 11
y x
.
Câu 11: Viết phương trình của mặt phẳng trung trực (P) của đoạn AB với
1, 4, 3 ; 3, 6, 5 .
A B
A.
5 11 0x y z
. B.
5 11 0x y z
.
C.
5 16 0x y z
. D.
5 11 0x y z
.
Câu 12: Cho hàm số
y f x
có đạo hàm
2
2
' 2 3
f x x x x
. Khi đó số điểm cực trị của hàm
số
y f x
là.
A. 3. B. 5. C. 2. D. 1.
Câu 13: Cho số phức z thỏa mãn điều kiện
3 z 3i 1 5.
Tập hợp các điểm biểu diễn của.
Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.
A.
S 16
. B.
S 4
. C.
S 25
. D.
S 8
.
Câu 14: Cho hàm số
y f x
có bảng biến thiên sau. Mệnh đề nào dưới đây sai?
.
A. Điểm cực đại của đồ thị hàm số
1;2
.
B. Hàm số không đạt cực tiểu tại điểm
2
x
.
C. Hàm số đạt cực đại tại điểm
1
x
.
D. Giá trị cực đại của hàm số là
2
y
.
Câu 15: Giá trị lớn nhất và nhỏ nhất của hàm số
3 2
2 3 1
y x x
trên đoạn
2;1
lần lượt là.
A. 4 và
5
. B. 7 và
10
. C. 1 và
2
. D. 0 và
1
.
Câu 16: Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số
2
1
y x
và trục Ox quanh trục Ox .
A.
5
3
. B.
16
15
. C.
4
. D.
3
.
Câu 17: Công thức nguyên hàm nào sau đây không đúng?
A.
dx
ln x C
x
. B.
1
x
x dx C 1
1
.
C.
x
x
a
a dx C 0 a 1
ln a
. D.
dx
tan x C
cos x
.
Câu 18: Cho hàm số
y f x
có đạo hàm liên tục trên
R
. Biết
1 1
f
và
2
1 3 2 .x f x f x x x
Tính giá trị
2
f
.
A.
5
2
2
f
.
B.
2 3
f
. C.
2 2
f
. D.
2
2
3
f
.
Câu 19: Cho một tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN
nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định
x
'y
y
1
0
2
2
0
1
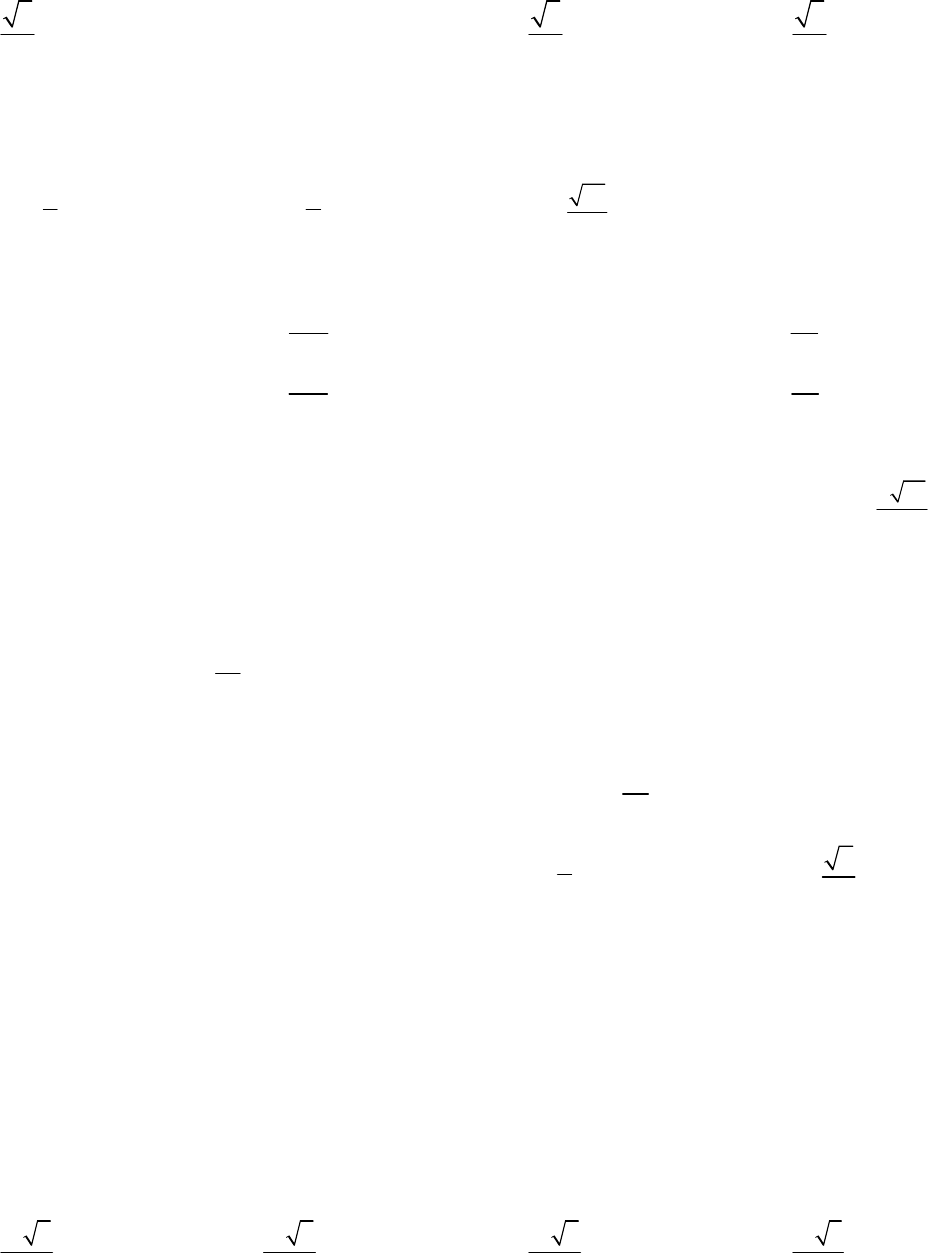
giá trị lớn nhất của diện tích hình chữ nhật đó?
A.
2
3
a
2
. B.
0
. C.
2
3
a
4
. D.
2
3
a
8
.
Câu 20: Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
: 2 2 4 0
P x y z
và điểm
1; 2;3
A
. Tính khoảng cách
d
từ
A
đến
( )P
.
A.
7
3
d
. B.
7
9
d
. C.
14
2
d
. D.
1
d
.
Câu 21: Phương trình mặt cầu tâm
I 3; 2;4
và tiếp xúc với
P : 2x y 2z 4 0
là:
A.
2 2 2
400
x 3 y 2 z 4
9
. B.
2 2 2
20
x 3 y 2 z 4
3
.
C.
2 2 2
400
x 3 y 2 z 4
9
. D.
2 2 2
20
x 3 y 2 z 4
3
.
Câu 22: Trong không gian với hệ trục tọa độ Oxyz, cho
(1; 0; 2), (3;1; 4), (3; 2;1)A B C
. Tìm tọa độ
điểm S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng
3 11
2
và S
có cao độ âm.
A.
4;6; 4
S
. B.
4; 6; 4
S
. C.
4;6; 4
S
. D.
4; 6; 4
S
.
Câu 23: Cho hàm số
4
2 2
2 2
2
x
y m x
. Tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ
thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành
qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng
64
15
là.
A.
1
. B.
. C.
1
; 1
2
. D.
2
; 1
2
.
Câu 24: Cho hàm số
y f x
liên tục, luôn dương trên
0;2
và thỏa mãn
2
0
5
I f x dx
. Khi đó
giá trị của tích phân
2
2 ln
0
3
f x
K e dx
là.
A.
2
5 6
e
. B.
2
5 6
e
. C.
2
6 5
e
. D.
2
5 9
e
.
Câu 25: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B với AC = a biết SA vuông
góc với đáy ABC và SB hợp với đáy một góc 60
o
. Tính thể tích hình chóp.
A.
3
a 6
24
. B.
3
a 6
8
. C.
3
a 6
48
.
D.
3
a 3
24
.
Câu 26: Cho một khối trụ có khoảng cách giữa hai đáy bằng 10, biết diện tích xung quanh của khối
trụ bằng
80
. Thể tích của khối trụ là:
A.
160
. B.
144
. C.
164
. D.
64
.
Câu 27: Một hình nón có đường cao
20h cm
, bán kính đáy
25r cm
. Tính diện tích xung quanh
Đề thi thử Toán THPT Quốc gia năm 2019
VnDoc xin giới thiệu tới bạn đọc Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Văn Giang - Hưng Yên lần 1. Nội dung tài liệu gồm 50 câu hỏi trắc nghiệm, thời gian làm bài 90 phút. Mời các bạn học sinh tham khảo.
- Đề thi thử THPT Quốc gia môn Toán năm 2019 Sở GD&ĐT Hà Nội
- Đề thi thử THPT Quốc gia môn Ngữ văn năm 2019 Sở GD&ĐT Hà Nội
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Lý Nhân Tông - Bắc Ninh lần 3
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Trần Phú - Hà Tĩnh lần 2
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Ngô Quyền - Hải Phòng lần 2
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Chuyên Lê Quý Đôn - Lai Châu lần 1
- Đề thi thử THPT Quốc gia môn Toán năm 2019 Sở GD&ĐT Bình Phước
Trên đây VnDoc đã giới thiệu tới bạn đọc Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Văn Giang - Hưng Yên lần 1. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Hóa học, Thi thpt Quốc gia môn Vật Lý, Thi thpt Quốc gia môn Sinh học, Mã trường thpt mà VnDoc tổng hợp và đăng tải.



