Đề thi thử vào lớp 10 môn Toán lần 2 trường THCS Quỳnh Mai, Hà Nội năm học 2022-2023
Đề thi tuyển sinh lớp 10 môn Toán
TRƯỜNG THCS QUỲNH MAI
ĐỀ THI THỬ VÀO 10 – LẦN 2
MÔN TOÁN 9 - Năm học 2021 - 2022
Thời gian làm bài 120 phút không kể giao đề
Ngày thi: 7/05/2022
Lưu ý: - HS không dùng bút xóa trong bài làm
- HS không vẽ hình bằng bút chì, trừ đường tròn.
Bài 1(2,0 điểm):
1) Cho biểu thức:
1
1
x
A
x
-
=
+
với . Tính giá trị của A khi x = 25
2) Cho biểu thức
3 3 4
1
11
x
B
x
xx
+
= - +
-
+-
với . Rút gọn B.
3) Tìm các số hữu tỉ x để P = A. B có giá trị nguyên.
Bài 2 (2,5 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
1) Cho một số có hai chữ số. Biết rằng tổng của các chữ số hàng chục và hai lần
chữ số hàng đơn vị là 12. Nếu đổi chỗ hai chữ số cho nhau thì sẽ được một số
mới lớn hơn số ban đầu 27 đơn vị. Tìm số ban đầu.
2) Một bình nước có dạng hình nón, người ta đo được chiều dài đường sinh của
nó là 13dm, đường kính đáy là 10dm. Hỏi bình đựng nước này đựng đầy được
bao nhiêu lít nước ? ( Bỏ qua bề dày của bình nước, lấy
3,14
)
Bài 3(2,0 điểm)
1) Giải hệ phương trình:
2) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = 2x – m +1 và parabol
(P):
2
yx=
. Tìm tất cả giá trị của m để: (d) cắt (P) tại hai điểm phân biệt có hoành
độ
12
;xx
thỏa mãn
3 3 2 2
1 2 1 2
15x x x x+ + =
Bài 4 (3 điểm): Cho nửa đường tròn (O; R), đường kính AB. Tiếp tuyến Ax tại A
(Ax thuộc nửa mặt phẳng chứa nửa đường tròn), lấy điểm C thuộc tia Ax. Từ C kẻ
tiếp tuyến CD với nửa đường tròn (O) tại D. AD giao OC tại E.
1) Chứng minh: Tứ giác ACDO nội tiếp.
2) Chứng minh: AD
2
= 4CE.EO
3) Tiếp tuyến tại B với nửa đường tròn cắt AD tại K và cắt CD tại Q, AQ giao BC
tại F, DF giao AB tại H. Chứng minh: DF // AC và F là trung điểm DH.
Bài 5 (0,5 điểm): Cho x, y > 0 và . Tìm giá trị nhỏ nhất của biểu thức:
2
91
P x x 3y 9
xy
= − + + + +
ĐỀ CHÍNH THỨC
TRƯỜNG THCS QUỲNH MAI
ĐỀ THI THỬ VÀO 10 – LẦN 2
MÔN TOÁN 9 - Năm học 2021 - 2022
Thời gian làm bài 120 phút
Bài
Câu
Nội dung
Điểm
1
2,0đ
1
0,5
Thay đúng x = 25 (tmđk) vào A
0,25
Tính đúng A =
2
3
0,25
2
1,0
( )( )
3 3 4 3 3 4
1
1 1 1 1
11
xx
B
x
x x x x
xx
++
= - + = + +
-
+ - + -
+-
0,25
( )( ) ( )
( )( )
3 1 3 1 4
11
x x x
xx
+ - + + +
=
+-
0,25
( )( ) ( )( )
2 3 3 3 4 5 4
1 1 1 1
x x x x x
x x x x
+ - + + + + +
=
+ - + -
0,25
( )( )
( )( )
41
4
1
11
xx
x
x
xx
++
+
==
-
+-
với
0,25
3
0,5
ĐK:
1 4 4 3
. . 1
1 1 1 1
x x x
P A B
x x x x
- + +
= = = = +
+ - + +
0,25
Lập luận ra , mà
Tìm được
(tmđk)
0,25
2
2,0đ
1
1,5
Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y
; x, y
N*
Số ban đầu là
xy
=10x+y
Vì tổng các chữ số hàng chục và hai lần chữ số hàng đơn vị là
12 nên ta có pt :
2 12xy+=
(1)
0,25
0,5
Đổi chỗ hai chữ số cho nhau thì sẽ được một số mới là
10yx y x=+
Vì khi đổi chỗ hai chữ số cho nhau thì sẽ được một số mới lớn
hơn số ban đầu 27 đơn vị nên ta có pt:
(2)
Từ (1) và (2) ta có hệ pt
0,25
Giải hệ pt:
ra kết quả:
0,25
Đối chiếu điều kiện và kết luận
25xy =
0,25
2
1,0
ℎ
(dm)
0,5
0, 9.xx
HƯỚNG DẪN CHẤM
Thể tích của hình nón là:
ℎ
Vậy bình đựng nước này đựng được
( )
314 lít
0,5
3
2,0
1
1.0
1) Giải hệ phương trình:
ĐK:
Đặt
0,25
Ta có hệ pt
(tmđk)
0,25
Trả biến . (TMĐK)
0,25
Vậy hệ phương trình có nghiệm (x;y) = (0; 1)
0,25
2
1,0
a) Phương trình hoành độ giao điểm :
2
2 1 0x x m- + - =
(*)
Ta có: ′
0,25
ĐK để (d) cắt (P) tại hai điểm phân biệt có hoành độ
12
;xx
là pt
(*) có hai nghiệm pb <=> ′
0,25
b) Áp dụng hệ thức Viet ta có:
Theo đề bài :
3 3 2 2
1 2 1 2
15x x x x+ + =
0,25
Thay (1), (2) vào (3) ta được:
Kết hợp với ĐK: m < 2 suy ra m = 0 (TM)
0,25
4
3,0
0,25
1
1.0
Chứng minh: Tứ giác ACDO nội tiếp.
Chỉ ra:
0,25
Xét tứ giác ACDO có:
Mà 2 góc đối nhau
0,25
0,25
=> Tứ giác ACDO nội tiếp. (không giải thích góc đối – 0,25đ)
0,25
2
Chứng minh: AD
2
= 4CE.EO
E
D
O
A
B
C
H
K
Q
F
E
D
O
A
B
C
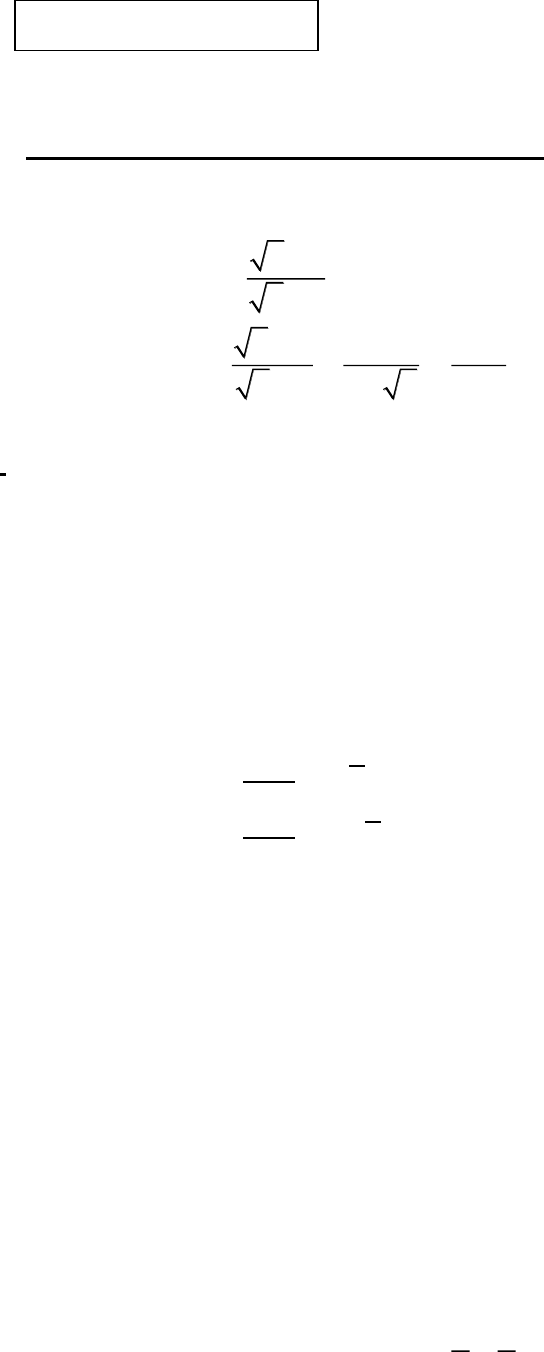
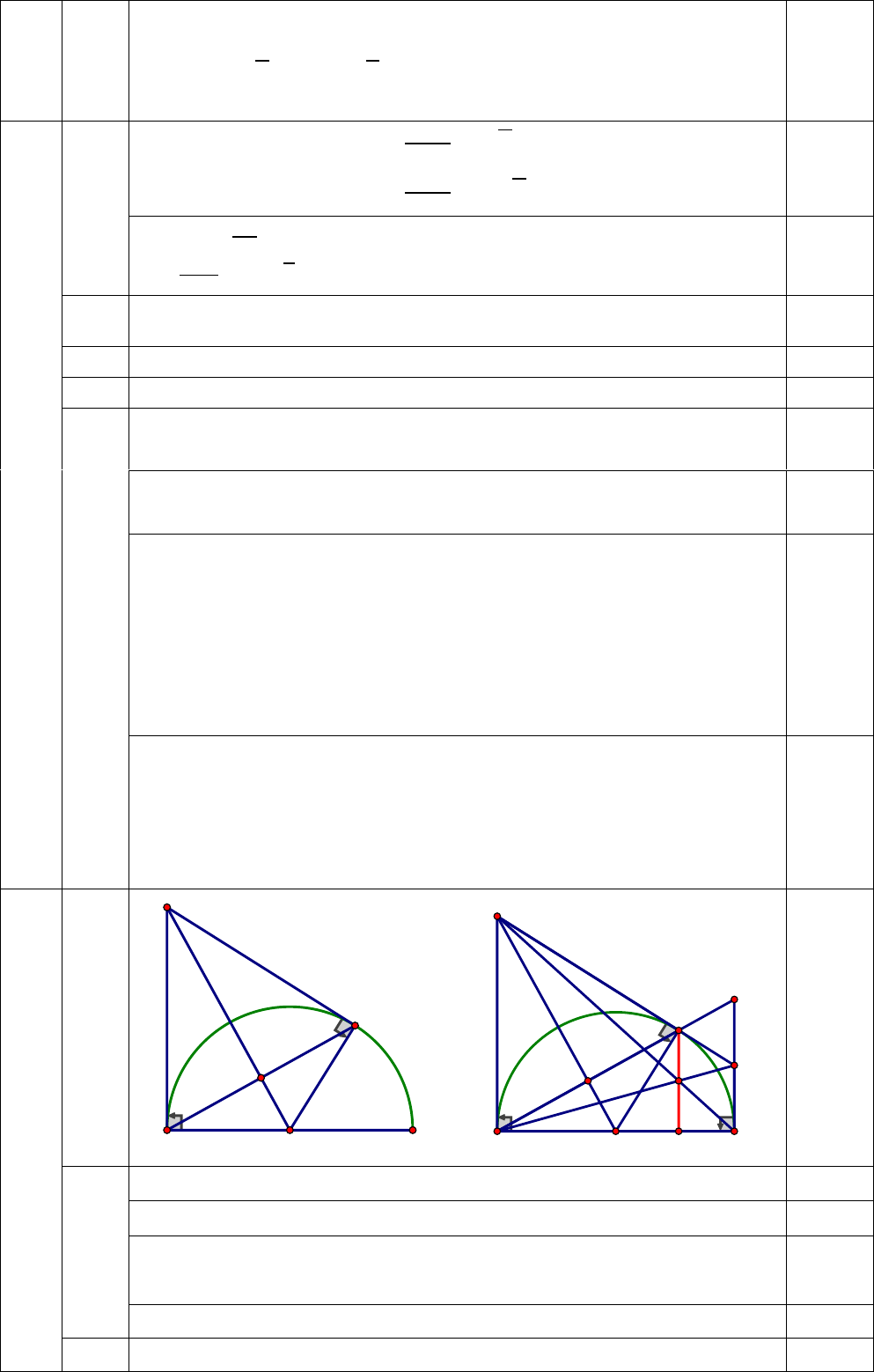
Đề thi tuyển sinh lớp 10 môn Toán lần 2 trường THCS Quỳnh Mai, Hà Nội năm học 2022-2023
Đề thi thử vào lớp 10 môn Toán lần 2 trường THCS Quỳnh Mai, Hà Nội năm học 2022-2023 vừa được VnDoc.com sưu tầm và xin gửi tới bạn đọc. Đây là tài liệu tham khảo giúp bạn đọc có thêm nhiều tài liệu để ôn tập thật tốt cho kì thi tuyển sinh vào lớp 10 sắp tới. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây nhé.
- Đề thi thử vào lớp 10 môn Toán trường THCS Nguyễn Thị Định, Bà Rịa - Vũng Tàu năm học 2022-2023
- Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Ninh Bình năm học 2022-2023
Đề thi thử vào lớp 10 môn Toán lần 2 trường THCS Quỳnh Mai, Hà Nội năm học 2022-2023 được biên soạn theo hình thức đề tự luận. Đề được tổng hợp gồm có 5 câu hỏi tự luận, thí sinh làm bài trong thời gian 120 phút. Đề có đáp án và lời giải chi tiết kèm theo.
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Đề thi thử vào lớp 10 môn Toán lần 2 trường THCS Quỳnh Mai, Hà Nội năm học 2022-2023. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của đề thi rồi đúng không ạ? Mong rằng qua bài viết bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 9 nhé. Mời các bạn cùng tham khảo thêm tài liệu các môn Ngữ văn lớp 9, Tiếng Anh lớp 9...
