Tính diện tích hình tròn và diện tích quạt tròn
Diện tích hình tròn - Diện tích hình quạt tròn
Tài liệu tính diện tích hình tròn và diện tích quạt tròn là một dạng toán thường gặp trong các đề thi tuyển sinh vào lớp 10 môn Toán gần đây. Tài liệu được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
I. Một số kiến thức cần nhớ khi tính diện tích hình tròn và diện tích quạt tròn
1. Công thức tính diện tích hình tròn
Hình tròn có bán kính R có diện tích được tính bởi công thức là:
\(S = \pi {R^2}\)
2. Cách tính diện tích hình quạt tròn
Trong hình tròn bán kính R, diện tích hình quạt a0 được tính theo công thức:
\(S = \frac{{\pi {R^2}a}}{{360}} = \frac{{l\pi }}{2}\),
trong đó l là độ dài cung a0 của hình quạt
Tính diện tích hình tròn Trực tuyến
Mời bạn nhập số liệu: Bán kính và Đường kính rồi nhấn vào nút Tính toán để nhận kết quả!
II. Bài tập ví dụ cho các bài tập về tính diện tích hình tròn và diện tích quạt tròn
Bài 1: Tính diện tích hình quạt tròn có bán kính bằng 1 cm và cung 600
Lời giải chi tiết:
+ Hình quạt cung 600 có diện tích là: \(\frac{{\pi .{1^2}.60}}{{360}} = \frac{\pi }{{60}}\)cm2
Bài 2: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Kẻ đường cao AD và đường kính AK. Hạ BE và CF vuông góc với AK
a, Chứng minh ABDE và ACFD là các tứ giác nội tiếp
b, Chứng minh DF // BK
c, Cho góc ABC bằng 600, bán kính R = 4 cm. Tính diện tích hình quạt tròn giới hạn bởi OC, OK và cung nhỏ CK
Lời giải chi tiết:
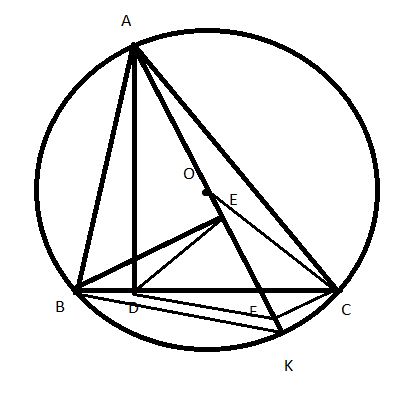
a, Có AD là đường cao của tam giác ABC nên \(\widehat {ADB} = {90^0}\)
• Có BE vuông góc với AK nên \(\widehat {AEB} = {90^0}\)
Xét tam giác ABE vuông tại E nên A, B, E thuộc đường tròn đường kính AB
Tam giác ADB vuông tại D nên A, B, D thuộc đường tròn đường kính AB
Do đó A, B, D, E cùng thuộc một đường tròn hay ABDE là tứ giác nội tiếp.
• Có CF vuông góc với AK nên \(\widehat {CFA} = {90^0}\)
• Xét tam giác ACF vuông tại F nên A, C, F thuộc đường tròn đường kính AC
Tam giác ADC vuông tại D nên A, C, D thuộc đường tròn đường kính AC
Do đó A, C, F, D cùng thuộc một đường tròn hay ACFD là tứ giác nội tiếp.
b, Có ADFC là tứ giác nội tiếp nên \(\widehat {CDF} = \widehat {CAK}\) (góc nội tiếp cùng chắn cung CF)
Trong đường tròn (O), có \(\widehat {CBK} = \widehat {CAF}\)(góc nội tiếp cùng chắn cung CK)
Suy ra \(\widehat {CDF} = \widehat {CBK}\left( { = \widehat {CAK}} \right)\)
Mà hai góc ở vị trí đồng vị
Suy ra DF // BK
c, Ta có \(\widehat {ABC}\) là góc nội tiếp chắn cung AC và \(\widehat {AOC}\) là góc ở tâm chắn cung AC
Suy ra \(\widehat {ABC} = \frac{1}{2}\widehat {AOC} \Rightarrow \widehat {AOC} = {120^0}\)
• Có \(\widehat {AOC}\) và \(\widehat {COK}\) là hai góc kề bù nên \(\widehat {COK} = {180^0} - {120^0} = {60^0}\)
• Diện tích quạt tròn giới hạn bởi OC, OK và cung nhỏ CK là:
\(S = \frac{{\pi .16.60}}{{360}} = \frac{8}{3}\pi\) cm2
III. Bài tập tự luyện các bài toán về tính diện tích hình tròn và diện tích quạt tròn
Bài 1: Trên đường tròn tâm O bán kính bằng 12 cm, vẽ dây AB = 12 cm. Tính diện tích hình quạt tạo bởi hai bán kính OA, OB và cung nhỏ AB
Bài 2: Cho tam giác ABC nội tiếp trong nửa đường tròn đường kính AB, biết góc A bằng 600. Tính diện tích hình quạt BOC (với O là trung điểm của cạnh AB)
Bài 3: Cho đường tròn (O; R). Từ điểm P ở ngoài đường tròn, kẻ các tiếp tuyến PA, PB (A, B là hai tiếp điểm) và kẻ đường kính AC của đường tròn
a, Chứng minh PO // BC
b, Cho OP = 2R. Tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
Bài 4: Từ một điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC và cát tuyến AMN của đường tròn đó. Cho góc BAC có số đo bằng 600, OB = 2 cm
a, Chứng minh tứ giác ABOC nội tiếp
b, Tính số đo của góc BOA
c, Tính diện tích hình quạt OBNC
Bài 5: Cho đường tròn (O) có bán kính bằng 6 cm. Tính:
a, Tính độ dài đường tròn
b, Độ dài cung AB, biết góc AOB bằng 300
c, Tính diện tích hình tròn
Bài 6: Cho tam giác ABC nội tiếp trong nửa đường tròn, đường kính AB. Biết góc A bằng 600, AC = 6 cm. Tính diện tích hình quạt tròn BOC (với O là trung điểm của AB)
Bài 7: Diện tích cảu hình tròn bằng 12,56 m2. Tính chu vi đường tròn đó.
Bài 8: Cho đường tròn (O) có bán kính 3 cm. Trên đường tròn lấy hai điểm A, B sao cho:
a, Tính độ dài của cung nhỏ AB và cung lớn AB
b, Tính diện tích hình quạt tròn OAC, cung 700
c, Tính diện tích của hình quạt tròn OAB khi số đo của cung nhỏ AB bằng 1400
Bài 9: Cho đường tròn (O) có chu vi 12 cm
a, Tính diện tích hình tròn đó
b, Tính diện tích hình quạt tròn, biết số đo cung là 200
Bài 10: Tính diện tích hình viên phân giới hạn bởi cung AB và dây AB.
-------------------
