Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Xuân Trường, Nam Định

Đề thi thử THPT Quốc gia môn Toán

Nhằm giúp các bạn thử sức trước kì thi THPT Quốc gia 2015, VnDoc xin giới thiệu đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Xuân Trường, Nam Định có đáp án kèm theo. Hi vọng tài liệu này giúp các bạn ôn luyện môn Toán hiệu quả và đạt kết quả cao trong kì thi tới. Mời các bạn tham khảo.

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Việt Yên 2, Bắc Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO NAM ĐỊNH TRƯỜNG THPT XUÂN TRƯỜNG ĐỀ CHÍNH THỨC

ĐỀ THI THỬ THPTQG- LẦN 1 NĂM HỌC: 2015-2016 Môn: TOÁN Thời gian làm bài: 150 phút, không kể thời gian phát đề

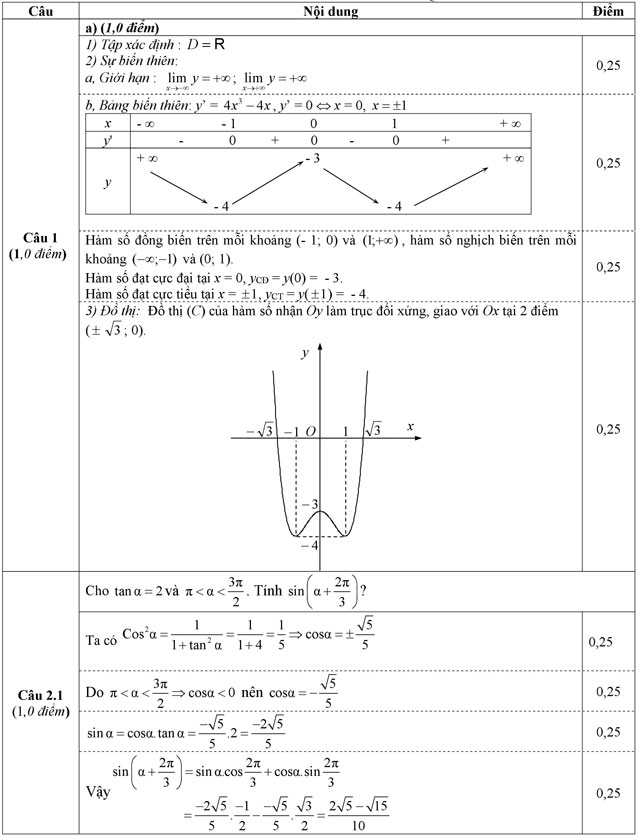
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x⁴ - 2x² - 3.

Câu 2 (2,0 điểm).

a) Cho tanα = 2 và π < α < 3π/2. Tính sin(α + 3π/2).

b) Giải phương trình: cosx + sin4x - cos3x = 0.

Câu 3 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 1/2].

Câu 4 (1,0 điểm). Giải phương trình 2.4^x + 6^x = 9^x.

Câu 5 (1,0 điểm). Trong đợt thi học sinh giỏi của tỉnh Nam Định trường THPT Xuân Trường môn Toán có 5 em đạt giải trong đó có 4 nam và 1 nữ, môn Văn có 5 em đạt giải trong đó có 1 nam và 4 nữ, môn Hóa học có 5 em đạt giải trong đó có 2 nam và 3 nữ, môn Vật lí có 5 em đạt giải trong đó có 3 nam và 2 nữ. Hỏi có bao nhiêu cách chọn mỗi môn một em học sinh để đi dự đại hội thi đua? Tính xác suất để có cả học sinh nam và nữ để đi dự đại hội?

Câu 6 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết SD = 2a√3 và góc tạo bởi đường thẳng SC với mặt phẳng (ABCD) bằng 30⁰. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ điểm B đến mặt phẳng (SAC).

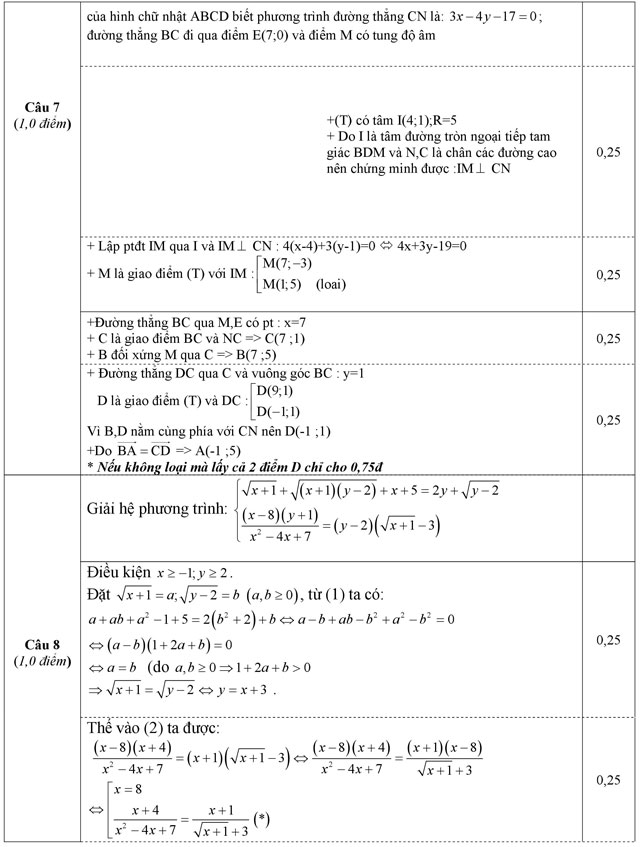
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD. Gọi M là điểm đối xứng của B qua C và N là hình chiếu vuông góc của B trên MD. Tam giác BDM nội tiếp đường tròn (T) có phương trình: (x - 4)² + (y - 1)² = 25. Xác định tọa độ các đỉnh của hình chữ nhật ABCD biết phương trình đường thẳng CN là: 3x - 4y - 17 = 0; đường thẳng BC đi qua điểm E(7; 0) và điểm M có tung độ âm.

Câu 8 (1,0 điểm). Giải hệ phương trình: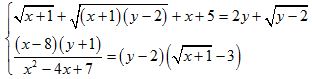

Câu 9 (1,0 điểm). Cho x, y, z ∈ [0; 2] thỏa mãn x + y + z = 3. Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán