Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Bạc Liêu - Ninh Bình lần 2
Đề minh họa Toán 2019 có đáp án
SỞ GDĐT NINH BÌNH
TRƯỜNG THPT
NINH BÌNH - BẠC LIÊU
ĐỀ KIỂM TRA CHẤT LƯỢNG LỚP 12
NĂM HỌC: 2018 - 2019
Môn: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
(Đề thi gồm 50 câu TNKQ, trong 6 trang)
Họ và tên: ... .. .. .. .. .. ... .. .. .. .. .. .. .... .. .. .. .. .. ..Số báo danh: .. .. .. .. .. .. .. Mã đề : 131
Câu 1. Họ nguyên hàm của hàm số f (x) = x + sin x là
A. x
2
− cos x + C. B. 1 + cos x + C. C.
x
2
2
− cos x + C. D.
x
2
2
+ cos x + C.
Câu 2. Thể tích của khối hình hộp chữ nhật có các kích thước là 2a, 3a, 5a là
A. 10a
3
. B. 6a
3
. C. 15a
3
. D. 30a
3
.
Câu 3.
Điểm M trong hình bên là điểm biểu diễn của số phức z.
Mệnh đề nào sau đây đúng?
A. Số phức z có phần thực là 3 và phần ảo là −4i.
B. Số phức z có phần thực là 3 và phần ảo là −4.
C. Số phức z có phần thực là −4 và phần ảo là 3i.
D. Số phức z có phần thực là −4 và phần ảo là 3.
O
x
y
−4
M
3
Câu 4. Cho hàm số y = f(x) có bảng biến thiên trên đoạn [−2; 3] như hình bên dưới. Gọi M và m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [−1; 3]. Giá trị của biểu
thức M − m là
x
f
0
(x)
f(x)
−∞
−2 −1
1 3
+∞
+
0
− +
00
11
−2−2
5
A. 7. B. 5. C. 3. D. −1.
Câu 5. Trong không gian Oxyz, cho hai điểm A(2; −4; 3) và B(2; 2; 7). Trung điểm của đoạn AB
có tọa độ là
A. (2; −1; 5). B. (4; −2; 10). C. (1; 3; 2). D. (2; 6; 4).
Câu 6. Trong không gian với hệ toạ độ Oxyz, hình chiếu của điểm M(1; −3; −5) trên mặt phẳng
(Oyz) có toạ độ là
A. (0; −3; 5). B. (0; −3; 0). C. (1; −3; 0). D. (0; −3; −5).
Câu 7. Cho các số thực dương a, b với a 6= 1. Khẳng định nào sau đây là đúng?
A. log
a
2
(ab) =
1
4
log
a
b. B. log
a
2
(ab) =
1
2
log
a
b.
C. log
a
2
(ab) =
1
2
+
1
2
log
a
b. D. log
a
2
(ab) = 2 + 2 log
a
b.
Câu 8.
Cho hàm số y = f(x) có bảng biến thiên như
hình vẽ. Hàm số y = f(x) nghịch biến trên
khoảng nào dưới đây?
A. (−2; 4). B. (−1; 3).
C. (3; +∞). D. (−∞; −1).
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
44
−2−2
+∞+∞
Trang 1/6 - Mã đề 131

Câu 9. Cho hàm số f(x) thỏa mãn f (1) = 12, f
0
(x) liên tục trên đoạn [1; 4] và
4
Z
1
f
0
(x) dx = 17.
Tính f(4).
A. 26. B. 29. C. 9. D. 5.
Câu 10. Cho hàm số y = f (x) xác định trên R và có bảng xét dấu đạo hàm như sau:
x
y
0
−∞
x
1
x
2
x
3
+∞
−
0
+ −
0
+
Khi đó số điểm cực trị của đồ thị hàm số y = f (x) là
A. 1. B. 4. C. 2. D. 3.
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho véc-tơ
−→
x = 3
−→
j − 2
−→
k +
−→
i . Tìm tọa độ của
véc-tơ
−→
x .
A.
−→
x = (3; −2; 1). B.
−→
x = (1; 2; 3). C.
−→
x = (1; 3; −2). D.
−→
x = (1; −2; 3).
Câu 12. Phương trình 4
x
− 2
x+2
+ 3 = 0 có bao nhiêu nghiệm thực?
A. 0. B. 3. C. 1. D. 2.
Câu 13. Cho hàm số y = f (x) xác định và có đạo hàm trên R \ {±1}. Hàm số có bảng biến thiên
như hình vẽ dưới đây.
x
y
0
y
−∞
−1
0 1
+∞
+ −
0
+ +
−4−4
2
+∞
−3−3
+∞
−∞
44
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 2 . B. 1 . C. 4 . D. 3 .
Câu 14. Cho hai tích phân
5
Z
−2
f(x) dx = 8 và
5
Z
−2
g(x) dx = −3. Tính
5
Z
−2
[f(x) − 4g(x) − 1] dx
A. I = 13. B. I = 27. C. I = −11. D. I = 3.
Câu 15. Cho log
a
b = 2, log
a
c = 3. Giá trị của biểu thức P = log
a
b
2
c
3
bằng
A.
4
9
. B. 13. C. −5. D. 36.
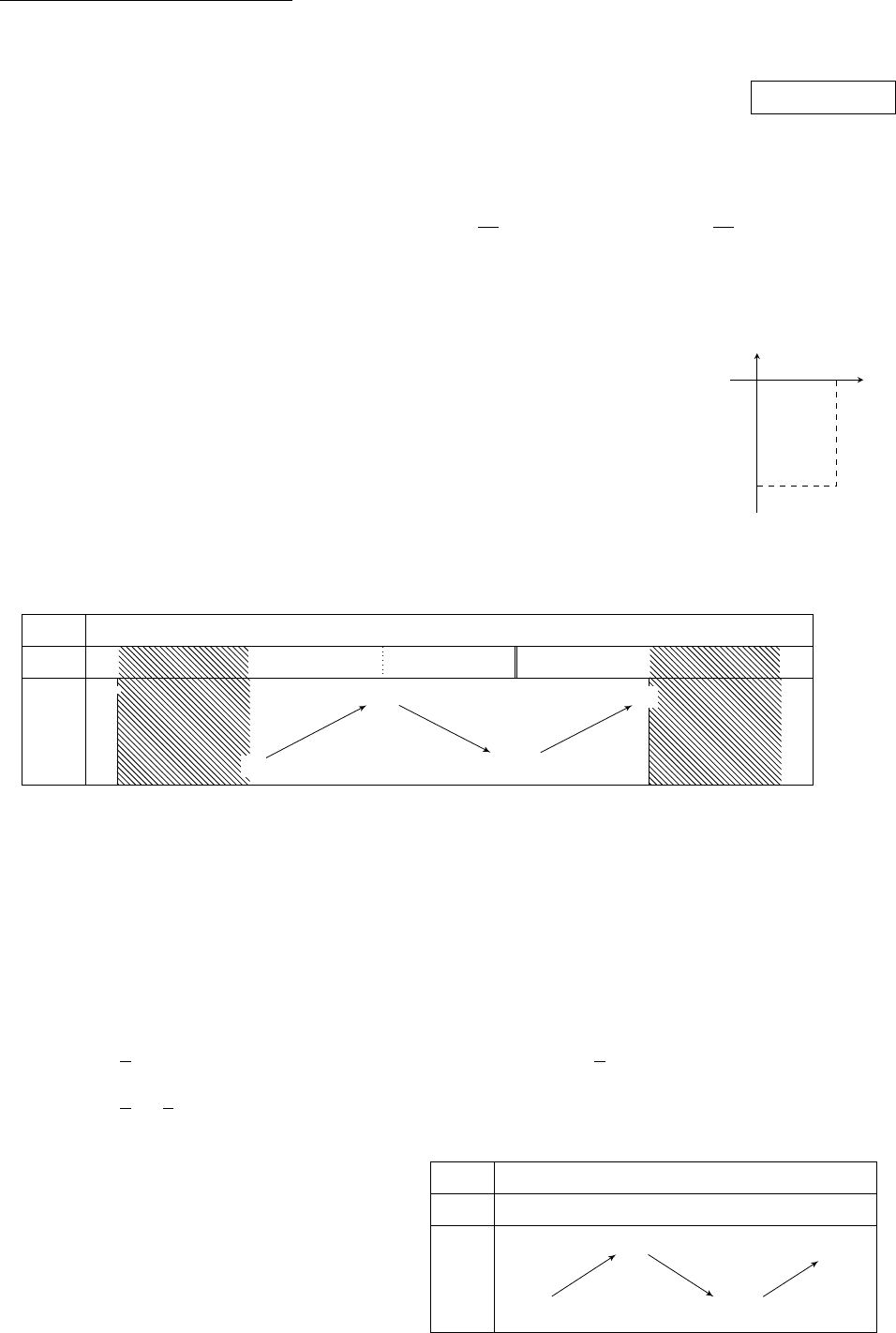
Câu 16. Diện tích của hình phẳng (H) giới hạn bởi đồ thị của hàm số y = f (x), trục hoành và hai
đường thẳng x = a, x = b (a < b) (phần tô đậm trong hình vẽ) tính theo công thức
A. S =
b
Z
a
f(x) dx
.
B. S =
c
Z
a
f(x) dx +
b
Z
c
f(x) dx.
C. S =
b
Z
a
f(x) dx.
D. S = −
c
Z
a
f(x) dx +
b
Z
c
f(x) dx.
O
x
y
y = f(x)
x = a
x = b
c
Trang 2/6 - Mã đề 131
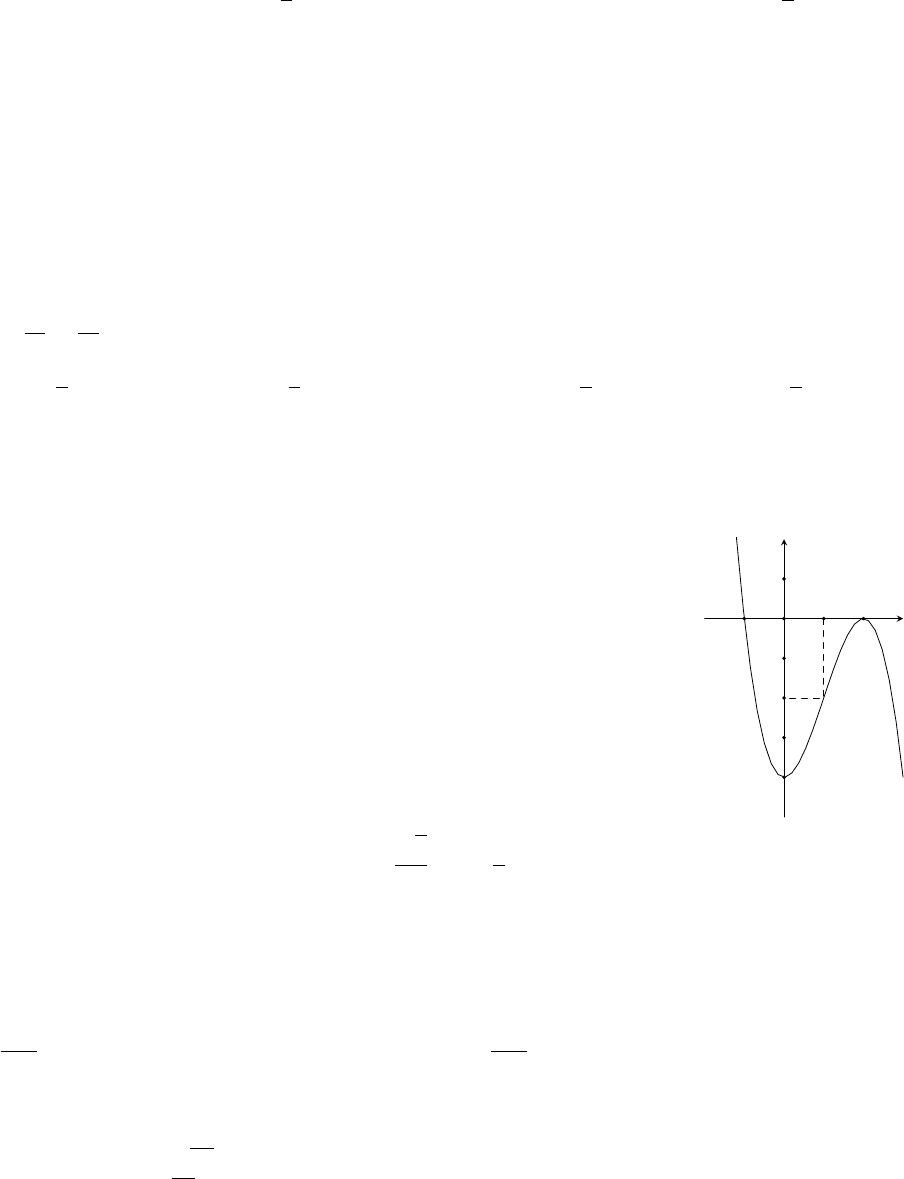
Câu 17. Cho cấp số nhân (u
n
) có u
2
= 2, u
4
= 4. Giá trị của u
10
bằng
A. 32. B. 16
√
2. C. 10. D. 32
√
2.
Câu 18. Một hình hộp chữ nhật có ba kích thước a, b, c nội tiếp một mặt cầu. Tính diện tích S
của mặt cầu đó.
A. S = 16(a
2
+ b
2
+ c
2
)π. B. S = (a
2
+ b
2
+ c
2
)π.
C. S = 4(a
2
+ b
2
+ c
2
)π. D. S = 8(a
2
+ b
2
+ c
2
)π.
Câu 19. Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A(1; −1; 1), B(3; 3; −1). Lập phương
trình mặt phẳng trung trực của đoạn AB.
A. x + 2y − z − 4 = 0. B. x + 2y + z − 4 = 0.
C. x + 2y − z + 2 = 0. D. x + 2y − z − 3 = 0.
Câu 20. Gọi z
1
, z
2
là hai nghiệm phức của phương trình 2z
2
− 3z + 4 = 0.
Tính w =
1
z
1
+
1
z
2
+ iz
1
z
2
.
A. w = −
3
4
+ 2i. B. w =
3
4
+ 2i. C. w = 2 +
3
2
i. D. w =
3
2
+ 2i.
Câu 21. Cho hình nón có thể tích bằng V = 36πa
3
và bán kính bằng 3a. Tính độ dài đường cao h
của hình nón đã cho.
A. h = 4a. B. h = 12a. C. h = 5a. D. h = 2a.
Câu 22. Đồ thị sau đây là của hàm số nào?
A. y = −x
3
− 3x
2
− 4. B. y = −x
3
+ 3x
2
− 4.
C. y = x
3
− 3x − 4. D. y = x
3
− 3x
2
− 4.
x
y
−1
1 2
−1
−2
−3
−4
1
O
Câu 23. Tập nghiệm của bất phương trình
√
3
2
!
x
>
3
4
là
A. (−∞; −2). B. (2; +∞). C. (−2; +∞). D. (−∞; 2).
Câu 24. Cho hình vuông ABCD biết cạnh bằng a. Gọi I, K lần lượt là trung điểm của AB, CD.
Tính diện tích xung quanh của hình trụ tròn xoay khi cho hình vuông ABCD quay quanh IK một
góc 360
◦
.
A. 2
πa
2
3
. B. 2πa
2
. C.
πa
2
3
. D. πa
2
.
Câu 25. Trong không gian với hệ trục tọa độ Oxyz cho (S) : x
2
+ y
2
+ z
2
−2x + 4y −4z −25 = 0.
Tìm tâm I và bán kính R của mặt cầu (S).
A. I(−2; 4; −4); R =
√
29. B. I(−1; 2; −2); R = 5.
C. I(1; −2; 2); R =
√
34. D. I(1; −2; 2); R = 6.
Câu 26. Số cách xếp 5 người vào 5 vị trí ngồi thành hàng ngang là
A. 120. B. 24. C. 15. D. 25.
Câu 27. Cho hàm số f(x) liên tục trên R và có đạo hàm f
0
(x) = x
3
(x + 1)
2
(x − 2). Hỏi hàm số
f(x) có bao nhiêu điểm cực trị?
A. 0. B. 1. C. 2. D. 3.
Câu 28. Cho hàm số y = f(x) có đạo hàm f
0
(x) = x
2
(x − 9)(x − 4)
2
. Khi đó, hàm số y = f (x
2
)
đồng biến trên khoảng nào?
A. (−∞; −3) ∪ (0; 3). B. (−∞; −3).
C. (−2; 2). D. (3; +∞).
Trang 3/6 - Mã đề 131
Đề thi thử Toán THPT Quốc gia năm 2019
VnDoc xin giới thiệu tới bạn đọc Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Bạc Liêu - Ninh Bình lần 2. Nội dung tài liệu gồm 50 câu hỏi trắc nghiệm, thời gian làm bài 90 phút, đề thi có đáp án. Mời các bạn học sinh tham khảo.
- Đề thi thử THPT Quốc gia môn Toán năm 2019 Sở GD&ĐT Hà Nội
- Đề thi thử THPT Quốc gia môn Ngữ văn năm 2019 Sở GD&ĐT Hà Nội
- Đề thi thử THPT Quốc gia môn Toán năm 2019 Sở GD&ĐT Bình Phước
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Thanh Chương 1 - Nghệ An lần 2
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT 19-5 Kim Bôi - Hòa Bình
- Đề thi thử THPT Quốc gia môn Toán năm 2019 Sở GD&ĐT Bắc Giang
- Đề thi thử THPT Quốc gia môn Toán năm 2019 hội 8 trường Chuyên Đồng Bằng Sông Hồng lần 2
- Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Chuyên Lê Khiết - Quảng Ngãi lần 1
Trên đây VnDoc đã giới thiệu tới bạn đọc Đề thi thử THPT Quốc gia môn Toán năm 2019 trường THPT Bạc Liêu - Ninh Bình lần 2. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Hóa học, Thi thpt Quốc gia môn Vật Lý, Thi thpt Quốc gia môn Sinh học, Mã trường thpt mà VnDoc tổng hợp và đăng tải.



