Cho tứ giác có:
. Tính số đo góc ngoài tại đỉnh
.
Ta có:
Khi đó số đo góc ngoài tại đỉnh là:
Vndoc.com xin gửi tới bạn đọc bài viết Bài tập Toán lớp 8: Tứ giác sách Chân trời sáng tạo. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé!
Cho tứ giác có:
. Tính số đo góc ngoài tại đỉnh
.
Ta có:
Khi đó số đo góc ngoài tại đỉnh là:
Xác định x và y trong hình vẽ sau:
Ta có: , theo tính chất một đường thẳng cắt hai đường thẳng song song ta có:
(hai góc trong cùng phía)
(hai góc đồng vị).
Tìm giá trị x trong hình vẽ sau:
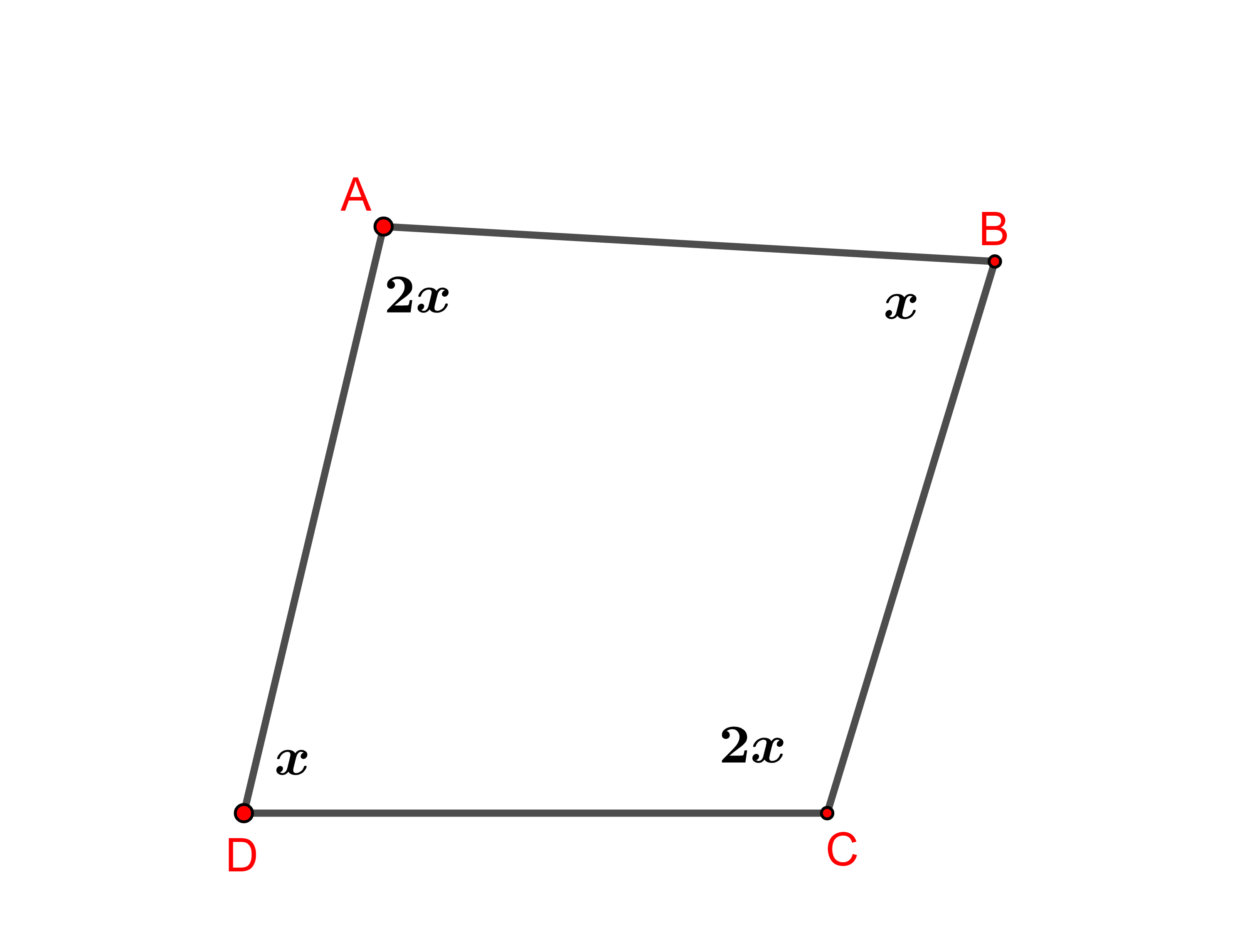
Ta có: Tổng 4 góc của một tứ giác bằng khi đó:
Cho tứ giác có
. Khi đó tổng số đo
bằng bao nhiêu?
Ta có: Tổng 4 góc của một tứ giác bằng khi đó:
Nối các đáp án phù hợp
Cho tứ giác ABCD biết ![]() . Số đo các góc
. Số đo các góc ![]() lần lượt là:
lần lượt là:
Ta có:
Mặt khác
Cho tứ giác ABCD có: . Các tia phân giác của góc
và góc
cắt nhau tại điểm
. Biết rằng
. Tính số đo góc
.
Hình vẽ minh họa
Xét tam giác ta có:
(Vì )
Xét tứ giác có:
, do đó:
Vậy . Theo đề bài
Mặt khác
Do đó
Tứ giác có tối đa bao nhiêu góc tù?
Nếu 4 góc tứ giác đều tù
=> Tổng 4 góc lớn hơn (Vô lí)
(Vì tổng 4 góc trong 1 tứ giác bằng )
- Nếu 3 góc tù và 1 góc nhọn
Tổng 3 góc tù lớn hơn
=> Góc còn lại của tứ giác nhỏ hơn (thỏa mãn)
Vậy 1 tứ giác có thể có nhiều nhất 3 góc tù.
Cho tứ giác ABCD có . Các tia phân giác ngoài tại đỉnh
cắt nhau tại
. Tính số đo của góc
.
Hình vẽ minh họa
Xét tứ giác ABCD có
Xét tam giác có:
Cho tứ giác có
. Tính số đo góc
?
Ta có:
Tổng 4 góc của một tứ giác bằng khi đó:
Tìm giá trị x trong hình vẽ:

Ta có:
Cho tứ giác có
; số đo góc
gấp đôi số đo góc
, số đo góc
gấp đôi số đo góc
. Số đo các góc
của tứ giác lần lượt là:
Ta có:
(*)
Mà
Các số đo nào dưới đây chỉ bốn góc của một tứ giác?
Dựa vào tính chất tổng bốn góc của một tứ giác bằng 3600 ta suy ra dãy số chỉ bốn góc của một tứ giác là:
Vì
Cho tứ giác ABCD biết ;
;
. Số đo các góc
lần lượt là:
Từ giả thiết ta có:
Vì
Cho tứ giác ABCD có . Phân giác trong của các góc
cắt nhau tại
, biết
. Khi đó tỉ số
bằng:
Hình vẽ minh họa

Theo bài ra ta có:
Gọi M là trung điểm của cạnh CD. Khi đó:
Vậy tam giác DEM đều
Cho tứ giác biết:
. Số đo các góc
lần lượt là:
Ta có:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
