Đề thi chọn học sinh giỏi lớp 11 môn Toán năm 2018 - 2019 trường THPT Thị xã Quảng Trị
Đề thi HSG Toán 11 có đáp án

SỞ GD&ĐT QUẢNG TRỊ KỲ THI CHỌN HSG VĂN HÓA LỚP 10, 11
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Khóa thi ngày 03 tháng 4 năm 2019
Môn thi: Toán lớp 11
Thời gian làm bài: 180 phút, không kể thời gian giao đề
Câu I (5,0 điểm).
1. Giải phương trình:
22
sin 3 cos2 sin 0.xx x
2. Cho
1
x
và
2
x
là hai nghiệm của phương trình:
2
30xxa,
3
x
và
4
x
là hai nghiệm của
phương trình:
2
12 0xxb. Biết rằng
1234
,,,
x
xxx theo thứ tự lập thành một cấp số nhân. Hãy
tìm
,ab.
Câu II (3,0 điểm).
1. Cho
k
là số tự nhiên thỏa mãn:
5 2014k
.
Chứng minh rằng:
01155
5 2014 5 2014 5 2014 2019
...
kk kk
CC CC CC C
.
2. Tìm m để phương trình sau có nghiệm thực:
22 422
1122111mx x x x x .
Câu III (3,0 điểm).
Cho dãy số
n
u được xác định bởi:
11
2
sin
sin1;
nn
n
uuu
n
, với ,2nn .
Chứng minh rằng dãy số
n
u xác định như trên là một dãy số bị chặn.
Câu IV (3,0 điểm). Cho tứ diện
A
BCD có tam giác
A
BC đều cạnh bằng a và tam giác BCD cân
tại
D
với
5
2
a
DC
.
1. Chứng minh rằng:
A
DBC
.
2. Gọi G là trọng tâm tam giác BCD , tính cosin góc giữa hai đường thẳng
A
G và CD , biết
góc giữa hai mặt phẳng
()
A
BC
và
()BCD
bằng
0
30 .
Câu V (3,0 điểm). Trong mặt phẳng tọa độ Oxy , cho tam giác
A
BC với
(2;1)A
,
(1; 2)B
, trọng
tâm
G của tam giác nằm trên đường thẳng 2 0
x
y. Tìm tọa độ đỉnh C biết diện tích tam giác
ABC bằng
27
2
.
Câu VI (3,0 điểm). Cho các số dương ,,abc thỏa mãn:
222
3abc. Chứng minh rằng:
2
22 22 22
444
1113abc
ab bc ca
. Đẳng thức xảy ra khi nào?
-----------------HẾT---------------------
Thí sinh không được sử dụng tài liệu và MTCT.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:
……………………………….Số báo danh:……………….
ĐỀ THI CHÍNH THỨC
(Đề có 01 trang)

Huớng dẫn chấm – Toán 11
Câu Nội dung Điểm
Câu I.
(5đ)
Giải phương trình:
22
sin 3 cos 2 sin 0.xx x
1. (3đ)
22
sin 3 cos 2 sin 0xx x (1)
Ta có:
sin3 (1 2cos 2 )sinx.xx
22
22
(1) ((1 2 cos 2 ) cos2 1) sin 0
(1 os2x)(1+4cos 2 )sin 0
sin 0
cos2x=-1
2
xx x
cxx
x
k
x
1.0đ
1.0đ
1.0đ
2. (2đ)
Cho
1
x
và
2
x
là hai nghiệm của phương trình:
2
30xxa
,
3
x
và
4
x
là hai
n
ghiệm của phương trình:
2
12 0xxb. Biết rằng
1234
,,,
x
xxx theo thứ tự lập
t
hành
m
ột cấp số nhân. Hãy tìm ,ab.
Gọi q là công bội của CSN
23
2131 41
;;
x
xq x xq x xq
Theo viet ta có:
1
12
12
12
2
34
1
34
34
(1 ) 3
3
12
(1 ) 12
xq
xx
xx a
xx a
xx
xq q
xx b
xx b
Suy ra
2
4q
+ q = 2
1
1x
, giải ra được a = 2, b = 32
+q = -2
1
3x, giải ra được a = -18, b = -288
1.0đ
1.0đ
Câu II.
(3đ)
1. (1.5đ) Cho k là số tự nhiên thỏa mãn: 5 2014k
Chứng minh rằng:
01155
5 2014 5 2014 5 2014 2019
...
kk kk
CC CC CC C
Ta có:
5 2014 2019
(1 ) (1 ) (1 )xx x
5 01 22334455
555555
2014 0 1 2013 2013 2014 2014
2014 2014 2014 2014 2014
2019 0 1 2018 2018 2019 2019
2019 2019 2019 2019 2019
(1 )
(1 ) ... ...
(1 ) ... ...
kk
kk
MxCCxCxCxCxCx
NxCCxCx CxCx
PxCCxCx CxCx
Ta có hệ số của x
k
trong P là
2019
k
C
, P = M.N
Mà số hạng chứa x
k
trong M.N là :
0 1 11 22 22 3333 44 44 5555
5 2014 5 2014 5 2014 5 2014 5 2014 5 2014
kk kk kk kk kk kk
CC x CxC x C xC x CxC x CxC x CxC x
Vậy :
01155
5 2014 5 2014 5 2014 2019
...
kk kk
CC CC CC C
0.5đ
0.5đ
0.5đ
2. (1.5đ) Tìm m để phương trình sau có nghiệm thực:
22 422
1122111mx x x x x
ĐK: 11
x
, Đặt
22
11tx x, t liên tục trên
1;1 và 0t
24
221 2 0;2txt
Pttt:
2
2
2
(2) 2
2
tt
mt t t m
t
Xét
2
2
() ; 0; 2
2
tt
ft t
t
, ()
f
t liên tục trên 0; 2
2
2
4
'( ) 0, 0; 2
(2)
tt
ft t
t
0.5đ
0.5đ
()
f
t nghịch biến trên 0; 2
Vậy pt đã cho có nghiệm thực khi
(2) 2 1 1 (0)
f
mf
0.5đ
Câu III.
(3đ)
Cho dãy số
n
u được xác định bởi:
11
2
sin
sin1;
nn
n
uuu
n
, với mọi
,2nn
. Chứng minh rằng dãy số
n
u
xác định như trên là một dãy số bị
chặn.
Ta có:
*
22 2
11 1
... 2,
12
nN
n
, vì
22 2
11 1 1 1 1
... 1 ...
1 2 1.2 2.3 .( 1)
111 1 1 1
1 1 ... 2 2
223 1
nnn
nn n
Bằng qui nạp ta CM được:
22 2
sin1 sin 2 sin
...
12
n
n
u
n
Suy ra :
*
22 2 22 2
11 1 11 1
2 ... ... 2,
12 12
n
unN
nn
Vậy dãy số
n
u xác định như trên là một dãy số bị chặn.
1.0đ
1.0đ
1.0đ
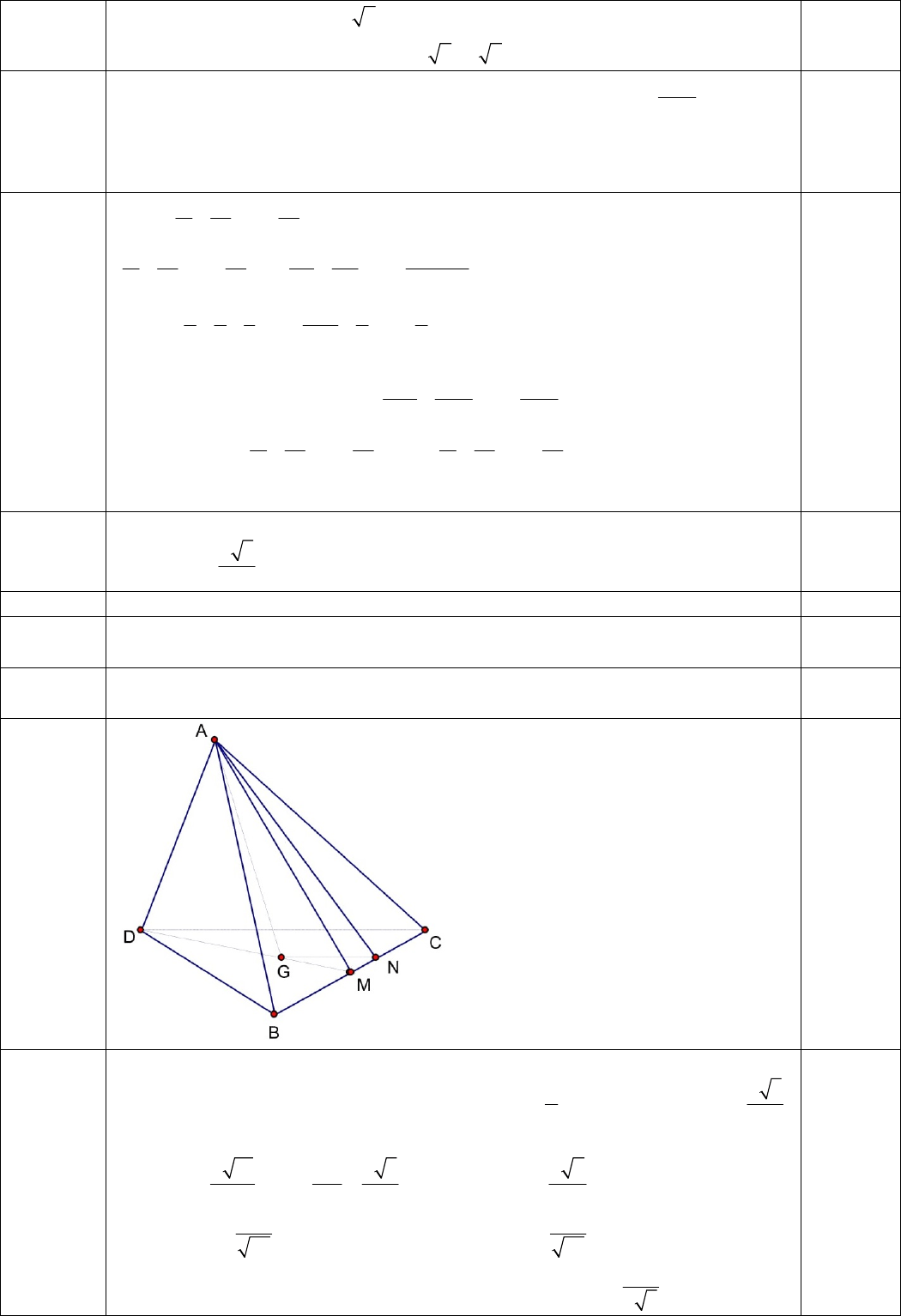
Câu IV.
(3đ)
Cho tứ diện ABCD có tam giác ABC đều cạnh bằng a và tam giác BCD cân tại
D với
5
2
a
DC
.
1. (1đ) Chứng minh rằng:
A
DBC .
Gọi M là trung điểm BC, ta có:
A
BC
đều nên
A
MBC
,
DBC
cân nên
() .DM BC BC AMD BC AD
1.0đ
2. (2đ) Gọi G là trọng tâm tam giác BCD, tính cosin góc giữa hai đường thẳng AG và
CD, biết góc giữa hai mặt phẳng (ABC) và (BCD) bằng
0
30 .
Theo gt ta có góc giữa MA và MD bằng 30
0
. Kẻ GN//CD, nối AN
+TH1: góc DAM bằng 30
0
, ta có: ,
3
a
M
Da MG ABC đều nên
3
2
a
AM
.
Áp dụng định lí cosin cho
A
MG
ta có
13 5
,.
636
aCDa
A
GGN ANCcó
7
3
a
AN
. Trong
A
NG
có
5
cos(AGN)=
65
.Gọi góc
(;)AG CD
thì
5
cos =
65
+TH2: Góc AMD bằng 150
0
. Tính tương tự ta có: thì
13
cos =
75
0.5đ
0.5đ
0.5đ
Đề thi chọn học sinh giỏi môn Toán lớp 11
VnDoc xin giới thiệu tới bạn đọc Đề thi chọn học sinh giỏi lớp 11 môn Toán năm 2018 - 2019 Thị xã Quảng Trị. Nội dung tài liệu gồm 4 câu hỏi bài tập, thời gian làm bài 180 phút, đề thi có đáp án. Mời các bạn tham khảo.
- Bộ đề thi học kì 1 lớp 11 môn Toán năm 2018 - 2019
- Đề thi học kì 1 lớp 11 môn Toán năm 2018 - 2019 Sở GD&ĐT Bắc Giang
- Đề thi học kì 1 lớp 11 môn Toán năm 2018 - 2019 trường THPT Nguyễn Viết Xuân - Vĩnh Phúc
- Đề thi chọn học sinh giỏi lớp 11 môn Toán cấp tỉnh năm 2018 - 2019 Sở GD&ĐT Bắc Ninh
- Đề thi chọn học sinh giỏi lớp 11 môn Toán cấp tỉnh năm 2018 - 2019 Sở GD&ĐT Nghệ An (Bảng A)
- Đề thi chọn học sinh giỏi lớp 11 môn Toán cấp tỉnh năm 2018 - 2019 Sở GD&ĐT Thanh Hóa
- Đề thi chọn học sinh giỏi lớp 11 môn Toán cấp tỉnh năm 2018 - 2019 Sở GD&ĐT Quảng Ngãi
Trên đây VnDoc đã giới thiệu tới các bạn Đề thi chọn học sinh giỏi lớp 11 môn Toán năm 2018 - 2019 trường THPT Thị xã Quảng Trị. Để có kết quả cao hơn trong học tập, VnDoc mời các bạn học sinh tham khảo Giải bài tập Sinh học lớp 11, Giải bài tập Vật lý lớp 11, Giải bài tập Hóa học lớp 11, Giải bài tập Toán lớp 11, Tài liệu học tập lớp 11 mà VnDoc tổng hợp và đăng tải.





