Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Lý thuyết Toán 10 bài 2: Đường thẳng trong mặt phẳng tọa độ CTST

Sách Chân trời sáng tạo

Bài trước

Bài sau

Chúng tôi xin trân trọng giới thiệu bài Lý thuyết Toán lớp 10 bài 2: Đường thẳng trong mặt phẳng tọa độ được VnDoc sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Bài 2: Đường thẳng trong mặt phẳng tọa độ

1. Phương trình đường thẳng
2. Vị trí tương đối của hai đường thẳng
3. Góc giữa hai đường thẳng
4. Khoảng cách từ một điểm đến một đường thẳng
5. Trắc nghiệm Toán 10 bài Đường thẳng trong mặt phẳng tọa độ

1. Phương trình đường thẳng

*Phương trình tham số của đường thẳng

Cho đường thẳng $\Delta$ $\Delta$ đi qua điểm $A\left( {{x_0};{y_0}} \right)$ $A\left( {{x_0};{y_0}} \right)$ và có vectơ chỉ phương $\overrightarrow u \left( {a;b} \right)$ $\overrightarrow u \left( {a;b} \right)$. Khi đó điểm M(x: y) thuộc đường thẳng $\Delta$ $\Delta$ khi và chỉ khi tồn tại số thực t sao cho $\overrightarrow {AM} = t\overrightarrow u$ $\overrightarrow {AM} = t\overrightarrow u$, hay

$\left\{ \begin{array}{l} x = {x_0} + at\\ y = {y_0} + bt \end{array} \right.\;\;\;\;\;\;\;\;$ $\left\{ \begin{array}{l} x = {x_0} + at\\ y = {y_0} + bt \end{array} \right.\;\;\;\;\;\;\;\;$(2)

Hệ (2) được gọi là phương trình tham số của đường thẳng $\Delta$ $\Delta$ (t là tham số).

Ví dụ: Lập phương trình tham số của đường thẳng $\Delta$ $\Delta$ đi qua điểm A(2; -3) và có vectơ chỉ phương $\overrightarrow u \left( {4; - 1} \right)$ $\overrightarrow u \left( {4; - 1} \right)$.

Giải

Phương trình tham số của đường thẳng $\Delta$ $\Delta$ là $\left\{ \begin{array}{l} x = 2 + 4t\\ y = - 3 - t \end{array} \right.$ $\left\{ \begin{array}{l} x = 2 + 4t\\ y = - 3 - t \end{array} \right.$

*Phương trình tổng quát của đường thẳng

Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng ax + by + c =0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax + by + c =0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận $\overrightarrow n \left( {a;b} \right)$ $\overrightarrow n \left( {a;b} \right)$ là một vectơ pháp tuyến.

Ví dụ: Trong mặt phẳng toạ độ, lập phương trình tổng quát của đường thẳng $\Delta$ $\Delta$ đi qua điểm A(2: 1) và nhận $\overrightarrow n \left( {3;4} \right)$ $\overrightarrow n \left( {3;4} \right)$ là một vectơ pháp tuyến.

Giải

Đường thẳng $\Delta$ $\Delta$ có phương trình là 3(x - 2)+ 4(y - 1) = 0 hay 3x + 4y - 10 = 0

Nhận xét: Trong mặt phẳng toạ độ, cho đường thẳng $\Delta$ $\Delta$ : ax + by + c = 0

+ Nếu b = 0 thì phương trình $\Delta$ $\Delta$ có thể đưa về dạng x = m (với $m = - \frac{c}{a}$ $m = - \frac{c}{a}$) và $\Delta$ $\Delta$ vuông góc với Ox.

+ Nếu $b \ne 0$ $b \ne 0$ thì phương trình $\Delta$ $\Delta$ có thể đưa về dạng y = nx + p (với $n = - \frac{a}{b},p = - \frac{c}{b}$ $n = - \frac{a}{b},p = - \frac{c}{b}$)

* Liên hệ giữa đồ thị hàm số bậc nhất và đường thẳng

+ Nếu a=0 và $b \ne 0$ $b \ne 0$ thì phương trình tổng quát ax + by + c =0 trở thành y

Khi đó d là đường thẳng vuông góc với Oy tại điểm $y = - \frac{c}{b}$ $y = - \frac{c}{b}$ (Hình sau).

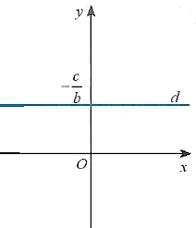
Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ

+ Nếu b =0 và $a \ne 0$ $a \ne 0$ thì phương trình tổng quát ax + by + c =0 trở thành $x = - \frac{c}{a}$ $x = - \frac{c}{a}$

Khí đó d là đường thẳng vuông góc với Ox tại điểm $\left( { - \frac{c}{a};0} \right)$ $\left( { - \frac{c}{a};0} \right)$ (Hình sau)

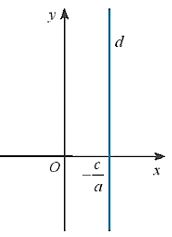
Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ

Trong cả hai trường hợp này, đường thẳng d không phải là đồ thị của hàm số bậc nhất.

2. Vị trí tương đối của hai đường thẳng

Cho ${\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0$ ${\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0$ và ${\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0$ ${\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0$.

Toạ độ giao điểm của ${\Delta _1}$ ${\Delta _1}$ và ${\Delta _2}$ ${\Delta _2}$ là nghiệm của hệ phương trình:

$\left\{ \begin{array}{l} {a_1}x + {b_1}y + {c_1} = 0\\ {a_2}x + {b_2}y + {c_2} = 0 \end{array} \right.$ $\left\{ \begin{array}{l} {a_1}x + {b_1}y + {c_1} = 0\\ {a_2}x + {b_2}y + {c_2} = 0 \end{array} \right.$(*)

${\Delta _1}$ ${\Delta _1}$ cắt ${\Delta _2}$ ${\Delta _2}$ tại $M\left( {{x_0};{y_0}} \right)$ $M\left( {{x_0};{y_0}} \right)$ ⇔ hệ (*) có nghiệm duy nhất $\left( {{x_0};{y_0}} \right)$ $\left( {{x_0};{y_0}} \right)$.

${\Delta _1}$ ${\Delta _1}$ song song với ${\Delta _2}$ ${\Delta _2}$ ⇔ hệ (*) vô nghiệm.

${\Delta _1}$ ${\Delta _1}$ trùng ${\Delta _2}$ ${\Delta _2}$ ⇔ hệ (*) có vô số nghiệm.

Chú ý

Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ

Dựa vào các vectơ chỉ phương $\overrightarrow {{u_1}} ,\overrightarrow {{u_2}}$ $\overrightarrow {{u_1}} ,\overrightarrow {{u_2}}$ hoặc các vectơ pháp tuyến $\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} của \overrightarrow {{\Delta _1}} ,\overrightarrow {{\Delta _2}}$ $\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} của \overrightarrow {{\Delta _1}} ,\overrightarrow {{\Delta _2}}$ ta có:

+ ${{\Delta _1}} Và {{\Delta _2}}$ ${{\Delta _1}} Và {{\Delta _2}}$ song song hoặc trùng nhau ⇔ $\overrightarrow {{u_1}} và \overrightarrow {{u_2}}$ $\overrightarrow {{u_1}} và \overrightarrow {{u_2}}$ cùng phương ⇔ $\overrightarrow {{n_1}} và \overrightarrow {{n_2}}$ $\overrightarrow {{n_1}} và \overrightarrow {{n_2}}$ cùng phương.

+ ${{\Delta _1}} Và {{\Delta _2}}$ ${{\Delta _1}} Và {{\Delta _2}}$ cắt nhau ⇔ $\overrightarrow {{u_1}} và \overrightarrow {{u_2}}$ $\overrightarrow {{u_1}} và \overrightarrow {{u_2}}$ không cùng phương ⇔ $\overrightarrow {{n_1}} và \overrightarrow {{n_2}}$ $\overrightarrow {{n_1}} và \overrightarrow {{n_2}}$ không cùng phương.

Ví dụ: Xét vị trí tương đối giữa đường thẳng $\Delta :x - \sqrt 2 y + 4\sqrt 3 = 0$ $\Delta :x - \sqrt 2 y + 4\sqrt 3 = 0$ và mỗi đường thẳng sau:

$\begin{array}{l} {\Delta _1}:\sqrt 3 x - \sqrt 6 y + 12 = 0;\\ {\Delta _2}:\sqrt 2 x - 2y = 0. \end{array}$ $\begin{array}{l} {\Delta _1}:\sqrt 3 x - \sqrt 6 y + 12 = 0;\\ {\Delta _2}:\sqrt 2 x - 2y = 0. \end{array}$

Giải

Vì $\begin{array}{l} x - \sqrt 2 y + 4\sqrt 3 = 0 \Leftrightarrow \sqrt 3 \left( {x - \sqrt 2 y + 4\sqrt 3 } \right) = 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Leftrightarrow \sqrt 3 x - \sqrt 6 y + 12 = 0. \end{array}$ $\begin{array}{l} x - \sqrt 2 y + 4\sqrt 3 = 0 \Leftrightarrow \sqrt 3 \left( {x - \sqrt 2 y + 4\sqrt 3 } \right) = 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Leftrightarrow \sqrt 3 x - \sqrt 6 y + 12 = 0. \end{array}$

Vậy ${{\Delta}} và {{\Delta _1}}$ ${{\Delta}} và {{\Delta _1}}$ là một, tức là chúng trùng nhau.

Hai đường thẳng ${{\Delta}} và {{\Delta _2}}$ ${{\Delta}} và {{\Delta _2}}$ có hai vectơ pháp tuyến $\overrightarrow n \left( {1; - \sqrt 2 } \right) và \overrightarrow {{n_2}} \left( {\sqrt 2 ; - 2} \right)$ $\overrightarrow n \left( {1; - \sqrt 2 } \right) và \overrightarrow {{n_2}} \left( {\sqrt 2 ; - 2} \right)$ cùng phương.

Do đó, chúng song song hoặc trùng nhau. Mặt khác, điểm O(0; 0) thuộc đường thẳng ${{\Delta _2}}$ ${{\Delta _2}}$ nhưng không thuộc đường thẳng ${{\Delta}}$ ${{\Delta}}$ nên hai đường thẳng này không trùng nhau.

Vậy ${{\Delta}} và {{\Delta _2}}$ ${{\Delta}} và {{\Delta _2}}$ song song với nhau.

3. Góc giữa hai đường thẳng

- Hai đường thẳng cắt nhau tạo thành bốn góc, số đo của góc không tù được gọi là số đo góc (hay đơn giản là góc) giữa hai đường thẳng.

- Góc giữa hai đường thẳng song song hoặc trùng nhau được quy ước bằng 0°.

- Cho hai đường thẳng

${\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0$ ${\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0$ và ${\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0$ ${\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0$.

Với các vectơ pháp tuyến $\overrightarrow {{n_1}} \left( {{a_1};{b_1}} \right) và \overrightarrow {{n_2}} \left( {{a_2};{b_2}} \right)$ $\overrightarrow {{n_1}} \left( {{a_1};{b_1}} \right) và \overrightarrow {{n_2}} \left( {{a_2};{b_2}} \right)$ trong ứng. Khi đó, góc $\varphi$ $\varphi$ giữa hai đường thẳng đó được xác định thông qua công thức

$cos\varphi = \left| {cos\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} .\sqrt {{a_2}^2 + {b_2}^2} }}$ $cos\varphi = \left| {cos\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} .\sqrt {{a_2}^2 + {b_2}^2} }}$

Ví dụ: Tính góc giữa hai đường thẳng

${\Delta _1}:\sqrt 3 x - y + 2 = 0 và {\Delta _2}:x - \sqrt 3 y - 2 = 0.$ ${\Delta _1}:\sqrt 3 x - y + 2 = 0 và {\Delta _2}:x - \sqrt 3 y - 2 = 0.$

Giải

Vectơ pháp tuyến của ${{\Delta _1}}$ ${{\Delta _1}}$ là $\overrightarrow {{n_1}} = \left( {\sqrt 3 ; - 1} \right)$ $\overrightarrow {{n_1}} = \left( {\sqrt 3 ; - 1} \right)$, của ${{\Delta _2}}$ ${{\Delta _2}}$ là $\overrightarrow {{n_2}} = \left( {1; - \sqrt 3 } \right)$ $\overrightarrow {{n_2}} = \left( {1; - \sqrt 3 } \right)$.

Gọi \varphi là góc giữa hai đường thẳng ${{\Delta _1}}$ ${{\Delta _1}}$ và ${{\Delta _2}}$ ${{\Delta _2}}$. Ta có

$cos\varphi = \left| {cos\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {\sqrt 3 .1 + \left( { - 1} \right).\left( { - \sqrt 3 } \right)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - \sqrt 3 } \right)}^2}} }} = \frac{{\sqrt 3 }}{2}.$ $cos\varphi = \left| {cos\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {\sqrt 3 .1 + \left( { - 1} \right).\left( { - \sqrt 3 } \right)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - \sqrt 3 } \right)}^2}} }} = \frac{{\sqrt 3 }}{2}.$

Do đó, góc giữa ${{\Delta _1}}$ ${{\Delta _1}}$ và ${{\Delta _2}}$ ${{\Delta _2}}$ là $\varphi = {30^0}$ $\varphi = {30^0}$.

4. Khoảng cách từ một điểm đến một đường thẳng

Cho điểm $M\left( {{x_0};{y_0}} \right)$ $M\left( {{x_0};{y_0}} \right)$ và đường thẳng $\Delta :ax + by + c = 0$ $\Delta :ax + by + c = 0$. Khoảng cách từ điểm M đến đường thẳng $\Delta$ $\Delta$ , kí hiệu là $d\left( {M,\Delta } \right)$ $d\left( {M,\Delta } \right)$, được tính bởi công thức

$d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$ $d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$

Ví dụ: Tính khoảng cách từ điểm M(2; 4) đến đường thẳng $\Delta$ $\Delta$ :3x + 4y - 12 = 0.

Giải

Áp dụng công thức tính khoảng cách từ điểm M đến đường thẳng $\Delta$ $\Delta$, ta có

$d\left( {M,\Delta } \right) = \frac{{\left| {3.2 + 4.4 - 12} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{10}}{5} = 2$ $d\left( {M,\Delta } \right) = \frac{{\left| {3.2 + 4.4 - 12} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{10}}{5} = 2$

Vậy khoảng cách từ điểm M đến đường thẳng $\Delta$ $\Delta$ là 2.