Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Lý thuyết Toán 10 bài 4: Tích vô hướng của hai vectơ CTST

Sách Chân trời sáng tạo

Bài trước

Bài sau

Lý thuyết Toán lớp 10 bài 4: Tích vô hướng của hai vectơ được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

A. Lý thuyết Toán 10 bài 4

1. Góc giữa hai vectơ

Cho hai vecto $\overrightarrow u$ $\overrightarrow u$và $\overrightarrow v$ $\overrightarrow v$ khác $\overrightarrow 0$ $\overrightarrow 0$. Góc giữa hai vecto $\overrightarrow u$ $\overrightarrow u$ và $\overrightarrow v$ $\overrightarrow v$, kí hiệu $\left( {\;\overrightarrow u ,\overrightarrow v } \right)$ $\left( {\;\overrightarrow u ,\overrightarrow v } \right)$

*Cách xác định góc

Chọn điểm A bất kì, vẽ $\overrightarrow {AB} = \overrightarrow u, \overrightarrow {AC} = \overrightarrow v$ $\overrightarrow {AB} = \overrightarrow u, \overrightarrow {AC} = \overrightarrow v$. Khi đó $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}$ $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}$

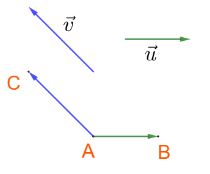
* Các trường hợp đặc biệt:

+) $\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha$ $\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha$ tùy ý, với ${0^ \circ } \le \alpha \le {180^ \circ }$ ${0^ \circ } \le \alpha \le {180^ \circ }$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v$ $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v$ hoặc $\overrightarrow v \bot \overrightarrow u$ $\overrightarrow v \bot \overrightarrow u$. Đặc biệt: $\overrightarrow 0 \bot \overrightarrow u \;\;\forall \overrightarrow u \;$ $\overrightarrow 0 \bot \overrightarrow u \;\;\forall \overrightarrow u \;$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$cùng hướng

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ ngược hướng

Chú ý:

- Từ định nghĩa ta có $\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right)$ $\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right)$

- Góc giữa hai vectơ cùng hướng và khác ${\overrightarrow 0 }$ ${\overrightarrow 0 }$ luôn bằng 0^o

- Góc giữa hai vectơ ngược hướng và khác ${\overrightarrow 0 }$ ${\overrightarrow 0 }$ luôn bằng 180^o,

- Trong trường hợp có ít nhất một trong hai vectơ ${\overrightarrow a }$ ${\overrightarrow a }$ hoặc ${\overrightarrow b }$ ${\overrightarrow b }$ là vectơ ${\overrightarrow 0 }$ ${\overrightarrow 0 }$ thì ta quy ước

số đo góc giữa hai vectơ đó là tuỷ ý (từ 0^o đến 180^o)

Ví dụ: Cho hình vuông ABCD có tâm I là giao điểm của hai đường chéo. Tìm các góc

$\begin{array}{l} a)\left( {\overrightarrow {IB} ,\overrightarrow {AB} } \right)\\ b)\left( {\overrightarrow {IB} ,\overrightarrow {AI} } \right)\\ c)\left( {\overrightarrow {IB} ,\overrightarrow {DB} } \right)\\ d)\left( {\overrightarrow {IA} ,\overrightarrow {IC} } \right) \end{array}$ $\begin{array}{l} a)\left( {\overrightarrow {IB} ,\overrightarrow {AB} } \right)\\ b)\left( {\overrightarrow {IB} ,\overrightarrow {AI} } \right)\\ c)\left( {\overrightarrow {IB} ,\overrightarrow {DB} } \right)\\ d)\left( {\overrightarrow {IA} ,\overrightarrow {IC} } \right) \end{array}$

Giải

a) Ta có: $\overrightarrow {DI} = \overrightarrow {IB} ,\overrightarrow {DC} = \overrightarrow {AB}$ $\overrightarrow {DI} = \overrightarrow {IB} ,\overrightarrow {DC} = \overrightarrow {AB}$, suy ra $\left( {\overrightarrow {IB} ,\overrightarrow {AB} } \right) = \left( {\overrightarrow {DI} ,\overrightarrow {DC} } \right) = \widehat {IDC} = {45^o}$ $\left( {\overrightarrow {IB} ,\overrightarrow {AB} } \right) = \left( {\overrightarrow {DI} ,\overrightarrow {DC} } \right) = \widehat {IDC} = {45^o}$

b) Ta có: $\overrightarrow {IC} = \overrightarrow {AI}$ $\overrightarrow {IC} = \overrightarrow {AI}$, suy ra $\left( {\overrightarrow {IB} ,\overrightarrow {AI} } \right) = \left( {\overrightarrow {IB} ,\overrightarrow {IC} } \right) = \widehat {BIC} = {90^o}$ $\left( {\overrightarrow {IB} ,\overrightarrow {AI} } \right) = \left( {\overrightarrow {IB} ,\overrightarrow {IC} } \right) = \widehat {BIC} = {90^o}$

c) Do hai vecto $\overrightarrow {IB} ,\overrightarrow {DB}$ $\overrightarrow {IB} ,\overrightarrow {DB}$ cùng hướng nên ta có $\left( {\overrightarrow {IB} ,\overrightarrow {DB} } \right) = {0^o}$ $\left( {\overrightarrow {IB} ,\overrightarrow {DB} } \right) = {0^o}$

d) Do hai vecto ${\overrightarrow {IA} ,\overrightarrow {IC} }$ ${\overrightarrow {IA} ,\overrightarrow {IC} }$ ngược hướng nên ta có $\left( {\overrightarrow {IA} ,\overrightarrow {IC} } \right) = {180^o}$ $\left( {\overrightarrow {IA} ,\overrightarrow {IC} } \right) = {180^o}$

2. Tích vô hướng của hai vectơ

Tích vô hướng của hai vecto $\overrightarrow u ,\;\overrightarrow v : \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)$ $\overrightarrow u ,\;\overrightarrow v : \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)$

Chú ý:

+) $\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u \bot \;\overrightarrow v \;\;$ $\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u \bot \;\overrightarrow v \;\;$

+) $\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}$ $\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}$

Ví dụ: Cho tam giác đều ABC cỏ cạnh bằng 4 và có đường cao AH. Tính các tích vô hướng:

$\begin{array}{l} a){\rm{ }}\overrightarrow {AB} .\overrightarrow {AC} ;\\ b){\rm{ }}\overrightarrow {AB} .\overrightarrow {BC} ;\\ c){\rm{ }}\overrightarrow {AH} .\overrightarrow {BC} \end{array}$ $\begin{array}{l} a){\rm{ }}\overrightarrow {AB} .\overrightarrow {AC} ;\\ b){\rm{ }}\overrightarrow {AB} .\overrightarrow {BC} ;\\ c){\rm{ }}\overrightarrow {AH} .\overrightarrow {BC} \end{array}$

Giải

$\begin{array}{l} a){\rm{ }}\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.cos\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = 4.4.cos{60^0} = 16.\frac{1}{2} = 8\\ b){\rm{ }}\overrightarrow {AB} .\overrightarrow {BC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.cos\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = 4.4.cos{120^0} = 16.\left( { - \frac{1}{2}} \right) = - 8\\ c){\rm{ }}\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.cos\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.cos{90^0} = 0 \end{array}$ $\begin{array}{l} a){\rm{ }}\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.cos\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = 4.4.cos{60^0} = 16.\frac{1}{2} = 8\\ b){\rm{ }}\overrightarrow {AB} .\overrightarrow {BC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.cos\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = 4.4.cos{120^0} = 16.\left( { - \frac{1}{2}} \right) = - 8\\ c){\rm{ }}\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.cos\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.cos{90^0} = 0 \end{array}$

3. Tính chất của tích vô hướng

Cho 3 vecto \ $\overrightarrow u ,\overrightarrow v ,\overrightarrow w$ $\overrightarrow u ,\overrightarrow v ,\overrightarrow w$ bất kì và mọi số thực k, ta có:

$\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}$ $\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}$

Nhận xét

$\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}$ $\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}$

Ví dụ: Cho tam giác ABC. TÍnh cạnh AB theo hai cạnh còn lại và góc C

Giải

Ta có:

$A{B^2} = {\overrightarrow {AB} ^2} = {\left( {\overrightarrow {CB} - \overrightarrow {CA} } \right)^2} = {\overrightarrow {CB} ^2} + {\overrightarrow {CA} ^2} - 2\overrightarrow {CB} .\overrightarrow {CA} = {\overrightarrow {CB} ^2} + {\overrightarrow {CA} ^2} - 2CB.CA.\cos C$ $A{B^2} = {\overrightarrow {AB} ^2} = {\left( {\overrightarrow {CB} - \overrightarrow {CA} } \right)^2} = {\overrightarrow {CB} ^2} + {\overrightarrow {CA} ^2} - 2\overrightarrow {CB} .\overrightarrow {CA} = {\overrightarrow {CB} ^2} + {\overrightarrow {CA} ^2} - 2CB.CA.\cos C$

hay ${c^2} = {a^2} + {b^2} - 2.b.c.\cos C$ ${c^2} = {a^2} + {b^2} - 2.b.c.\cos C$

B. Bài tập minh họa

Câu 1: Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng $\sqrt 2$ $\sqrt 2$

Tính các tích vô hướng: $\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {BC} ,\overrightarrow {BA} .\overrightarrow {BC}$ $\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {BC} ,\overrightarrow {BA} .\overrightarrow {BC}$

Hướng dẫn giải

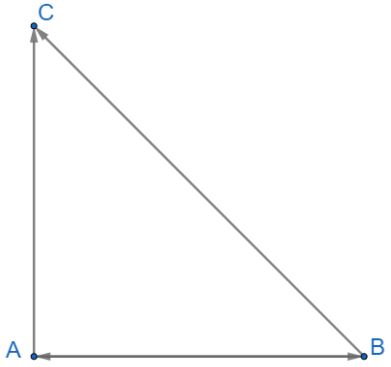
+) Ta có: $AB \bot AC \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0$ $AB \bot AC \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0$

+) $\overrightarrow {AC} .\overrightarrow {BC} = \left| {\overrightarrow {AC} } \right|.\left| {\overline {BC} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right)$ $\overrightarrow {AC} .\overrightarrow {BC} = \left| {\overrightarrow {AC} } \right|.\left| {\overline {BC} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right)$

Ta có: $BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \Leftrightarrow \sqrt {2A{C^2}} = \sqrt 2 \Rightarrow AC = 1$ $BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \Leftrightarrow \sqrt {2A{C^2}} = \sqrt 2 \Rightarrow AC = 1$

$\\Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1$ $\\Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1$

+) $\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1$ $\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1$

Câu 2: Hai vectơ $\overrightarrow a ,\overrightarrow b$ $\overrightarrow a ,\overrightarrow b$có độ dài lần lượt là 3 và 8 có tích vô hướng là $12\sqrt 2$ $12\sqrt 2$.Tính góc giữa hai vectơ $\overrightarrow a,\overrightarrow b$ $\overrightarrow a,\overrightarrow b$

Hướng dẫn giải

Ta có: $\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)$ $\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)$

$\\Leftrightarrow 12\sqrt 2 = 3.8.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}$ $\\Leftrightarrow 12\sqrt 2 = 3.8.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}$

$\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ$ $\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ$

Vậy góc giữa hai vectơ $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ là $45^\circ$ $45^\circ$