Lý thuyết Toán 10 bài 2: Hoán vị, chỉnh hợp và tổ hợp CTST

Kí hiệu P_n là số hoán vị của n phần tử

Người ta chứng minh được rằng:

Số các hoán vị của m phần tử (n ≥ 1) bằng

\({P_n} = n\left( {n - 1} \right)\left( {n - 2} \right)...2.1.\)

Chú ý:

+ Ta đưa vào kí hiệu: \(n! = n\left( {n - 1} \right)\left( {n - 2} \right)...2.1.\) và đọc là n giai thừa hoặc giai thừa của n.

Khi đó, P_n = n!.

+ Quy ước: 0! =1.

Ví dụ 

Bãi đỗ xe ô tô còn lại ba chỗ trông như Hình bên dưới.

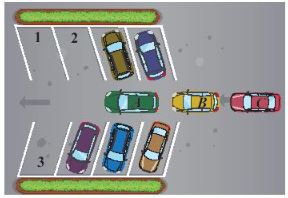
Có ba chiếc ö tô đkí hiệu A, B, C) đang đi vào bãi để đỗ xe.

a) Có bao nhiêu cách sắp xếp ba chiếc xe vào ba chỗ trông?

b) Vẽ sơ đồ hình cây về các cách sắp xếp và kiểm tra kết quả tính toán ở trên.

Giải

a) Mỗi cách sắp xếp ba chiếc xe vào ba chỗ trống là một hoán vị của ba chiếc xe. Do đó, số cách sắp xếp ba chiếc xe vào ba chỗ trồng là P₃ = 3.2.1= 6 (cách)

b) Sơ đồ hình cây như Hình bên dưới.

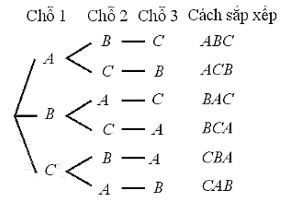
Sơ đồ có ba cành lớn, mỗi cành lớn có hai cành vừa, mỗi cành vừa có một cành bé. Tử đó, số cành bẻ bằng 3.2. 1 =6. Từ đó, số cách sắp xếp ba chiếc xe vào ba chỗ trông là 6 cách.

Người ta chứng minh được rằng

Số các chỉnh hợp chập k của n phần tử 1 ≤ k ≤ n bằng

\(A_n^k = n\left( {n - 1} \right)\left( {n - 2} \right)...\left( {n - k + 1} \right) = \frac{{n!}}{{\left( {n - k} \right)!}}\)

Nhận xét: Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó.

Ta có: \({P_n} = A_n^k,n \ge 1.\)

Ví dụ: 

Phần thi chung kết nội dung chạy cư li 1 500 m của một giải đấu có 10 vận động viên tham gia. Có bao nhiêu khả năng về kết quả 3 vận động viên đoạt huy chương vàng, bạc và đồng sau khi phần thi kết thúc? Biết rằng không có hai vận động viên nào về đích cùng lúc?

Giải

Mỗi kết quả về 3 vận động viên đoạt huy chương vàng, bạc và đồng của nội dung thi đấu là một chỉnh hợp chập 3 của 10 vận động viên.

Do đó, số kết quả có thể là \(A_{10}^3 = 10.9.8 = 720\).

Kí hiệu \(C_n^k\) là số tổ hợp chập k của n phần tử \(1 \le k \le n\)

Người ta chứng minh được rằng:

Số các tổ hợp chập k của n phần tử \\(1 \le k \le n\) bằng

\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\)

Chú ý: Người ta quy ước \(C_n^0 = 1\) 

Ví dụ 

Tổ Một có 9 thành viên. Tuần tới là phiên trực nhật của tổ, nên cần phân công 4 bạn đi bê ghế của lớp cho buổi chào cờ

a) Tổ có bao nhiêu cách phân công 4 bạn đi bê ghế?

b) Tổ có bao nhiêu cách chọn 5 bạn không phải đi bê ghế?

Giải

a) Mỗi cách phân công 4 bạn từ 9 bạn là một tổ hợp chập 4 của 9 bạn. Do đó, số cách phân công 4 bạn của tổ đi bê ghế là

\(C_9^4 = \frac{{9!}}{{4!5!}} = \frac{{9.8.7.6}}{{4.3.2}} = 126\) (cách)

b) Tương tự, số cách chọn 5 bạn từ 9 bạn không phải đi bê ghế là

\(C_9^5 = \frac{{9!}}{{5!4!}} = 126 (cách)\)

Nhận xét: Ở ví dụ trên, ta thấy \(C_9^4 = C_9^5\). Tổng quát, ta có hệ thức:

\(C_n^k = C_n^{n - k}\left( {0 \le k \le n} \right)\)

Với một số máy tính cầm tay, ta có thể tính toán nhanh số các hoán vị, chỉnh hợp và tổ hợp.

Ví dụ

a) Đề tính \({P_8} = 8!\), ta ấn liên tiếp các phím  thì nhận được kết quả là 40 320.

b) Để tính \(A_{12}^5\), ta ấn liên tiếp các phím thì nhận được kết quả là 95040.

c) Để tính \(C_{20}^{11}\), ta ấn liên tiếp các phím 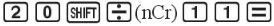thì nhận được kết quả là 167 960.

Câu 1: Một giải bóng đá có 14 đội bóng tham gia. Có bao nhiêu khả năng về thứ hạng các đội bóng khi mùa giải kết thúc?

Hướng dẫn giải

Mỗi khả năng về thứ hạng của các đội bóng trong mùa giải là hoán vị của các đội bóng tham gia. Do đó, số khả năng về thứ hạng của các đội bóng trong mùa giải là:\({P_{14}} = 14!\) (cách)

Câu 2: Từ 7 chữ số số 1; 2; 3; 4; 5; 6; 7 lập được các số có 3 chữ số đôi một khác nhau

a) Có thể lập được bao nhiêu số như vậy?

b) Trong các số đó có bao nhiêu số lẻ?

Hướng dẫn giải

a) Mỗi số có 3 chữ số đôi một khác nhau lập được từ 7 chữ số đã cho là một chỉnh hợp chập 3 của 7 chữ số. Do đó, số các số lập được là

\(A_7^3 = 7.6.5 = 210\) (số)

b) Việc lập ra được một số lẻ phải qua 2 công đoạn

Công đoạn 1: Chọn chữ số hàng đơn vị là chữ số lẻ, có 4 cách chọn (1; 3; 5 hoặc 7)

Công đoạn 2: Chọn 2 chữ số bất kì trong 6 chữ số còn lại và sắp xếp chúng cho vị trí chữ số hàng trăm và hàng chục, mỗi số như vậy là một chỉnh hợp chập 2 của 6 phần tử, nên số các số được lập ra là:

\(A_6^2 = 6.5 = 30\) (cách)

Áp dụng quy tắc nhân, ta có số các số có 3 chữ số lập được từ 7 chữ số đã cho là số lẻ là:

\(4.30 = 120\) (số)

Câu 3: Tính:

a) \(C_7^2\)

b)  \(C_9^0 + C_9^9\)

c) \(C_{15}^3 - C_{14}^3\)

Hướng dẫn giải

a) \(C_7^2 = \frac{{7!}}{{2!.5!}} = \frac{{7.6}}{2} = 21\)

b) \(C_9^0 + C_9^9 = \frac{{9!}}{{0!.9!}} + \frac{{9!}}{{9!.0!}} = 2\)

c) \(C_{15}^3 - C_{14}^3 = \frac{{15!}}{{3!.12!}} - \frac{{14!}}{{3!.11!}} = \frac{{15.14.13}}{{3.2.1}} - \frac{{14.13.12}}{{3.2.1}} = 91\)

C. Trắc nghiệm Toán 10 bài 2