VnDoc.com

Lý thuyết Toán 10 bài 1: Tọa độ của vectơ CTST

Sách Chân trời sáng tạo

Bài trước

Bài sau

Lý thuyết Toán lớp 10 bài 1: Tọa độ của vectơ được VnDoc sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Bài 1: Tọa độ của vectơ

1. Toạ độ của vectơ đối với một hệ trục tọa độ
2. Biểu thức toạ độ của các phép toán vectơ
3. Áp dụng của tọa độ vectơ
4. Trắc nghiệm Toán 10 bài 1

1. Toạ độ của vectơ đối với một hệ trục tọa độ

Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy được gọi là mặt phẳng tọa độ Oxy, hay gọi tắt là mặt phẳng Oxy.

*Toạ độ của một vectơ

Trong mặt phẳng Oxy, cặp số (x; y) trong biểu diễn $\overrightarrow a = x\overrightarrow i + y\overrightarrow j$ $\overrightarrow a = x\overrightarrow i + y\overrightarrow j$ được gọi là tọa độ của vectơ $\overrightarrow a$ $\overrightarrow a$ kí hiệu $\overrightarrow a$ $\overrightarrow a$ = (x, y), x gọi là hoành độ, y gọi là tung độ của vectơ $\overrightarrow a$ $\overrightarrow a$.

Chú ý:

+ $\overrightarrow a = \left( {x,y} \right) \Leftrightarrow \overrightarrow a = x\overrightarrow i + y\overrightarrow j$ $\overrightarrow a = \left( {x,y} \right) \Leftrightarrow \overrightarrow a = x\overrightarrow i + y\overrightarrow j$

+ Nếu cho $\overrightarrow a = \left( {x,y} \right) và \overrightarrow b = \left( {x$ $\overrightarrow a = \left( {x,y} \right) và \overrightarrow b = \left( {x',y'} \right)$ thì $\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l} x = x$ $\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l} x = x'\\ y = y' \end{array} \right.$

*Tọa độ của một điểm

Trong mặt phẳng tọa độ, cho một điểm M tùy ý. Tọa độ của vectơ $\overrightarrow {OM}$ $\overrightarrow {OM}$ được gọi là tọa độ của điểm M.

Nhận xét:

+ Nếu $\overrightarrow {OM} = \left( {x;y} \right)$ $\overrightarrow {OM} = \left( {x;y} \right)$ thì cặp số (x; y) là tọa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M

+ $M\left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j$ $M\left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j$

Chú ý: Hoành độ của điểm M còn được kí hiệu là x_M, tung độ của điểm M còn được kí hiệu là y_M. Khi đó ta viết M(x_M; y_M).

Ví dụ:

Trong mặt phẳng Oxy, cho ba điểm A, B, C được biểu diễn như Hình sau.

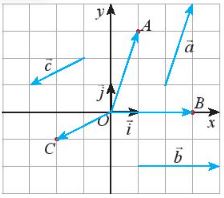
Toán 10 Bài 1: Tọa độ của vectơ

a) Hãy biểu thị các vectơ $\overrightarrow {OA} ,\overrightarrow {OB} ,\overrightarrow {OC}$ $\overrightarrow {OA} ,\overrightarrow {OB} ,\overrightarrow {OC}$ qua hai vectơ $\overrightarrow i và \overrightarrow j$ $\overrightarrow i và \overrightarrow j$ .

b) Tìm toa độ của các vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$và các điểm A, B, C.

Giải

a) Ta có: $\overrightarrow {OA} = \overrightarrow i + 3\overrightarrow j ,\overrightarrow {OB} = 3\overrightarrow i + 0\overrightarrow j ,\overrightarrow {OC} = - 2\overrightarrow i - \overrightarrow j$ $\overrightarrow {OA} = \overrightarrow i + 3\overrightarrow j ,\overrightarrow {OB} = 3\overrightarrow i + 0\overrightarrow j ,\overrightarrow {OC} = - 2\overrightarrow i - \overrightarrow j$

b) Từ kết quả trên, suy ra: $\overrightarrow a = \overrightarrow {OA} = (1;3),\overrightarrow b = \overrightarrow {OB} = (3;0),\overrightarrow c = \overrightarrow {OC} = ( - 2; - 1)$ $\overrightarrow a = \overrightarrow {OA} = (1;3),\overrightarrow b = \overrightarrow {OB} = (3;0),\overrightarrow c = \overrightarrow {OC} = ( - 2; - 1)$

Do đó A(1; 3), B(3: 0), C(-2; -1)

2. Biểu thức toạ độ của các phép toán vectơ

Cho hai vectơ $\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right)$ $\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right)$ và số thực k. Khi đó:

$\begin{array}{l} 1)\;\;\;\overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right);\\ 2)\;\;\;\overrightarrow a - \overrightarrow b = \left( {{a_1} - {b_1};{a_2} - {b_2}} \right);\\ 3)\;\;\;k\overrightarrow a = \left( {k{a_1};k{a_2}} \right);\\ 4)\;\;\;\overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2}. \end{array}$ $\begin{array}{l} 1)\;\;\;\overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right);\\ 2)\;\;\;\overrightarrow a - \overrightarrow b = \left( {{a_1} - {b_1};{a_2} - {b_2}} \right);\\ 3)\;\;\;k\overrightarrow a = \left( {k{a_1};k{a_2}} \right);\\ 4)\;\;\;\overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2}. \end{array}$

Ví dụ: Cho hai vectơ $\overrightarrow a = \left( {1;5} \right),\overrightarrow b = \left( {4; - 2} \right)$ $\overrightarrow a = \left( {1;5} \right),\overrightarrow b = \left( {4; - 2} \right)$. Tìm tọa độ của các vectơ $\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,3\overrightarrow a , - 5\overrightarrow b$ $\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,3\overrightarrow a , - 5\overrightarrow b$

Giải

$\begin{array}{l} \overrightarrow a + \overrightarrow b = \left( {1 + 4;5 + \left( { - 2} \right)} \right) = \left( {5;3} \right);\\ \overrightarrow a - \overrightarrow b = \left( {1 - 4;5 - \left( { - 2} \right)} \right) = \left( { - 3;7} \right);\\ 3\overrightarrow a = \left( {3.1;3.5} \right) = \left( {3;15} \right);\\ - 5.\overrightarrow b = \left( { - 5.4; - 5.\left( { - 2} \right)} \right) = \left( { - 20;10} \right) \end{array}$ $\begin{array}{l} \overrightarrow a + \overrightarrow b = \left( {1 + 4;5 + \left( { - 2} \right)} \right) = \left( {5;3} \right);\\ \overrightarrow a - \overrightarrow b = \left( {1 - 4;5 - \left( { - 2} \right)} \right) = \left( { - 3;7} \right);\\ 3\overrightarrow a = \left( {3.1;3.5} \right) = \left( {3;15} \right);\\ - 5.\overrightarrow b = \left( { - 5.4; - 5.\left( { - 2} \right)} \right) = \left( { - 20;10} \right) \end{array}$

3. Áp dụng của tọa độ vectơ

* Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng

Cho hai điểm $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$ $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$. Ta có:

$\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)$ $\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)$

* Toạ độ trung điểm của đoạn thẳng và trọng tâm của tam giác

Cho hai điểm $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$ $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$. Tọa độ trung điểm $M\left( {{x_M};{y_M}} \right)$ $M\left( {{x_M};{y_M}} \right)$ của đoạn thẳng AB là

${x_M} = \frac{{{x_A} + {x_B}}}{2};{y_M} = \frac{{{y_A} + {y_B}}}{2}$ ${x_M} = \frac{{{x_A} + {x_B}}}{2};{y_M} = \frac{{{y_A} + {y_B}}}{2}$

Cho tam giác ABC có $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)$ $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)$. Tọa độ trọng tâm $G\left( {{x_G};{y_G}} \right)$ $G\left( {{x_G};{y_G}} \right)$ của tam giác ABC là:

${x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}$ ${x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}$

Ví dụ

Cho tam giác MNP có tọa độ các đỉnh là M(2; 2), N(6; 3) và P(5; 5)

a) Tìm tọa đô trung điểm E của cạnh MN.

b) Tìm tọa độ trọng tâm G của tam giác MNP.

Giải

Ta có: ${x_E} = \frac{{{x_M} + {x_N}}}{2} = \frac{{2 + 6}}{2} = 4;{y_E} = \frac{{{y_M} + {y_N}}}{2} = \frac{{2 + 3}}{2} = \frac{5}{2}. Vậy E\left( {4;\frac{5}{2}} \right)$ ${x_E} = \frac{{{x_M} + {x_N}}}{2} = \frac{{2 + 6}}{2} = 4;{y_E} = \frac{{{y_M} + {y_N}}}{2} = \frac{{2 + 3}}{2} = \frac{5}{2}. Vậy E\left( {4;\frac{5}{2}} \right)$

Ta có: ${x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 6 + 5}}{3} = \frac{{13}}{3};{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{2 + 3 + 5}}{3} = \frac{{10}}{3}$ ${x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 6 + 5}}{3} = \frac{{13}}{3};{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{2 + 3 + 5}}{3} = \frac{{10}}{3}$

Vậy $G\left( {\frac{{13}}{3};\frac{{10}}{3}} \right)$ $G\left( {\frac{{13}}{3};\frac{{10}}{3}} \right)$