Lý thuyết Toán 10 bài 3: Nhị thức Newton CTST

Sách Chân trời sáng tạo

Chúng tôi xin trân trọng giới thiệu bài Lý thuyết Toán lớp 10 bài 3: Nhị thức Newton được VnDoc sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

A. Lý thuyết Toán 10 bài 3

Ta có hai công thức khai triển sau:

$\begin{array}{l} \begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}.} \end{array}\\ \begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.} \end{array} \end{array}$ $\begin{array}{l} \begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}.} \end{array}\\ \begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.} \end{array} \end{array}$

Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) ${\left( {a + b} \right)^n}$ ${\left( {a + b} \right)^n}$ ứng với n = 4 và n = 5.

Chú ý:

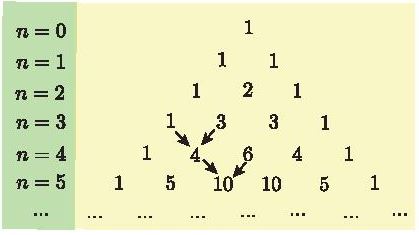
Các hệ số trong khai triển nhị thức Newton ${\left( {a + b} \right)^n}$ ${\left( {a + b} \right)^n}$ với n =0; 1; 2; 3;.. được viết thành từng hàng và xếp thành bảng số như bên. Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của hai số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).

Bảng số trên được gọi là tam giác Pasca (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 — 1662).

Ví dụ

Sử dụng công thức nhị thức Newton, hãy khai

$\begin{array}{l} a){\left( {x + 3} \right)^4}\\ b){\left( {1 - x} \right)^5} \end{array}$ $\begin{array}{l} a){\left( {x + 3} \right)^4}\\ b){\left( {1 - x} \right)^5} \end{array}$

Giải

a) Theo công thức nhị thức Newton, ta có

$\begin{array}{l} {\left( {x + 3} \right)^4} = 1.{x^4} + 4.{x^3}.3 + 6.{x^2}{.3^2} + 4.x{.3^3} + {1.3^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {x^4} + 4.3.{x^3} + 6.9.{x^2} + 4.27.x + 81\\ \;\;\;\;\;\;\;\;\;\;\;\; = {x^4} + 12.{x^3} + 54{x^2} + 108.x + 81 \end{array}$ $\begin{array}{l} {\left( {x + 3} \right)^4} = 1.{x^4} + 4.{x^3}.3 + 6.{x^2}{.3^2} + 4.x{.3^3} + {1.3^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {x^4} + 4.3.{x^3} + 6.9.{x^2} + 4.27.x + 81\\ \;\;\;\;\;\;\;\;\;\;\;\; = {x^4} + 12.{x^3} + 54{x^2} + 108.x + 81 \end{array}$

b) Theo công thức nhị thức Newton, ta có:

$\begin{array}{l} {\left( {1 - x} \right)^5} = 1 + 5.\left( { - x} \right) + 10.{\left( { - x} \right)^2} + 10.{\left( { - x} \right)^3} + 5.{\left( { - x} \right)^4} + 1{\left( { - x} \right)^5}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = 1 - 5x + 10{x^2} - 10{x^3} + 5{x^4} - {x^5} \end{array}$ $\begin{array}{l} {\left( {1 - x} \right)^5} = 1 + 5.\left( { - x} \right) + 10.{\left( { - x} \right)^2} + 10.{\left( { - x} \right)^3} + 5.{\left( { - x} \right)^4} + 1{\left( { - x} \right)^5}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = 1 - 5x + 10{x^2} - 10{x^3} + 5{x^4} - {x^5} \end{array}$

B. Bài tập minh họa

Câu 1: Khai triển các biểu thức sau

a) ${\left( {x - 2} \right)^4}$ ${\left( {x - 2} \right)^4}$

b) ${\left( {x + 2y} \right)^5}$ ${\left( {x + 2y} \right)^5}$

Hướng dẫn giải

a) ${\left( {x -2} \right)^4}$ ${\left( {x -2} \right)^4}$

$\begin{array}{l} = {x^4} + 4{x^3}.\left( { - 2} \right) + 6{x^2}.{\left( { - 2} \right)^2} + 4x{\left( { - 2} \right)^3} + {\left( { - 2} \right)^4}\\ = {x^4} - 8{x^3} + 24{x^2} - 32x + 16\end{array}$ $\begin{array}{l} = {x^4} + 4{x^3}.\left( { - 2} \right) + 6{x^2}.{\left( { - 2} \right)^2} + 4x{\left( { - 2} \right)^3} + {\left( { - 2} \right)^4}\\ = {x^4} - 8{x^3} + 24{x^2} - 32x + 16\end{array}$

b) ${\left( {x + 2y} \right)^5}$ ${\left( {x + 2y} \right)^5}$

$\begin{array}{l} = {x^5} + 5.{x^4}.\left( {2y} \right) + 10.{x^3}.{\left( {2y} \right)^2} + 10.{x^2}.{\left( {2y} \right)^3} + 5.x.{\left( {2y} \right)^4} + 1.{\left( {2y} \right)^5}\\ = {x^5} + 10{x^4}y + 40{x^3}{y^3} + 80{x^2}{y^3} + 80x{y^4} + 32{y^5}\end{array}$ $\begin{array}{l} = {x^5} + 5.{x^4}.\left( {2y} \right) + 10.{x^3}.{\left( {2y} \right)^2} + 10.{x^2}.{\left( {2y} \right)^3} + 5.x.{\left( {2y} \right)^4} + 1.{\left( {2y} \right)^5}\\ = {x^5} + 10{x^4}y + 40{x^3}{y^3} + 80{x^2}{y^3} + 80x{y^4} + 32{y^5}\end{array}$

Câu 2: Sử dụng công thức nhị thức Newton, chứng tỏ rằng

a) $C_4^0 + 2C_4^1 + {2^2}C_4^2 + {2^3}C_4^3 + {2^4}C_4^4 = 81$ $C_4^0 + 2C_4^1 + {2^2}C_4^2 + {2^3}C_4^3 + {2^4}C_4^4 = 81$

b) $C_4^0 - 2C_4^1 + {2^2}C_4^2 - {2^3}C_4^3 + {2^4}C_4^4 = 1$ $C_4^0 - 2C_4^1 + {2^2}C_4^2 - {2^3}C_4^3 + {2^4}C_4^4 = 1$

Hướng dẫn giải

a)

$\begin{array}{l}C_4^0 + 2C_4^1 + {2^2}C_4^2 + {2^3}C_4^3 + {2^4}C_4^4\\ = {1^4}.C_4^0 + {1^3}.2C_4^1 + {1^2}{.2^2}C_4^2 + {1.2^3}C_4^3 + {2^4}C_4^4\\ = {\left( {1 + 2} \right)^4} = {3^4}\end{array}$ $\begin{array}{l}C_4^0 + 2C_4^1 + {2^2}C_4^2 + {2^3}C_4^3 + {2^4}C_4^4\\ = {1^4}.C_4^0 + {1^3}.2C_4^1 + {1^2}{.2^2}C_4^2 + {1.2^3}C_4^3 + {2^4}C_4^4\\ = {\left( {1 + 2} \right)^4} = {3^4}\end{array}$

= 81 (đpcm)

b)

$\begin{array}{l}C_4^0 - 2C_4^1 + {2^2}C_4^2 - {2^3}C_4^3 + {2^4}C_4^4\\ = {1^4}.C_4^0 - {1^3}.2C_4^1 + {1^2}{.2^2}C_4^2 - {1.2^3}C_4^3 + {2^4}C_4^4\\ = {\left( {1 - 2} \right)^4} = {\left( { - 1} \right)^4}\end{array}$ $\begin{array}{l}C_4^0 - 2C_4^1 + {2^2}C_4^2 - {2^3}C_4^3 + {2^4}C_4^4\\ = {1^4}.C_4^0 - {1^3}.2C_4^1 + {1^2}{.2^2}C_4^2 - {1.2^3}C_4^3 + {2^4}C_4^4\\ = {\left( {1 - 2} \right)^4} = {\left( { - 1} \right)^4}\end{array}$

= 1 (đpcm)