Lý thuyết Toán 10 bài 2: Hàm số bậc hai CTST

Sách Chân trời sáng tạo

Chúng tôi xin trân trọng giới thiệu bài Lý thuyết Toán lớp 10 bài 2: Hàm số bậc hai được VnDoc sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

A. Lý thuyết Toán 10 bài 2

1. Hàm số bậc hai

+ Định nghĩa:

Hàm số bậc hai biến x là hàm số cho bởi công thức dạng y = f(x) = ax² + bx + c với a, b, c ∈ R, $a \ne 0.$ $a \ne 0.$

+ Tập xác định: R

Ví dụ: Hàm số nào trong các hàm số sau đây là hàm số bậc hai?

$\begin{array}{l} a)y = 2{x^2} + x\\ b)y = {x^3} + x + 1\\ c)y = \frac{{x + 1}}{{x + 2}}\\ d)y = - 3{x^2} - 1\\ e)y = \sqrt {5 - 2x} \end{array}$ $\begin{array}{l} a)y = 2{x^2} + x\\ b)y = {x^3} + x + 1\\ c)y = \frac{{x + 1}}{{x + 2}}\\ d)y = - 3{x^2} - 1\\ e)y = \sqrt {5 - 2x} \end{array}$

2. Đồ thị hàm số bậc hai

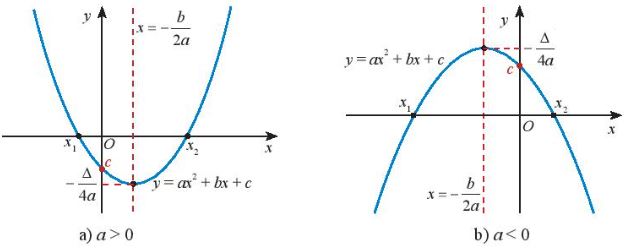
+) Đồ thị hàm số bậc hai $y = f(x) = a{x^2} + bx + c (a \ne 0)$ $y = f(x) = a{x^2} + bx + c (a \ne 0)$ là một parabol (P):

- Đỉnh $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$ $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$

- Trục đối xứng: đường thẳng $x = - \frac{b}{{2a}}$ $x = - \frac{b}{{2a}}$

- Bề lõm: quay lên trên nếu a > 0, quay xuống dưới nếu a < 0

- Cắt Oy tại điểm (0; c)

Chú ý: Nếu PT $a{x^2} + bx + c = 0$ $a{x^2} + bx + c = 0$ có hai nghiệm ${x_1},{x_2}$ ${x_1},{x_2}$ thì đồ thị hàm số $y = a{x^2} + bx + c$ $y = a{x^2} + bx + c$ cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.

+) Vẽ đồ thị

1) Xác định đỉnh $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$ $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$

2) Vẽ trục đối xứng d: $x = - \frac{b}{{2a}}$ $x = - \frac{b}{{2a}}$

3) Tìm tọa độ giao điểm của đồ thị với trục tung (A(0; c)), trục hoành (nếu có).

Xác định $B\left( {\frac{{ - b}}{a};c} \right)$ $B\left( {\frac{{ - b}}{a};c} \right)$ (là điểm đối xứng với A qua d)

4) Vẽ parabol đỉnh S, trục đối xứng d, đi qua các điểm tìm được.

3. Sự biến thiên của hàm số bậc hai

+) Bảng biến thiên

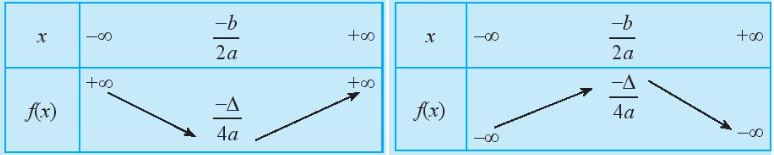
+) Kết luận:

	a > 0	a < 0
Trên khoảng $\left( { - \infty ;\frac{{ - b}}{{2a}}} \right)$ $\left( { - \infty ;\frac{{ - b}}{{2a}}} \right)$	Hàm số nghịch biến	Hàm số đồng biến
Trên khoảng $\left( {\frac{{ - b}}{{2a}}; + \infty } \right)$ $\left( {\frac{{ - b}}{{2a}}; + \infty } \right)$	Hàm số đồng biến	Hàm số nghịch biến
GTLN hoặc GTNN	Đạt GTNN bằng $\frac{{ - \Delta }}{{4a}}$ $\frac{{ - \Delta }}{{4a}}$ tại $x = \frac{{ - b}}{{2a}}$ $x = \frac{{ - b}}{{2a}}$	Đạt GTLN bằng $\frac{{ - \Delta }}{{4a}}$ $\frac{{ - \Delta }}{{4a}}$ tại $x = \frac{{ - b}}{{2a}}$ $x = \frac{{ - b}}{{2a}}$
Tập giá trị	$T = \left[ {\left. {\frac{{ - \Delta }}{{4a}}; + \infty } \right)} \right.$ $T = \left[ {\left. {\frac{{ - \Delta }}{{4a}}; + \infty } \right)} \right.$	$T = \left( {\left. { - \infty ;\frac{{ - \Delta }}{{4a}}} \right]} \right.$ $T = \left( {\left. { - \infty ;\frac{{ - \Delta }}{{4a}}} \right]} \right.$

Ví dụ: Lập bảng biến thiên của hàm số $y = - {x^2} + 4x - 3$ $y = - {x^2} + 4x - 3$. Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.

Giải

Đỉnh S có tọa độ: ${x_s} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.\left( { - 1} \right)}} = 2;{y_s} = - {2^2} + 4.2 - 3 = 1$ ${x_s} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.\left( { - 1} \right)}} = 2;{y_s} = - {2^2} + 4.2 - 3 = 1$

Hay S(2; 1)

Vì hàm số bậc hai có a = -1 < 0 nên ta có bảng biến thiên sau:

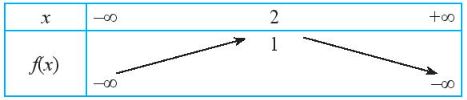
Hàm số đạt giá trị lớn nhất bằng 1 khi x = 2.

4. Ứng dụng của hàm số bậc hai

+) Tầm bay cao và tầm bay xa

Chọn điểm $(0;{y_0})$ $(0;{y_0})$ là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời mặt vợt là:

$y = \frac{{ - g.{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}$ $y = \frac{{ - g.{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}$

Trong đó:

g là giá tốc trọng trường $\approx 9,8\;m/{s^2}$ $\approx 9,8\;m/{s^2}$

$\alpha$ $\alpha$là góc phát cầu (so với phương ngang của mặt đất)

${v_0}$ ${v_0}$là vận tốc ban đầu của cầu

${y_0}$ ${y_0}$là khoảng cách từ vị trí phát cầu đến mặt đất

Quỹ đạo chuyển động của cầu lông là một parabol.

- Vị trí cao nhất tại đỉnh parabol, gọi là tầm bay cao;

- Khoảng cách từ nơi đứng phát cầu đến điểm chạm đất, gọi là tầm bay xa.

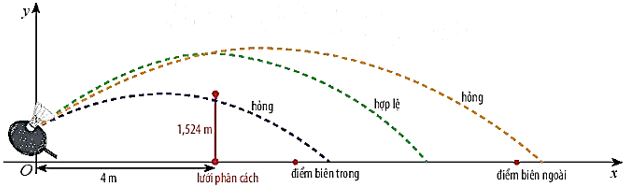
+) Bài toán ứng dụng

Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biến phía sân đối phương thì lần phát cầu được xem là hợp lệ.

B. Bài tập minh họa

Câu 1: Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?

a) $y = 2x(x - 3)$

b) $y = x({x^2} + 2) - 5$ $y = x({x^2} + 2) - 5$

c) $y = - 5(x + 1)(x - 4)$

Hướng dẫn giải

a) $y = 2x(x - 3) = 2{x^2} - 6$ $y = 2x(x - 3) = 2{x^2} - 6$

Hàm số có lũy thừa bậc cao nhất của x là bậc hai

b) $y = x({x^2} + 2) - 5 = {x^3} + 2x - 5$ $y = x({x^2} + 2) - 5 = {x^3} + 2x - 5$

Hàm số có lũy thừa bậc cao nhất của x là bậc ba

c) $y = - 5(x + 1)(x - 4) = - 5{x^2} + 15x + 20$ $y = - 5(x + 1)(x - 4) = - 5{x^2} + 15x + 20$

Hàm số có lũy thừa bậc cao nhất của x là bậc hai

Câu 2: Vẽ đồ thị hàm số $y = {x^2} - 4x + 3$ $y = {x^2} - 4x + 3$

Hướng dẫn giải

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = f(x) = {x^2} - 4x + 3$ $y = f(x) = {x^2} - 4x + 3$ là một parabol (P1):

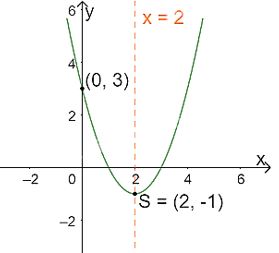
+ Có đỉnh S với hoành độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.$

+ Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay lên trên vì a = 1 > 0

+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ta vẽ được đồ thị như hình dưới.

Câu 3: Tìm khoảng đồng biến, khoảng nghịch biến của hàm số $y = 2{x^2} - 6x + 11.$ $y = 2{x^2} - 6x + 11.$ Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?

Hướng dẫn giải

Đỉnh S có tọa độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 6)}}{{2.2}} = \frac{3}{2};{y_S} = 2.{\left( {\frac{3}{2}} \right)^2} - 6.\frac{3}{2} + 11 = \frac{{13}}{2}.$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 6)}}{{2.2}} = \frac{3}{2};{y_S} = 2.{\left( {\frac{3}{2}} \right)^2} - 6.\frac{3}{2} + 11 = \frac{{13}}{2}.$

Hay $S\left( {\frac{3}{2};\frac{{13}}{2}} \right).$ $S\left( {\frac{3}{2};\frac{{13}}{2}} \right).$

Vì hàm số bậc hai có a = 2 > 0 nên ta có bảng biến thiên sau:

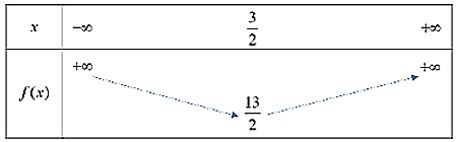
Hàm số đồng biến trên khoảng $(\frac{3}{2}; + \infty )$ $(\frac{3}{2}; + \infty )$ và nghịch biến trên khoảng $( - \infty ;\frac{3}{2})$ $( - \infty ;\frac{3}{2})$

Hàm số đạt giá trị nhỏ nhất bằng $\frac{{13}}{2}$ $\frac{{13}}{2}$ khi $x = \frac{3}{2}$ $x = \frac{3}{2}$

Do đó hàm số không thể đạt giá trị bằng -1 vì $- 1 < \frac{{13}}{2}.$ $- 1 < \frac{{13}}{2}.$