Toán 10 Bài 2: Hàm số bậc hai

Toán 10 Bài 3: Hàm số bậc hai được VnDoc biên soạn bao gồm hướng dẫn lý thuyết và hướng dẫn giải cho từng bài tập sách giáo khoa lớp 10 mới. Mời các bạn cùng theo dõi bài viết.

I. Giải Toán 10 bài Hàm số bậc hai sách mới

1. Giải Toán 10 Bài 2: Hàm số bậc hai sách CTST

Mời bạn đọc cùng tham khảo thêm tại Giải Toán 10 Bài 2: Hàm số bậc hai

Bài 1 trang 56 SGK Toán 10 CTST

Hàm số nào sau đây là hàm số bậc hai?

a) y = 9x² + 5x + 4;

b) y = 3x³ + 2x + 1;

c) y = -4 (x + 2)³ + 2 (2x³ + 1) + 5;

d) y = 5x² + \(\sqrt x\) + 2.

Lời giải

a) y = 9x² + 5x + 4 là hàm số bậc hai với a = 9, b = 5 và c = 4.

b) y = 3x³ + 2x + 1 không là hàm số bậc hai vì bậc cao nhất là bậc ba.

c) y = -4(x + 2)³ + 2(2x³ + 1) + 5

⇔ y = -4 (x³ + 3x².2 + 3.x.2² + 2³) + 4x³ + 2 + 5

⇔ y = -4x³ – 24x² – 48x – 32 + 4x³ + 2 + 5

⇔ y = – 24x² – 48x – 25

Là hàm số bậc hai với a = -24, b = -48, c = -25.

d) y = 5x² + \(\sqrt x\) + 2 không là hàm số bậc hai vì có chứa hạng tử \(\sqrt x\).

Bài 2 trang 56 SGK Toán 10 CTST

Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai.

a) y = mx⁴ + (m + 1)x² + x + 3;

b) y = (m – 2)x³ + (m – 1)x² + 5.

Lời giải

a) Để hàm số y = mx⁴ + (m + 1)x² + x + 3 là hàm bậc hai thì hệ số của x⁴ phải bằng 0 và hệ số của x² phải khác không tức là: \(\left\{\begin{array}{l}m\;=\;0\\m\;+\;1\;\neq\;0\end{array}\right.\;\Leftrightarrow\;\left\{\begin{array}{l}m\;=\;0\\m\;\neq\;-\;1\end{array}\right.\;\Leftrightarrow\;m\;=\;0\;\;\)

Vậy với m = 0 thì hàm số đã cho là hàm số bậc hai.

b) Để hàm số y = (m – 2)x³ + (m – 1)x² + 5 là hàm số bậc hai thì hệ số của x³ phải bằng 0 và hệ số của x² phải khác không tức là:

\(\left\{\begin{array}{l}m\;-\;2\;=\;0\\m\;-\;1\;\neq\;0\end{array}\right.\;\Leftrightarrow\;\left\{\begin{array}{l}m\;=\;2\\m\;\neq\;1\end{array}\right.\;\Leftrightarrow\;m\;=\;2\)

Vậy với m = 2 thì hàm số đã cho là hàm số bậc hai.

Bài 3 trang 56 SGK Toán 10 CTST

Lập bảng biến thiên của hàm số y = x² + 2x + 3. Hàm số này có giá trị lớn nhất hay nhỏ nhất? Tìm giá trị đó.

Lời giải

Xét hàm số bậc hai: y = x² + 2x + 3 có a = 1, b = 2 và c = 3.

Đỉnh S có tọa độ x_s = \(\frac{-b}{2a}\) = \(\frac{-2}{2.1}\) = −1, y_s = (-1)² + 2.(-1) + 3 = 2. Hay S (-1; 2).

Vì hàm số bậc hai có a = 1 > 0 nên ta có bảng biến thiên sau:

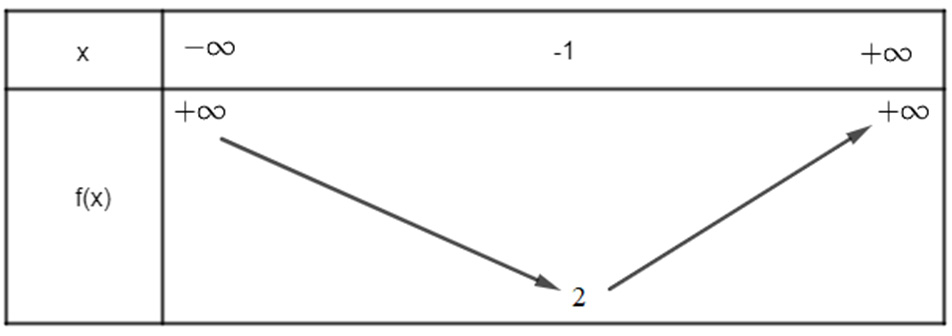
Hàm số có giá trị nhỏ nhất bằng 2 khi x = -1.

Bài 4 trang 56 SGK Toán 10 CTST

Cho hàm số bậc hai y = f(x) = ax² + bx + c có f(0) = 1, f(1) = 2, f(2) = 5.

a) Hãy xác định giá trị của các hệ số a, b, c.

b) Xác định tập giá trị và khoảng biến thiên của hàm số.

Lời giải

Ta có

f(0) = a.0² + b.0 + c = 1 ⇔ c = 1.

f(1) = a.1² + b.1 + c = 2 ⇔ a + b + c = 2.

f(2) = a.2² + b.2 + c = 5 ⇔ 4a + 2b + c = 5.

Khi đó, ta có hệ phương trình:

\(\left\{\begin{array}{l}c\;=\;1\\a\;+\;b\;+\;c\;=\;2\\4\;a\;+\;2\;b\;+\;c\;=\;5\end{array}\right.\;\Leftrightarrow\;\left\{\begin{array}{l}c\;=\;1\\a\;+\;b\;=\;1\\4\;a\;+\;2\;b\;=\;4\end{array}\right.\;\Leftrightarrow\;\left\{\begin{array}{l}c\;=\;1\\a\;+\;b\;=\;1\\2\;a\;+\;b\;=\;2\end{array}\right.\;\Leftrightarrow\;\left\{\begin{array}{l}c\;=\;1\\a\;=\;1\\b\;=\;0\end{array}\right.\)

Vậy a = 1, b = 0 và c = 1.

b) Với a = 1, b = 0 và c = 1 thì ta có hàm số: y = x2 + 1.

Xét hàm số bậc hai: y = x2 + 1, có:

Đỉnh S có tọa độ x_s = \(\frac{-b}{2a}\) = \(\frac{-0}{2.1}\) = 0, y_s = 0² + 1 = 1. Hay S (0; 1).

Vì hàm số bậc hai có a = 1 > 0 nên ta có bảng biến thiên sau:

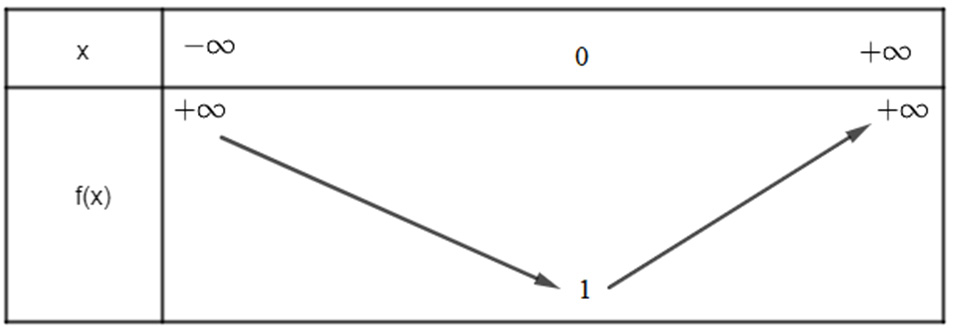
Dựa vào bảng biến thiên ta có:

Hàm số có giá trị nhỏ nhất bằng 1 khi x = 0. Do đó tập giá trị của hàm số là [1; \(+\infty\)).

Hàm số nghịch biến trên khoảng (\(-\infty\);0) và đồng biến trên khoảng (0; \(+\infty\)).

Bài 5 trang 56 SGK Toán 10 CTST

Cho hàm số y = 2x² + x + m. Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.

Lời giải

Xét hàm số y = 2x² + x + m có a = 2, b = 1 và c = m.

Điểm đỉnh S có tọa độ x_S = \(\frac b{2a}\;=\;-\frac1{2.2}\;=\;-\frac14\), y_S \(2.\;(\;-\;\frac14\;){}^2\;+\;(\;-\;\frac{1\;}4)\;+\;m\;=\;m\;-\;\frac18\)

Hàm số có a = 2 > 0 nên giá trị nhỏ nhất của hàm số là m – \(\frac18\)

Mà giá trị nhỏ nhất bằng 5 nên m –\(\frac18\) = 5 ⇔ m = \(\frac{41}8\)

Vậy với m = \(\frac{41}8\) thì giá trị nhỏ nhất của hàm số là 5.

Bài 6 trang 56 SGK Toán 10 CTST

Vẽ đồ thị các hàm số sau:

a) y = 2x² + 4x – 1;

b) y = -x² + 2x + 3;

c) y = -3x² + 6x;

d) y = 2x² – 5.

Lời giải

a) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x² + 4x – 1 là một parabol (P):

- Có đỉnh S với hoành độ x_S = -1, tung độ y_S = -3;

- Có trục đối xứng là đường thẳng x = -1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay lên trên vì a > 0;

- Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).

Ngoài ra, phương trình 2x² + 4x – 1 = 0 có hai nghiệm phân biệt x₁ = \(\frac{-2\;+\;\sqrt6}2\)  và x₂ =

\(\frac{-2\hspace{0.278em}-\hspace{0.278em}\sqrt6}2\)  nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ  \(\left(\frac{-2\;+\;\sqrt6}2;\;0\right)\) và \((\frac{-2\hspace{0.278em}-\hspace{0.278em}\sqrt6}2;\hspace{0.278em}0)\)

Ta được đồ thị hàm số như sau:

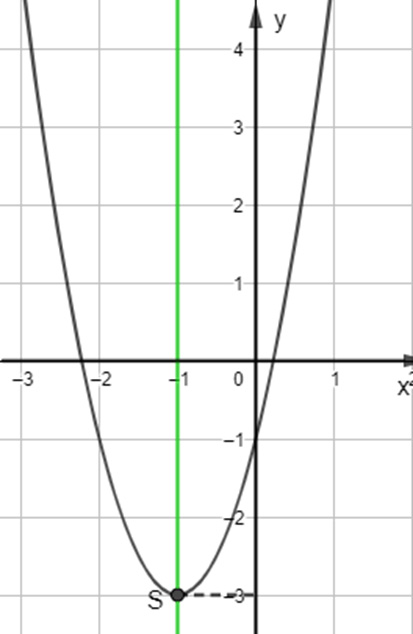
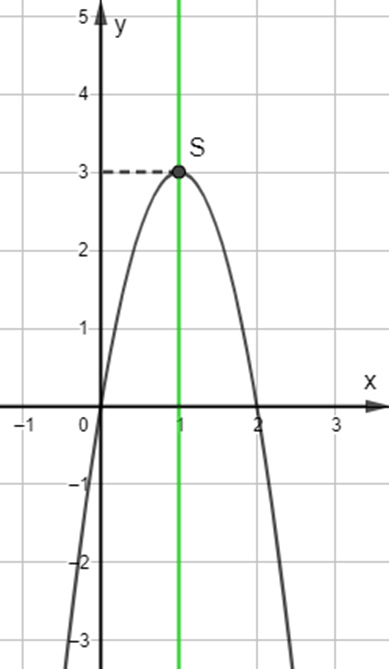
b) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = -x² + 2x + 3 là một parabol (P):

- Có đỉnh S với hoành độ x_S = 1, tung độ y_S = 4;

- Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay xuống dưới vì a < 0;

- Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ngoài ra, phương trình -x² + 2x + 3 = 0 có hai nghiệm phân biệt x₁ = 3 và x₂ = -1 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (3; 0) và (-1; 0).

Ta được đồ thị hàm số như sau:

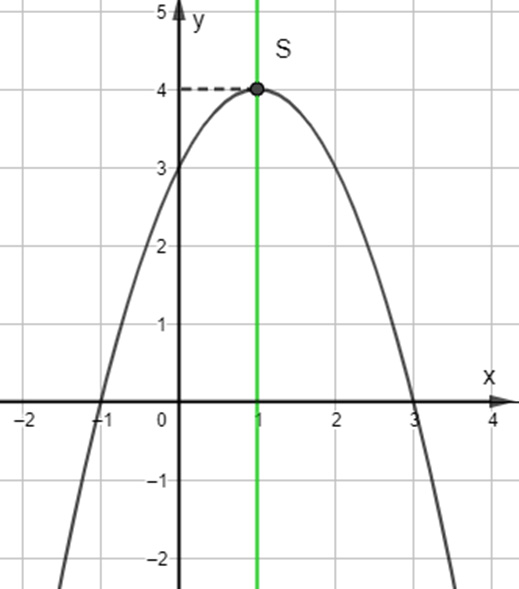
c) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = -3x² + 6x là một parabol (P):

- Có đỉnh S với hoành độ x_S = 1, tung độ y_S = 3;

- Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay xuống dưới vì a < 0;

- Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua điểm có tọa độ (0; 0).

Ngoài ra, phương trình -3x² + 6x = 0 có hai nghiệm phân biệt x₁ = 0 và x₂ = 2 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (0; 0) và (2; 0).

Ta được đồ thị hàm số như sau:

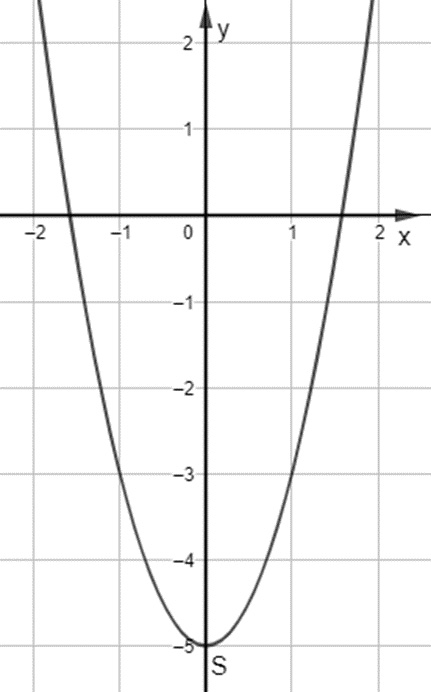
d) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x² – 5 là một parabol (P):

- Có đỉnh S với hoành độ x_S = 0, tung độ y_S = -5;

- Có trục đối xứng là đường thẳng x = 0 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay lên trên vì a > 0;

- Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).

Ngoài ra, phương trình 2x² – 5 = 0 có hai nghiệm phân biệt x₁ = \(\sqrt{\frac52}\) và x₂ = \(-\sqrt{\frac52}\)

nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (\(\sqrt{\frac52}\); 0) và (\(-\sqrt{\frac52}\); 0).

Ta được đồ thị hàm số như sau:

Bài 7 trang 56 SGK Toán 10 CTST

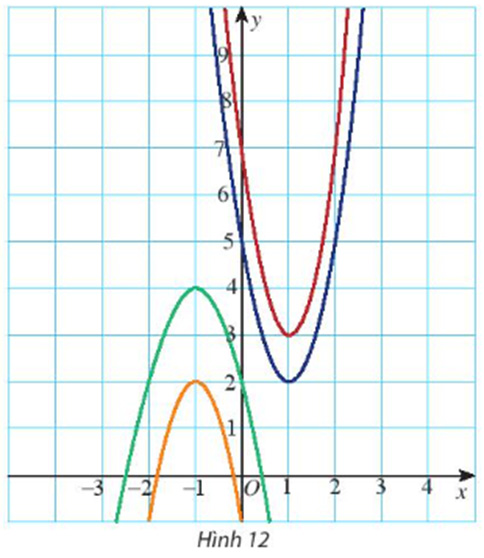
Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.

(P₁): y = - 2x² – 4x + 2;

(P₂): y = 3x² – 6x + 5;

(P₃): y = 4x² – 8x + 7;

(P₄): y = -3x² – 6x + 1.

Lời giải

+) (P₁): y = - 2x² – 4x + 2

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = - 2x² – 4x + 2 là một parabol (P₁):

- Có đỉnh S với hoành độ x_S = -1, tung độ y_S = 4;

- Có trục đối xứng là đường thẳng x = -1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay xuống dưới vì a < 0;

- Cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2).

Quan sát trên hình vẽ, ta thấy đồ thị tương thích với hàm số (P₁) là đường cong màu xanh lá cây.

+) (P₂): y = 3x² – 6x + 5;

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = 3x² – 6x + 5 là một parabol (P₂):

- Có đỉnh S với hoành độ x_S = 1, tung độ y_S = 2;

- Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay lên trên vì a > 0;

- Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).

Quan sát trên hình vẽ, ta thấy đồ thị tương thích với hàm số (P₂) là đường cong màu xanh dương.

+) (P₃): y = 4x² – 8x + 7:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = 4x² – 8x + 7 là một parabol (P₃):

- Có đỉnh S với hoành độ x_S = 1, tung độ y_S = 3;

- Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay lên trên vì a > 0;

- Cắt trục tung tại điểm có tung độ bằng 7, tức là đồ thị đi qua điểm có tọa độ (0; 7).

Quan sát trên hình vẽ, ta thấy đồ thị tương thích với hàm số (P₃) là đường cong màu đỏ.

+) (P₄): y = -3x² – 6x + 1:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = -3x² – 6x – 1 là một parabol (P₄):

- Có đỉnh S với hoành độ x_S = -1, tung độ y_S = 2;

- Có trục đối xứng là đường thẳng x = -1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay xuống dưới vì a < 0;

- Cắt trục tung tại điểm có tung độ bằng 1, tức là đồ thị đi qua điểm có tọa độ (0; -1).

Quan sát trên hình vẽ, ta thấy đồ thị tương thích với hàm số (P₄) là đường cong màu cam.

Bài 8 trang 57 SGK Toán 10 CTST

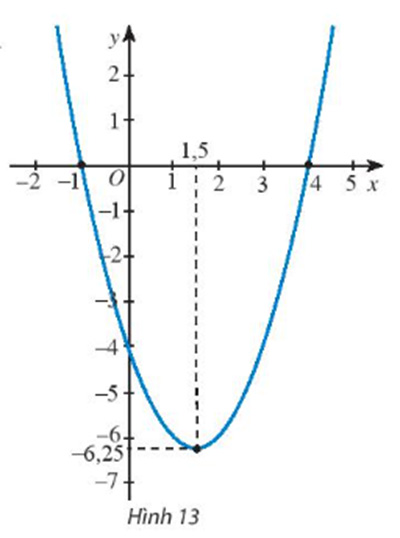
Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.

Lời giải

Dựa vào hình vẽ ta thấy:

Đồ thị hàm số có dạng parabol nên hàm số có dạng y = ax² + bx + c với a, b, c ∈ và a ≠ 0. Hơn nữa đồ thị hàm số có bề lõm hướng lên trên nên a > 0.

Đồ thị hàm số cắt trục tung tại điểm tọa độ (0; -4) nên ta có: 4 = a.0² + b.0 + c ⇔ c = 4.

Điểm đỉnh S của đồ thị hàm số có tọa độ x_S = 1,5 và y_S = -6.25

\(\Rightarrow x_S\;=\;-\frac b{2a}\;=\;1,5\;\Leftrightarrow\;b\;=\;-3a\)

Đồ thị hàm số cắt trục hoành tại hai điểm (-1; 0) và (4; 0) nên thay x = -1 và y = 0 vào hàm số ta được: 0 = a(-1)² + b(-1) + c

⇔ 0 = a – b + c

Mà b = – 3a và c = 4 nên ta có: a + 3a + 4 = 0 ⇔ a = 1 ⇒ b = -3.

Vậy hàm số cần tìm là y = x² – 3x + 4.

Bài 9 trang 57 SGK Toán 10 CTST

Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.

Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:

- Dây dài nhất là 5m, dây ngắn nhất là 0,8m. Khoảng cách giữa các dây bằng nhau.

- Nhịp cầu dài 30m.

- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Lời giải

Hình dây văng có dạng parabol, nên ta có hình vẽ sau:

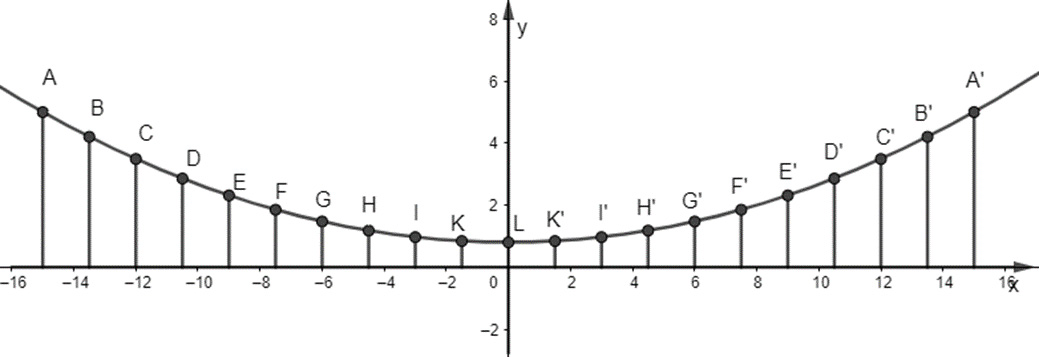
Độ dài của dây cáp tương ứng với tung độ của các điểm A, B, C, D, E, F, G, H, I, K, L, K’, I’, H’, G’, F’, E’, D’, C’, B’, A’.

Dây dài nhất tương ứng với điểm A và A’ trên đồ thị. Khi đó A (-15; 5) và A’ (15; 5).

Dây ngắn nhất trên đồ thị tương ứng với điểm L trên đồ thị. Khi đó L(0; 0,8).

Gọi hàm số đi qua các điểm này có dạng y = ax² + bx + c.

Ta có hàm số đi qua A(-15; 5) nên thay x = -15 và y = 5 ta có: 225a – 15b + c = 5;

Ta có hàm số đi qua A(15; 5) nên thay x = 15 và y = 5 ta có: 225a + 15b + c = 5;

Ta có hàm số đi qua điểm L(0; 1) nên thay x = 0 và y = 1 ta có: b + c = 1;

Khi đó ta có hệ phương trình: \(\left\{\begin{array}{l}225\;a\;-\;15\;b\;+\;c\;=\;5\;\\225\;a\;+\;15\;b\;+\;c\;=\;5\;\\c\;=\;1\end{array}\right.\;\Leftrightarrow\;\left\{\begin{array}{l}a\;=\;\frac4{225}\;\;\\b\;=\;0\\c\;=\;1\end{array}\right.\)

Suy ra ta có hàm số y = \(\frac4{225}\;x^2\;+\;1\)

Hàm số có trục đối xứng là x = 0 hay chính là trục tung. Do đó các điểm A, B, C, D, E, F, G, H, I, K đối xứng với các điểm A’, B’, C’, D’, E’, F’, G’, H’, I’, K’ qua trục tung. Vì thế các điểm này có cùng tung độ.

Vì nhịp cầu dài 30 m nên khoảng cách giữa các dây cáp là: 30: 20 = 1,5 m.

Do đó hoành độ các điểm K’, I’, H’, G’, F’, E’, D’, C’, B’, A’ lần lượt là:

x_K’ = 1,5 ⇒ y_K’ = \(\frac{26}{25}\)  ⇒ K’ = \(\left(\frac32;\frac{26}{25}\right)\) Do đó độ dài dây cáp ở điểm K và K’ là \(\frac{26}{25}\)

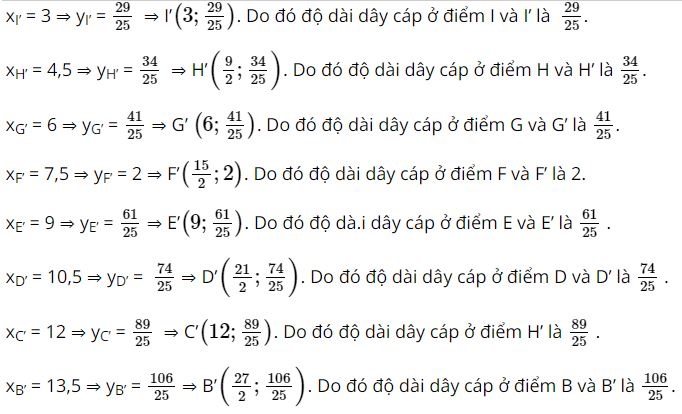
x_A’ = 15 ⇒ y_A’ = 5 ⇒ A’. Do đó độ dài dây cáp ở điểm A và A’ là 5.

Vì cần tính thêm 5% chiều dài mỗi sợi dây cap để neo cố định nên tổng độ dài các dây cáp là:

Vậy tổng độ dài dây cáp cần dùng \(\frac{2667}{50}\)m.

2. Giải Toán 10 Bài 2: Hàm số bậc hai sách CD

Mời bạn đọc cùng tham khảo thêm: Giải Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng CD

Bài 1 trang 43 SGK Toán 10 CD

Trong các hàm số sau, hàm số nào là hàm số bậc hai? Với những hàm số bậc hai đó, xác định \(a,b,c\) lần lượt là hệ số của \({x^2}\), hệ số của x và hệ số tự do.

\(a)\ y = - 3{x^2}\)

\(b)\ y = 2x\left( {{x^2} - 6x + 1} \right)\)

\(c)\ y = 4x\left( {2x - 5} \right)\)

Lời giải

a) Hàm số \(y = - 3{x^2}\)là hàm số bậc hai.

\(y = - 3.{x^2} + 0.x + 0\)

Hệ số a = - 3, b = 0, c = 0.

b) Hàm số \(y = 2x\left( {{x^2} - 6x + 1} \right) \Leftrightarrow y = 2{x^3} - 12{x^2} + 2x\) có số mũ cao nhất là 3 nên không là hàm số bậc hai.

c) Hàm số \(y = 4x\left( {2x - 5} \right) \Leftrightarrow y = 8{x^2} - 20x\) có số mũ cao nhất là 2 nên là hàm số bậc hai.

Hệ số a = 8, b = - 20, c = 0

Bài 2 trang 43 SGK Toán 10 CD

Xác định parabol \(y = a{x^2} + bx + 4\) trong mỗi trường hợp sau:

a) Đi qua điểm \(M\left( {1;12} \right)\) và \(N\left( { - 3;4} \right)\)

b) Có đỉnh là \(I\left( { - 3; - 5} \right)\)

Lời giải

) Thay tọa độ điểm \(M\left( {1;12} \right)\) và \(N\left( { - 3;4} \right)\) ta được:

\(\begin{array}{l}\left\{ \begin{array}{l}a{.1^2} + b.1 + 4 = 12\\a.{\left( { - 3} \right)^2} + b.\left( { - 3} \right) + 4 = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a + b = 8\\9a - 3b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 6\end{array} \right.\end{array}\)

Vậy parabol là \(y = 2{x^2} + 6x + 4\)

b) Hoành độ đỉnh của parabol là \(\frac{{ - b}}{{2a}}\)

Nên ta có: \(\frac{{ - b}}{{2a}} = - 3 \Leftrightarrow b = 6a (1)\)

Thay tọa độ điểm I vào ta được:

\(\begin{array}{l} - 5 = a.{\left( { - 3} \right)^2} + b.\left( { - 3} \right) + 4\\ \Leftrightarrow 9a - 3b = - 9\\ \Leftrightarrow 3a - b = - 3\left( 2 \right)\end{array}\)

Từ (1) và (2) ta được hệ

\(\begin{array}{l}\left\{ \begin{array}{l}b = 6a\\3a - b = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6a\\3a - 6a = - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b = 6a\\a = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6\\a = 1\end{array} \right.\end{array}\)

Vậy parabol là \(y = {x^2} + 6x + 4.\)

Bài 3 trang 43 SGK Toán 10 CD

Vẽ đồ thị của mỗi hàm số sau:

\(a) y = 2{x^2} - 6x + 4\)

\(b) y = - 3{x^2} - 6x - 3\)

Lời giải

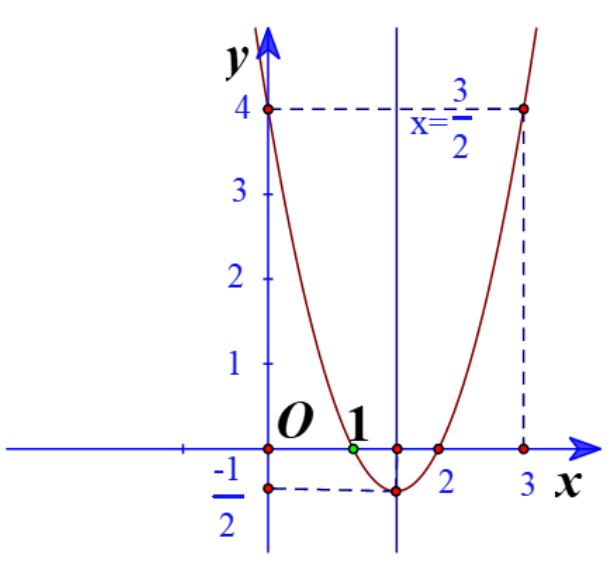
a) Đồ thị hàm số có đỉnh \(I\left( {\frac{3}{2}; - \frac{1}{2}} \right)\)

Trục đối xứng là \(x = \frac{3}{2}\)

Giao điểm của parabol với trục tung là (0;4)

Giao điểm của parabol với trục hoành là (2;0) và (1;0)

Điểm đối xứng với điểm (0;4) qua trục đối xứng \(x = \frac{3}{2}\) là \(\left( {3;4} \right)\)

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

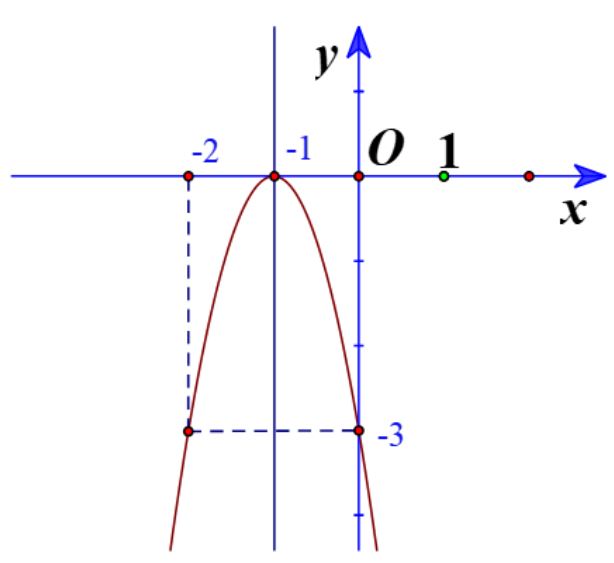
b) Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\)

Trục đối xứng là x = - 1

Giao điểm của parabol với trục tung là (0;-3)

Giao điểm của parabol với trục hoành là \(I\left( { - 1;0} \right)\)

Điểm đối xứng với điểm (0;-3) qua trục đối xứng x = - 1 là (-2;-3)

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

Bài 4 trang 43 SGK Toán 10 CD

Cho đồ thị hàm số bậc hai ở Hình 15.

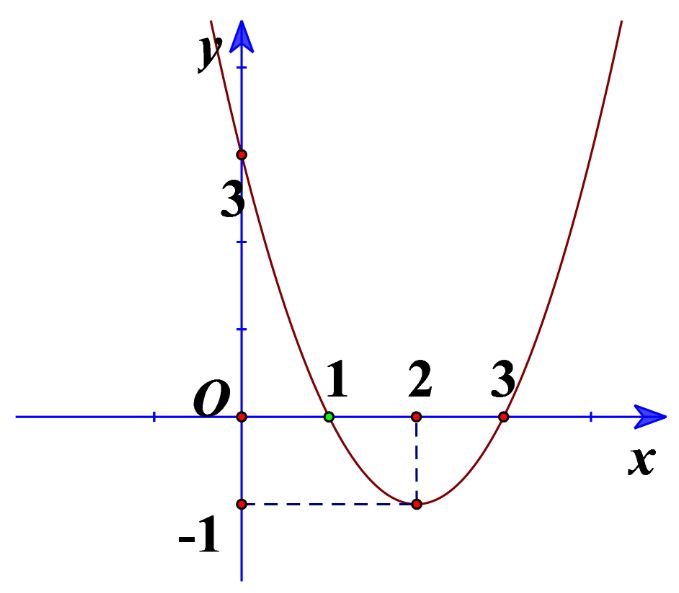
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.

b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.

c) Tìm công thức xác định hàm số.

Lời giải

a) Trục đối xứng là đường thẳng x = 2

Đỉnh là \(I\left( {2; - 1} \right)\)

b) Từ đồ thị ta thấy trên khoảng \(\left( { - \infty ;2} \right)\) thì hàm số đi xuống nên hàm số nghịch biến trên \(\left( { - \infty ;2} \right).\)

Trên khoảng \(\left( {2; + \infty } \right)\) thì hàm số đi xuống nên đồng biến trên \(\left( {2; + \infty } \right).\)

c) ) Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)

Đồ thị hàm số có đỉnh là \(I\left( {2; - 1} \right)\) nên ta có:

\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\end{array} \right.\)

Ta lại có điểm \(\left( {1;0} \right)\) thuộc đồ thị nên ta có: a + b + c = 0

Vậy ta có hệ sau:

\(\left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\\a + b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2.\left( { - 4a} \right) + c = - 1\\a + \left( { - 4a} \right) + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\c - 4a = - 1\\c - 3a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\a = 1\\c = 3\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}b = - 4\\a = 1\\c = 3\end{array} \right.\)

Vậy parabol là \(y = {x^2} - 4x + 3\)

Bài 5 trang 43 SGK Toán 10 CD

Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:

\(a)\ y = 5{x^2} + 4x - 1\)

\(b)\ y = - 2{x^2} + 8x + 6\)

Lời giải

a) Hệ số \(a = 5 > 0,b = 4 \Rightarrow \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.5}} = \frac{{ - 2}}{5}\)

Vậy hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{{ - 2}}{5}} \right)\) và đồng biến trên \(\left( {\frac{{ - 2}}{5}; + \infty } \right)\)

b) Ta có a = - 2 < 0,b = 8

\(\Rightarrow - \frac{b}{{2a}} = \frac{{ - 8}}{{2.\left( { - 2} \right)}} = 2\)

Vậy hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;2} \right)\) và nghịch biến trên khoảng \(\left( {2; + \infty } \right)\)

Bài 6 trang 43 SGK Toán 10 CD

Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ toạ độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 (x và y tính bằng mét), chân kia của cổng ở vị trí có toạ độ (162;0). Biết một điểm M trên cổng có toạ độ là (10;43). Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.

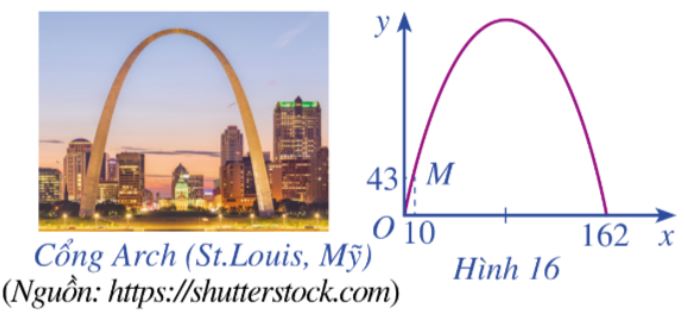
Lời giải

Từ đồ thị ta thấy các điểm thuộc đồ thị là: \(A\left( {0;0} \right),B\left( {10;43} \right),B\left( {162;0} \right).\)

Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)

Thay tọa độ các điểm A, B, C vào ta được hệ:

\(\left\{ \begin{array}{l}a{.0^2} + b.0 + c = 0\\a{.10^2} + b.10 + c = 43\\a{.162^2} + b.162 + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\100a + 10b = 43\\{162^2}a + 162b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = - \frac{{43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.\)

Từ đố ta có \(y = - \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\)

Hoành độ đỉnh của đồ thị là: \(x = - \frac{b}{{2a}} = 81\)

Khi đó: \(y = - \frac{{43}}{{1520}}{.81^2} + \frac{{3483}}{{760}}.81 \approx 186(m)\)

Vậy chiều cao của cổng là 186m.

II. Giải Toán 10 bài Hàm số bậc hai sách cũ

A. Lí thuyết Hàm số bậc hai

1. Ôn tập về hàm số bậc hai

Hàm số bậc hai có dạng: _{\(y=a{{x}^{2}}+bx+c,\left( a\ne 0 \right)\)}

• Tập xác định \(D=\mathbb{R}\)
• Có biệt thức \(\triangle =b^2-4ac\)
• Đồ thị của hàm số \(y=a{{x}^{2}}+bx+c,\left( a\ne 0 \right)\) là một đường Parabol có đỉnh là điểm \(I\left( \frac{-b}{2a},\frac{-\Delta }{4a} \right)\)
• Trục đối xứng là đường thẳng \(x=\frac{-b}{2a}\)
• Parabol này quay bề lõm lên trên nếu a > 0, quay xuống dưới nếu a < 0

2. Cách vẽ Parabol đồ thị của hàm số bậc hai

Bước 1: Xác định tọa độ đỉnh \(I\left( \frac{-b}{2a},\frac{-\Delta }{4a} \right)\)

Bước 2: Vẽ trục đối xứng \(x=\frac{-b}{2a}\)

Bước 3: Xác định tọa độ các giao điểm của Parabol với trục tung và trục hoành (nếu có)

Bước 4: Vẽ parabol

3. Chiều biến thiên của hàm số bậc hai

+ Nếu a > 0 thì hàm số nghịch biến trên khoảng _{\(\left ( -\infty,-\dfrac{b}{2a} \right )\)}, hàm số đồng biến trên khoảng \(\left (-\dfrac{b}{2a}, +\infty \right)\)

+ Nếu a < 0 thì hàm số nghịch biến trên khoảng _{\(\left ( -\dfrac{b}{2a},+\infty\right )\)}, hàm số đồng biến trên khoảng \(\left ( -\infty,-\dfrac{b}{2a}\right )\)

- Đồ thị hàm số \(y=a^2+bx+c,a\neq0\) suy ra từ đồ thị hàm số \(y=ax^2\)bằng cách:

+ Tịnh tiến song song với trục hoành \(\left | \dfrac{b}{2a} \right |\) đơn vị về bên trái nếu \(\dfrac{b}{2a}>0\), về bên phải nếu \(\dfrac{b}{2a}<0\)

+ Tịnh tiến song song với trục tung \(\left | -\dfrac{\Delta}{4a}\right |\) đơn vị lên trên nếu \(-\dfrac{\Delta}{4a}>0\) và xuống dưới nếu \(-\dfrac{\Delta}{4a}<0\)

B. Giải SGK Toán 10 Bài 3

Trong Sách giáo khoa Toán lớp 10, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 10. Mời các bạn học sinh tham khảo:

• Giải bài tập trang 49, 50 SGK Đại số 10 chương 2: Hàm số bậc hai

C. Giải SBT Toán 10 Bài 3

Sách bài tập Toán 10 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:

• Giải bài tập Toán 10 SBT bài 3 chương 2

D. Bài tập trắc nghiệm Toán 10 Hàm số bậc hai

Để ôn tập lại kiến thức cũng như rèn luyện nâng cao hơn về bài tập của phần Hàm số này, VnDoc xin gửi tới các bạn học sinh Tài liệu Bài tập về Hàm số bậc hai do VnDoc biên soạn. Qua đó sẽ giúp các bạn học sinh hiểu sâu hơn và nắm rõ hơn lý thuyết cũng như bài tập của bài học này. Mời các bạn học sinh tham khảo:

• Trắc nghiệm hàm số bậc hai môn Toán lớp 10

------------------------------------

Trên đây VnDoc đã giới thiệu tới các bạn bài Toán 10 Bài 3: Hàm số bậc hai. Hy vọng với tài liệu này các bạn học sinh sẽ nắm chắc kiến thức vận dụng tốt vào giải bài tập từ đó học tốt môn Toán lớp 10. Chúc các bạn học tốt và nhớ thường xuyên tương tác để cập nhật được nhiều bài tập hay bổ ích nhé!

Ngoài ra, VnDoc giới thiệu thêm tới bạn đọc tham khảo một vài tài liệu liên quan tới chương trình lớp 10: Ngữ Văn 10, Tiếng Anh lớp 10, Vật lý lớp 10,...