Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Lý thuyết Toán 10 bài 3: Tích của một số với một vectơ CTST

Sách Chân trời sáng tạo

Bài trước

Tải về

Bài sau

VnDoc xin giới thiệu bài Lý thuyết Toán lớp 10 bài 3: Tích của một số với một vectơ được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Bài 3: Tích của một số với một vectơ

A. Lý thuyết Toán 10 bài 3
- 1. Tích của một số với một vecto và các tính chất
- 2. Điều kiện để hai vecto cùng phương
B. Bài tập minh họa
C. Trắc nghiệm Toán 10 bài 3

A. Lý thuyết Toán 10 bài 3

1. Tích của một số với một vecto và các tính chất

+) Tích của một số thực k với một vecto $\overrightarrow a \ne \overrightarrow 0$ $\vec{a} \neq \vec{0}$ là một vecto, kí kiệu là $k\overrightarrow a .$ $k \vec{a} .$

+) Vecto $k\overrightarrow a$ $k \vec{a}$ có độ dài bằng $\left| k \right|\left| {\overrightarrow a } \right|$ $| k | | \vec{a} |$ và cùng hướng với vecto $\overrightarrow a,$ $\vec{a},$ nếu k > 0, ngược hướng với vecto $\overrightarrow a$ $\vec{a}$ nếu k < 0

+) Quy ước: $0\;\overrightarrow a = \overrightarrow 0 và k\;\overrightarrow 0 = \overrightarrow 0$ $0 \vec{a} = \vec{0} v à k \vec{0} = \vec{0}$

+) Tính chất: Với hai vecto $\overrightarrow a ,\overrightarrow b$ $\vec{a}, \vec{b}$ và hai số thực k, t ta luôn có:

$\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a = k\overrightarrow a + t\overrightarrow a \\k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b ;\quad k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \\1\;\overrightarrow a = \overrightarrow a ;\;\;( - 1)\;\overrightarrow a = - \,\overrightarrow a \end{array}$ $\begin{array}{l} k (t \vec{a}) = (k t) \vec{a} \\ (k + t) \vec{a} = k \vec{a} + t \vec{a} \\ k (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b}; k (\vec{a} - \vec{b}) = k \vec{a} - k \vec{b} \\ 1 \vec{a} = \vec{a}; (- 1) \vec{a} = - \vec{a} \end{array}$

Ví dụ: Thực hiện các phép toán vecto sau:

$\begin{array}{l} a)5\left( {\overrightarrow u + \overrightarrow v } \right)\\ b)\left( {x + 2} \right)\overrightarrow a \\ c) - 3\left( {4\overrightarrow e } \right)\\ d)\overrightarrow c - 2\overrightarrow c \end{array}$ $\begin{array}{l} a) 5 (\vec{u} + \vec{v}) \\ b) (x + 2) \vec{a} \\ c) - 3 (4 \vec{e}) \\ d) \vec{c} - 2 \vec{c} \end{array}$

Giải

$\begin{array}{l} a)5\left( {\overrightarrow u + \overrightarrow v } \right) = 5\overrightarrow u + 5\overrightarrow v \\ b)\left( {x + 2} \right)\overrightarrow a = x\overrightarrow a + 2\overrightarrow a \\ c) - 3\left( {4\overrightarrow e } \right) = \left( { - 3.4} \right)\overrightarrow e = - 12\overrightarrow e \\ d)\overrightarrow c - 2\overrightarrow c = \left( {1 - 2} \right)\overrightarrow c = \left( { - 1} \right)\overrightarrow c = - \overrightarrow c \end{array}$ $\begin{array}{l} a) 5 (\vec{u} + \vec{v}) = 5 \vec{u} + 5 \vec{v} \\ b) (x + 2) \vec{a} = x \vec{a} + 2 \vec{a} \\ c) - 3 (4 \vec{e}) = (- 3.4) \vec{e} = - 12 \vec{e} \\ d) \vec{c} - 2 \vec{c} = (1 - 2) \vec{c} = (- 1) \vec{c} = - \vec{c} \end{array}$

2. Điều kiện để hai vecto cùng phương

Hai vecto $\overrightarrow a$ $\vec{a}$ và $\overrightarrow b (\overrightarrow b)$ $\vec{b} (\vec{b})$ khác $\overrightarrow 0$ $\vec{0}$ cùng phương khi và chỉ khi tồn tại k sao cho $\overrightarrow a = k\overrightarrow b .$ $\vec{a} = k \vec{b} .$

Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng $\Leftrightarrow \overrightarrow {AB} = k\overrightarrow {AC} .$ $\Leftrightarrow \vec{A B} = k \vec{A C} .$

Chú ý: Cho hai vecto $\overrightarrow a$ $\vec{a}$ và $\overrightarrow b$ $\vec{b}$ không cùng phương. Với mỗi vecto $\overrightarrow c$ $\vec{c}$ luôn tồn tại duy nhất cặp số thực (m; n) sao cho $\overrightarrow c = m\,\overrightarrow a + n\,\overrightarrow b$ $\vec{c} = m \vec{a} + n \vec{b}$

Ví dụ: Cho tam giác ABC có trung tuyến AM. Gọi I là trung điểm của AM và K là điểm trên cạnh AC sao cho $AK = \frac{1}{3}AC$ $A K = \frac{1}{3} A C$ .

a) Tính $\overrightarrow {BI}$ $\vec{B I}$ theo $\overrightarrow {BA} , \overrightarrow {BC}$ $\vec{B A}, \vec{B C}$ .

b)Tính $\overrightarrow {BK}$ $\vec{B K}$ theo $\overrightarrow {BA} , \overrightarrow {BC}$ $\vec{B A}, \vec{B C}$ .

c) Chứng minh ba điểm B, I, K thẳng hàng.

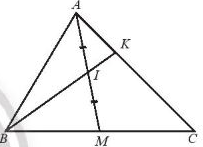
Giải

a) $\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} = \overrightarrow {BA} + \frac{1}{2}\overrightarrow {AM} = \overrightarrow {BA} + \frac{1}{2}\left( {\overrightarrow {BM} - \overrightarrow {BA} } \right) = \frac{1}{2}\overrightarrow {BA} + \frac{1}{4}\overrightarrow {BC}$ $\vec{B I} = \vec{B A} + \vec{A I} = \vec{B A} + \frac{1}{2} \vec{A M} = \vec{B A} + \frac{1}{2} (\vec{B M} - \vec{B A}) = \frac{1}{2} \vec{B A} + \frac{1}{4} \vec{B C}$ (1)

b) $\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{1}{3}\overrightarrow {AC} = \overrightarrow {BA} + \frac{1}{3}\left( {\overrightarrow {BC} - \overrightarrow {BA} } \right) = \frac{2}{3}\overrightarrow {BA} + \frac{1}{3}\overrightarrow {BC}$ $\vec{B K} = \vec{B A} + \vec{A K} = \vec{B A} + \frac{1}{3} \vec{A C} = \vec{B A} + \frac{1}{3} (\vec{B C} - \vec{B A}) = \frac{2}{3} \vec{B A} + \frac{1}{3} \vec{B C}$ (2)

c) Ta có:

$\begin{array}{l} \left( 1 \right) \Rightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} \\ \left( 2 \right) \Rightarrow 3\overrightarrow {BK} = 2\overrightarrow {BA} + \overrightarrow {BC} \end{array}$ $\begin{array}{l} (1) \Rightarrow 4 \vec{B I} = 2 \vec{B A} + \vec{B C} \\ (2) \Rightarrow 3 \vec{B K} = 2 \vec{B A} + \vec{B C} \end{array}$

Nên $\overrightarrow {BI} = \frac{3}{4}\overrightarrow {BK}$ $\vec{B I} = \frac{3}{4} \vec{B K}$ (3)

Từ (3) suy ra ba điểm B, I, K thẳng hàng

B. Bài tập minh họa

Câu 1: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG}$ $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Hướng dẫn giải

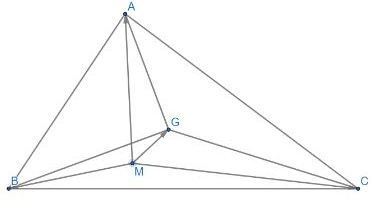
$\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \Leftrightarrow \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} = 3\overrightarrow {MG}$ $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G} \Leftrightarrow \vec{M G} + \vec{G A} + \vec{M G} + \vec{G B} + \vec{M G} + \vec{G C} = 3 \vec{M G}$

$\Leftrightarrow \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} } \right) + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = 3\overrightarrow {MG}$ $\Leftrightarrow (\vec{M G} + \vec{M G} + \vec{M G}) + (\vec{G A} + \vec{G B} + \vec{G C}) = 3 \vec{M G}$

$\Leftrightarrow 3\overrightarrow {MG} = 3\overrightarrow {MG} (đpcm)$ $\Leftrightarrow 3 \vec{M G} = 3 \vec{M G} (đ p c m)$ (Vì G là trọng tâm của tam giác ABC nên $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0)$ $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0})$

Câu 2: Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0$ $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$ . Chứng minh ba điểm I, G, J thẳng hàng

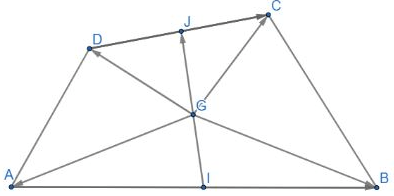
lý thuyết toán 10

Hướng dẫn giải

Ta có:

$\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {GI} + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JD} } \right) = \overrightarrow 0$ $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0} \Leftrightarrow (\vec{G I} + \vec{I A}) + (\vec{G I} + \vec{I B}) + (\vec{G J} + \vec{J C}) + (\vec{G J} + \vec{J D}) = \vec{0}$

$\\Leftrightarrow 2\overrightarrow {GI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ} + \left( {\overrightarrow {JC} + \overrightarrow {JD} } \right) = \overrightarrow 0$ $L e f t r i g h t a r r o w 2 \vec{G I} + (\vec{I A} + \vec{I B}) + 2 \vec{G J} + (\vec{J C} + \vec{J D}) = \vec{0}$

$\Leftrightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \Leftrightarrow 2\left( {\overrightarrow {GI} + \overrightarrow {GJ} } \right) = \overrightarrow 0$ $\Leftrightarrow 2 \vec{G I} + 2 \vec{G J} = \vec{0} \Leftrightarrow 2 (\vec{G I} + \vec{G J}) = \vec{0}$

$\Leftrightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \Rightarrow$ $\Leftrightarrow \vec{G I} + \vec{G J} = \vec{0} \Rightarrow$

G là trung điểm của đoạn thẳng IJ

Vậy I, G, J thẳng hàng

C. Trắc nghiệm Toán 10 bài 3

-----------------------------------------

Như vậy VnDoc đã giới thiệu các bạn tài liệu Lý thuyết Toán lớp 10 bài 3: Tích của một số với một vectơ CTST. Mời các bạn tham khảo thêm tài liệu: Giải bài tập Toán lớp 10, Chuyên đề Toán 10, Giải Vở BT Toán 10 , Toán 10 Cánh Diều, Toán 10 Kết nối tri thức, Tài liệu học tập lớp 10.

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

Bài trước

Bài sau

Chia sẻ bởi:
Lanh chanh

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!